What I am going to recount today is all well-known, and does not have anything to do with non-Hausdorff spaces. But it is something I learned about recently, and which I found nifty. Nothing I will say today is new, or even recent, except the fact that Hausdorffness is needed absolutely nowhere in what follows. In fact we will never need any sort of separation property.
Here is how I came to that. Since last time, Matthew de Brecht wrote and told me to have a look at some of Ruiyuan Chen‘s papers, and in particular [1]. One of these papers is (roughly) about extending the so-called López-Escobar theorem in (infinitary) logic. I won’t say what this is here. In order to understand it better, I decided to read R. Vaught’s famous paper [2], where he introduced what is now known as the Vaught transform B* of a subset B of a space with a Polish group action. That Vaught transform is very bizarre at first, and uses the notion of meagre set in a crucial way. Maybe I will talk about it later.
In the meantime, I would like to say that one of the key aspects of the Vaught transform is that B* is Borel as soon as B is. Proving this involves so-called sets with the Baire property, and I would like to explain what they are and how they explain a few things about Borel sets—but I will not explain Vaught’s work. The key is reasoning up to meagre sets, and realizing how much it gives you.
Borel sets
A σ-algebra on a set X is a family of subsets of X that is closed under countable unions and under complementation (hence also under countable intersections). This is a fundamental notion in measure theory.
The Borel σ-algebra of a topological space X is the smallest σ-algebra that contains all the open sets.
Good. How big is that? For example, is every subset of X Borel, or are there non-Borel subsets? Start with the real line R.
Well, there are non-Borel subsets of R, but if you have tried to prove it by yourself (and you haven’t been taught how to prove it yet), you may have experienced some difficulties. You may have realized that working with σ-algebras is hard. For example, you cannot assume that Borel sets are some form of countable union of countable intersections of open sets (that is simply untrue).
If you already know, there is something called Vitali sets, which cannot be Borel, but showing that requires one to work with Lebesgue measure on R. Oxtoby [3] manages to do without it, and does it with a notion of null sets that he defines directly. Showing the existence of Vitali sets crucially relies on the axiom of choice, which is fine since we use it all the time in topology anyway. (But we cannot prove that any non-Borel subset of R exists in ordinary Zermelo-Fraenkel set theory without the axiom of choice…)
The book [3] by Oxtoby, by the way, is an excellent reference on several things I will say, starting with the property of Baire. It is very readable, and usually sacrifices generality for clarity, which is a very good thing when you learn something new.
The property of Baire
Before I start, let me just say that there are too many things named after René-Louis Baire. We have:
- Baire spaces: topological spaces such that every intersection of a countable family of dense open sets is again dense;
- the Baire space (Example 4.8.12, and mentioned in several other places in the book) NN, the product of a countably infinite number of copies of N, where N has the discrete topology; at least the Baire space is a Baire space (Example 7.6.9 in the book);
- Baire sets in a topological space X: there are several inequivalent definitions, but the most common one equates them with elements of the smallest σ-algebra that contains all the compact Gδ subsets of X; all Baire sets are Borel, because all Gδ subsets are Borel;
- sets with the Baire property, in a topological space X: I will define them and study them below; in particular we will see that every Borel set has the Baire property.
All those notions are different, so please pay attention! We will only be interested in sets with the Baire property here. That should make things easier.
Let us fix a topological space X once and for all. From now on, when I say “set”, I will really mean “subset of X“.
The Baire property is very strange. A set is nowhere dense if and only if its closure has empty interior, or equivalently, if it is included in some closed set with empty interior. A meagre set is a set that is included inside a countable union of nowhere dense sets. That is a notion of smallness: we believe that a closed set with empty interior is small, and that countable unions of small sets are small.
In a Baire space, every meagre set M is indeed small, in the following sense: the complement of M contains a countable intersection of dense open sets, and is therefore dense. In other words, every meagre set has empty interior (… in a Baire space).
You probably know that by heart—that is very standard topology. In the introduction, I said that what I would talk about today would have nothing to do with non-Hausdorff spaces per se. Worse, the notion of meagre set is almost useless in dcpos—an admittedly interesting class of non-Hausdorff spaces. The reason is that density is almost useless in dcpos. Indeed, because every non-empty Scott-open subset contains a maximal element of the dcpo (by Zorn’s Lemma), its set of maximal elements is automatically dense. Hence any countable union of closed subsets that does not contain a maximal element is automatically meagre. For example, in the powerset P(N), with the Scott topology of inclusion, the family of all proper subsets of N (proper meaning different from N itself) is meagre, although it is far from being intuitively small, since it contains every point in the space except one.
But at least whatever I will say works in every topological space, not just Hausdorff spaces. (To be fair, I will need second countability near the end.)
Anyway, here is the definition. Let me write A Δ B for the symmetric difference of A and B, namely the set of points that are in A or in B, but not both. The operation Δ is associative, commutative, etc., and is in fact a group operation where every set A is its own inverse. (A short way of seeing that is to equate sets with their characteristic functions, and to realize that Δ is, pointwise, addition modulo 2.)
Definition. A set with the property of Baire is the symmetric difference U Δ M of an open set U and a meagre set M.
I will sometimes say that a set has the property of Baire if and only if it is open modulo a meagre set.
A key observation is that the boundary ∂U of any open set U is nowhere dense. (In general, the boundary of a set A is ∂A = cl(A)–int(A). Beware that this fails if we do not assume U open: the boundary of Q in R is the whole of R.) This is shown as follows. Since U is open, ∂U = cl(U)–U. Now imagine any open subset V of ∂U. Since V is disjoint from U, it is included in its complement Uc, and therefore also in the interior int(Uc) of the latter, which happens to be equal to the complement of cl(U). Since V is included in cl(U) (being included in ∂U ⊆ cl(U)), and also in its complement, V is empty.
It follows:
Lemma 1. The complement of a set with the property of Baire has the property of Baire. The sets with the property of Baire are also the closed sets modulo meagre sets.
Proof. Let A be equal to some open set U modulo some meagre set M. Then Ac is equal to Uc Δ M. This is because, for every set B, Bc = X Δ B: then Ac = X Δ (U Δ M) = (X Δ U) Δ M = Uc Δ M, using the associativity of Δ.
Next, Uc is equal to the disjoint union of int(Uc) and of ∂U, hence to int(Uc) Δ ∂U. We again use the fact that Δ is associative: Ac is equal to int(Uc) Δ (∂U Δ M), and we observe that U’=int(Uc) is open and M’=∂U Δ M is meagre, because it is included in the union of the nowhere dense set ∂U and the meagre set M.
For the second part, we take the complement of the latter formula: A is equal to the complement of U‘ Δ M’, and that is equal to U‘c Δ M‘, a closed set modulo a meagre set. ☐
Lemma 2. Every countable union of sets with the property of Baire has the property of Baire.
Proof. Let us consider countably many sets Bn = Un Δ Mn, with Un open and Mn meagre. We take the union B of the sets Bn, U of the sets Un, M of the sets Mn. We claim that B is equal to U modulo some set M’ included in M. (Hence M’ is meagre, and this will finish the proof.)
M‘ is necessarily equal to B Δ U (because Δ is a group operation where every element is its own inverse), namely to the union of B–U and of U–B. Every point of B that is not in U is in some Bn = Un Δ Mn but in no Un, hence in some Mn, hence in M. Every point of U that is not in B is in some Un, but not in Bn = Un Δ Mn, hence it must also be in Mn, hence in M. Hence, indeed, M’ included in M, and we are done. ☐
Those two lemmas entail that:
Proposition. The family of sets with the property of Baire form a σ-algebra.
That σ-algebra contains all the open sets (… because the empty set is meagre), so it is larger than the smallest σ-algebra that contains all the open sets, namely the Borel σ-algebra. It follows:
Proposition. Every Borel set has the property of Baire. ☐
Borel sets are somehow unfathomable. If you have already tried to work with them, you know that you need fancy tools such as the monotone class lemma (a.k.a., the λπ-theorem), or specific ordinal inductions, so as to prove anything valuable about Borel sets, more often than not.
Sets with the property of Baire look much simpler: just open (or closed) sets, modulo some meagre set. I am tempted to think that this shows that Borel sets, having the property of Baire, cannot be completely pathological. Or maybe that shows that sets with the property of Baire can be terribly complex… depends on your personal mood, I would say!
Anyway, I have decided to be optimistic today: Borel sets are simple! up to some small (=meagre) set, every Borel set is open (or closed).
Baire regularization
However, in second-countable spaces, sets with the property of Baire are also as complicated as any set, still modulo meagre sets, as I will now argue. The argument is something that I will call Baire regularization (I don’t know whether it already has a name).
Henceforth let me assume that X is second-countable, and that U0, U1, … is a countable base of its topology. For every set A, let AΔ be the union of all the sets Un in the given base such that Un–A is meagre. That is a kind of interior of A modulo meagre sets: instead of taking the union of the sets Un that are included in A, we take them in also if they go a bit beyond A, by a meagre amount.
Let also A* be the complement of (Ac)Δ; explicitly, A* is the intersection of all the complements of the sets Un such that Un ∩ A is meagre, but I do not think that will help you. Since the closure of A is the complement of the interior of Ac, one may think of A* as a kind of closure of A modulo meagre sets.
By the way, Vaught uses the same notations for different notions. But those are related: the key is the same in each case, namely defining variants on some well-known notions (interior, closure, here), up to meagre sets.
We have:
- AΔ is open, since it is a union of open sets.
- AΔ–A is meagre: indeed, it is the union of those sets Un–A that are meagre, and any countable union of meagre sets is meagre. (This is where we need X to be second-countable.)
- Replacing A by its complement Ac, we obtain that (Ac)Δ – Ac is meagre. Hence A–A* = A ∩ (Ac)Δ = (Ac)Δ – Ac is meagre.
- Since (Ac)Δ is open (see first bullet above, replacing A by Ac), A* is closed.
- The Baire regularization B(A) of A is A ∪ A*. This is also equal to A* ∪ (A–A*), which is the union of a closed set and a meagre set. This is a disjoint union, hence also equal to the symmetric difference A* Δ (A–A*). That exhibits B(A) as a set with the property of Baire (see our first lemma; or use the fact that such sets form a σ-algebra).
The next property is more difficult to observe, and says that B(A) is the smallest Baire superset of A “up to meagre sets”.
Lemma 3. Let X be a second-countable space, and A be an arbitrary subset of X.
- B(A) is a set with the property of Baire containing A,
- every subset of B(A)–A with the property of Baire is actually meagre,
- in particular, any superset E of A with the Baire property contains B(A) up to some meagre set.
Proof. Let again U0, U1, … be a countable base of the topology of X. We already know that B(A) is a set with the property of Baire containing A (item 1). We will show item 2. That will imply item 3, since B(A)–E will be a subset of B(A)–A with the property of Baire, hence will be meagre.
Let us consider a subset of B(A)–A with the Baire property, say U Δ M, where U is open and M is meagre. In particular, U is included in (B(A)–A) ∪ M. It follows that U ∩ A is included in M, hence is meagre. U is a union of sets of the form Un, and each one is such that Un ∩ A, being included in U ∩ A, is meagre. Now we look at (Ac)Δ: this is the union of all the sets Un such that Un – Ac = Un ∩ A is meagre, and therefore (Ac)Δ contains U.
Taking complements again, U cannot intersect the complement A* of (Ac)Δ.
We consider any point x of U. Since U is included in (B(A)–A) ∪ M, x is in M or in B(A)–A. However, in the second case, x is in B(A) = A ∪ A* but not in A, and we have just seen that x cannot be in A* either, since it is in U, which does not intersect A*. So x must be in M.
In summary, we have shown that U is included in M. It follows that our original set U Δ M is equal to M – U, which is included in the meagre set M, hence is meagre as well. ☐
Souslin’s A-operation
We all make mistakes, and it is sometimes comforting to hear that great mathematicians have made some. Apparently, Lebesgue made a famous one once, and claimed that the image f[A] of a Borel set A by a continuous map f is Borel. This is wrong, and understanding the phenomenon that occurs here led Souslin and Lusin to the definition of analytic sets, to the Lusin separation theorem, and so on; this was the start of descriptive set theory.
This is not a course on descriptive set theory (about which I know almost nothing, anyway), so I will just throw in a few definitions and gratuitous claims, then I will proceed to what I want to talk about, Souslin’s A-operation.
An A-set is the image f[A] of a Borel set A by a continuous map f from a Polish space X to some topological space Y. If Y is Polish, then A-sets are called analytic sets. All Borel sets are analytic, and an analytic set whose complement is analytic is Borel, but there are in general analytic sets that are not Borel (notably, in Baire space), by a theorem due to Robert Solovay. A-sets are closed under countable unions, countable intersections, images by Borel maps… and under the so-called A-operation of Souslin.
In order to describe the A-operation, we need to picture Baire space NN as a tree, as follows. We start with the root of the tree, which we call ε. The symbol ε also denotes the empty string, and that is deliberate. Below ε, we create countably many new (level 1) vertices 0, 1, 2, 3, etc. Below each vertex n thus created, we create countably many new (level 2) vertices n0, n1, n2, etc. Below each level 2 vertex mn, we create countably many new (level 3) vertices mn0, mn1, mn2, etc. And we continue forever, see the picture below.
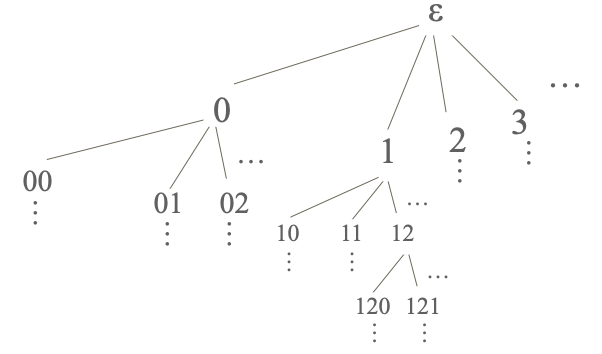
More succinctly, the vertices of this tree are simply the finite sequences of natural numbers, and a vertex is above another one if and only if it is a prefix of the second one. The (infinite) branches of this tree (starting from the root) can be equated with infinite sequences of natural numbers, e.g., going through ε, 1, 12, 121, etc., yields the infinite sequence 121… Hence Baire space is simply the space of all infinite branches through this tree.
Now let N* be the set of all finite sequences of natural numbers. Those naturally describe unique vertices in the tree (e.g., 11 or 121).
A Souslin scheme (over a σ-algebra) is a map from N* to elements of the σ-algebra. In other words, it is a way of decorating each vertex w in the tree above with an element of the σ-algebra, Aw.
The A-operation consists in reading that tree as an expression where we combine the various sets Aw, w ∈ N*, by taking intersections when traveling vertically in the tree, and by taking unions horizontally.
More precisely, for each branch s in NN, we compute an element As of the σ-algebra by taking the intersection of all the sets Aw, where w ranges over the vertices on the branch (i.e., the finite prefixes of s, seen as an infinite sequence).
Then we compute the union of all the sets As, when s ranges over the branches in NN. I will call that the value of the Souslin scheme.
But, ah… this is an uncountable union, and therefore we do not know whether the resulting set is still in the σ-algebra. If we take the σ-algebra of Borel subsets of Baire space, there are cases where this gives us a set outside the σ-algebra, by Solovay’s theorem.
Funnily, that problem does not occur with the σ-algebra of sets with the property of Baire, as we will now see. This is a theorem due to Otto Marcin Nikodým, the same one as in the Radon-Nikodým(-Lebesgue) theorem about existence of densities for pairs of absolutely continuous measures. The proof I am giving below is from course notes by Christian Rosendal [4]. (Beware that he implicitly assumes his topological space to be at least second-countable, otherwise “the largest open set in which ∼ D is comeagre” of his Example 2 may fail to exist.)
Before we do this, a few remarks:
- There is another way to give a value to a Souslin scheme, which may appear to be more natural to functional programmers out there. We define it by recursion over the tree by positing that the value aw of the subtree rooted at any vertex w ∈ N* is equal to the union of the values awn of each of the subtrees rooted at its immediate children wn (i.e., the list of numbers from w followed by the number n), n ∈ N, intersected with the set Aw that decorates w.
Let me say that this is the wrong way. It appears natural, but there is something fishy here: we will always get an element from the original σ-algebra here (provided we can make sense of such a non-terminating recursion), because we are only using countable unions and intersections. In particular, the value aε at the root does not give you the intended value vε of the Souslin scheme. - We can always assume that we start from a regular Souslin scheme, namely one in which the values Aw decrease (not necessarily strictly) when you go down any branch. To see that, replace Aw by the intersection of all the sets that decorate vertices on the finite path from the root ε to w (i.e., those indexed by the prefixes of w).
Nikodým’s theorem
Let us assume a regular Souslin scheme over the σ-algebra of sets with the property of Baire, in a second-countable topological space X. For short, let me say “measurable” instead of “set with the property of Baire”.
Lemma 3 above implies the following:
Fact A. For every set A, and every measurable subset B of B(A)–A, all the subsets of B are measurable.
This would fail if “measurable” meant “Borel set”. The proof is as follows. Since B is a measurable subset of B(A)–A, Lemma 3 tells us that B is meagre. Every subset of a meagre set is meagre, and all meagre sets are measurable (i.e., have the property of Baire).
This being made clear, we define a new Souslin scheme by: A’w = B(vw) ∩ Aw, where vw is the value of the subtree rooted at any vertex w ∈ N* in the original Souslin scheme. That is, vw is the union, over all branches starting from w and going down, of the intersection of the sets decorating the vertices on that branch. Then we regularize vw, and we take the intersection with Aw. The latter is simply meant to ensure that A’w is included in Aw. The important operation is regularizing vw. By Fact A, all the subsets of any measurable subset of A’w–vw (⊆ B(vw)–vw) are measurable.
For each vertex w, let the error term Ew be equal to A’w minus the union of the sets A’wn, n ∈ N. Ew is measurable, but that is not the important point. Ew is included in A’w minus the union of the sets A’wn, n ∈ N. The latter union contains the union of the sets vwn ∩ Awn = vwn, n ∈ N, because each B(vwn) contains vwn, and that union is simply the value vw (because our original Souslin scheme is regular). Hence Ew is included in A’w–vw, and therefore (using Fact A), every subset of Ew is measurable.
Let E be the union of all the sets Ew, w ∈ N*. Contrarily to NN, N* is countable. Therefore every subset of E, which can be expressed as the union of countably many subsets, one subset of each Ew, w ∈ N*, is measurable.
For every w ∈ N*, A’w – E is included in the union of the sets A’wn – E, n ∈ N. Indeed, let x be a point of A’w – E. In particular, x is not in Ew, and since it is in A’w, it must be in A’wn for some n ∈ N, by the definition of Ew.
Let us iterate this construction. We start from any point x in A’ε – E. That is in the union of the sets A’n – E, n ∈ N, hence it is in some set A’n[0] – E, for some natural number n[0]. Taking w=n[0], we repeat the argument: A’n[0]– E is included in the union of the sets A’n[0]n– E, n ∈ N. Therefore there is a natural number n[1] such that x is in A’n[0]n[1]– E. Then there is a third natural number n[2] such that x is in A’n[0]n[1]n[2]– E, and so on. We proceed in the same way, defining an infinite sequence s = n[0], n[1], n[2], …, n[k], …, such that x is in A’n[0]n[1]n[2]…n[k]– E for every k in N.
In particular, x is in An[0]n[1]n[2]…n[k]– E for every k in N, hence it lies in the intersection of the measurable sets encountered on the branch s in the original (regular) Souslin scheme. In particular, x is in the union of those intersections, which happens to be the value vε of the original Souslin scheme, minus E. Since x is an arbitrary point in A’ε – E, we obtain that A’ε – E is included in vε – E.
Now we note that A’ε = B(vε) ∩ Aε is measurable, hence A’ε – E is also measurable. It is included in vε, so vε is equal to the union of the measurable set A’ε – E with some subset of E. But every subset of E is measurable! Therefore vε is measurable.
We can now conclude:
Theorem (O.M. Nikodým). Let X be a second-countable space. The σ-algebra of those subsets of X that have the property of Baire is closed under Souslin’s A-operation. In particular, every A-set in X has the property of Baire.
The proof does not use much from the property of Baire: just that Fact A holds. This lends itself to a natural generalization, which I will let you discover (Theorem 4 in [4]): every σ-algebra that “admits covers” (i.e., satisfying Fact A) is closed under Souslin’s A-operation. This is apparently due to Szpilrajn-Marczewski.
Remarkably, Nikodým’s theorem is usually proved when X is a Polish space. As we have seen, it holds in any second-countable space whatsoever, including many kinds of non-Hausdorff spaces (and certainly quasi-Polish spaces, in particular).
- Ruiyuan Chen. Borel functors, interpretations, and strong conceptual completeness for Lω1ω. Transactions of the AMS 372(12), pages 8955-8983, 2019.
- Robert Lawson Vaught. Invariant sets in topology and logic. Fundamenta Mathematicae 82.3, pages 269-294, 1974.
- John C. Oxtoby. Measure and category. Springer Graduate Texts in Mathematics, 2nd edition, 1980.
- Christian Rosendal. A closure property for the Souslin operation. Course notes, spring 2012.

— Jean Goubault-Larrecq (January 20th, 2020)
