I have talked in a post dated November 20th, 2022 about weakly Hausdorff spaces and locally strongly sober spaces. A space is locally strongly sober if and only if for every ultrafilter U, lim U is empty or is the closure ↓z of a unique point z. A strongly sober space is one where lim U is the closure ↓z of a unique point z, for every ultrafilter U. In other words, where every ultrafilter has a unique largest limit.
Douglas Hoover examined a very close notion in 1995 [1]: spaces where every net (xi)i ∈ I, ⊑ has either no limit at all, or a unique largest limit. He called them maximal limit spaces.
This must also be compared with Theorem 8.2.29 in the book: the spaces in which every self-convergent net have a unique largest limit are exactly the sober spaces. (A net is self-convergent if and only if it converges to every of its elements.)
Hence some comparison of the notions is in order: all of those notions look at a specific class of nets, or of filters (the ultrafilters, the nets, the convergent nets) and specify that they should have a unique largest limit. Is there any relationship between them? In this post, I will concentrate on maximal limit spaces, and on weakly Hausdorff spaces.
Maximal limit space ⇒ locally strongly sober
A first class of examples of maximal limit spaces is given by the Hausdorff spaces: in a Hausdorff space, every net either has no limit or a unique limit (Proposition 4.7.4 in the book). At the end of this post, we will see that every bc-domain X is a maximal limit space in its Scott topology. But that is more complicated, and we do not have the tools yet to prove this.
For now, we observe that being a maximal limit space is a pretty strong requirement. In Proposition A below, which is part of the implication (i)⇒(ii) of Theorem 3.3 of [1], we will see that every maximal limit space has to be locally strongly sober. Well, Hoover uses “supersober” instead of “locally strongly sober”, but that means the same thing.
I will also deal with strong sobriety (without “locally”). To this end, let me call space possibly pointed if and only if every net converges in that space. Hence a strongly sober space is the same thing as a locally strongly sober space that is possibly pointed. The name “possibly pointed” may sound strange; we will see later that they are exactly the spaces that are either empty or pointed, where pointed means having a least element in their specialization preordering.
Proposition A.
- A space X is a maximal limit space if and only if every proper filter has a unique largest limit, or no limit at all.
- X is a possibly pointed space if and only if every proper filter has a limit.
- In particular, every maximal limit space X is locally strongly sober, and every possibly pointed maximal limit space is strongly sober.
Before we start proving that, we note that there are maximal limit spaces that are not possibly pointed. Consider a Hausdorff, non-compact space X (for example, the real line). This cannot be strongly sober, because a strongly sober space is compact. However, every Hausdorff space is a maximal limit space, as we have seen.
Proof. The first two parts of the lemma follows from a well-known correspondence between convergence of nets and convergence of filters, which I am going to spell out now.
Given a net (xi)i ∈ I, ⊑, we can form its filter F of sections: a subset A of X is in F if and only if the net is eventually in A, namely if and only if xi is in A for i large enough. (This is always a proper filter.) Then the limits of (xi)i ∈ I, ⊑ are exactly the limits of F: a point x is a limit of (xi)i ∈ I, ⊑ if and only if every open neighborhood of x contains xi for i large enough, and x is a limit of F if and only if every open neighborhood of x is in F.
It follows that if every proper filter has a unique largest limit or none at all, then the filter of sections of any net has a unique largest limit or none at all, so every net has a unique largest limit or none at all, namely X is a maximal limit space. Similarly, if every proper filter has a limit, then the filter of sections of any net has a limit, so every net has a limit, and therefore X is possibly pointed.
In the converse direction, given a proper filter F, we form a net as follows. Let I be the set of pairs (x, U) where U is an open subset of X inside F and x ∈ U, and let us preorder it by (x, U) ⊑ (y, V) if and only if V ⊆ U. The set I is directed: it is non-empty because X in in F, and X contains a point x since F is proper (X cannot be empty), so (x, X) is in I; given (x, U) and (y, V) in I, U ∩ V is in F, hence non-empty, so it contains a point z, and then (z, U ∩ V) is larger than or equal to (x, U) and (y, V) with respect to ⊑. We then form the net (zx,U)(x, U) ∈ I, ⊑, where zx,U≝x, and we check that it has the same limits as F.
- If z is a limit of (zx,U)(x, U) ∈ I, ⊑, then every open neighborhood W of z contains zx,U (= x) for (x, U) ∈ I large enough. We pick one, (x, U): W contains zy,V for every pair (y, V) in I such that (x, U) ⊑ (y, V). In particular, it contains zy,U (= y) for every y ∈ U, so W ⊇ U. Since U is in F, W is in F, too. We have shown that every open neighborhood W of z is in F, so z is a limit of F.
- If z is a limit of F, then every open neighborhood W of z is in F. By definition of I, (z, W) is then in I. For every (y, V) in I such that (z, W) ⊑ (y, V), we have V ⊆ W by definition of ⊑, so zy,V, which is equal to y, hence in V, is also in W. We have just shown that zy,V is in W for large enough (y, V), so z is a limit of (zx,U)(x, U) ∈ I, ⊑.
It follows that if X is a maximal limit space, then for every proper filter F, the associated net (zx,U)(x, U) ∈ I, ⊑ has a unique largest limit or no limit at all, hence so does F. Similarly, if X is possibly pointed, then for every proper filter F, the associated net (zx,U)(x, U) ∈ I, ⊑ has a limit, so F has a limit, too.
The final part of the Proposition follows from the first two, since every ultrafilter is a proper filter. ☐
A space X is weakly Hausdorff in the sense of Klaus Keimel and Jimmie Lawson [2] if and only if for any two points x and y in X, for every open neighborhood W of ↑x ∩ ↑y, there is an open neighborhood U of x and there is an open neighborhood V of y such that U ∩ V ⊆ W. See the following picture, which I have already used in the previously mentioned post.
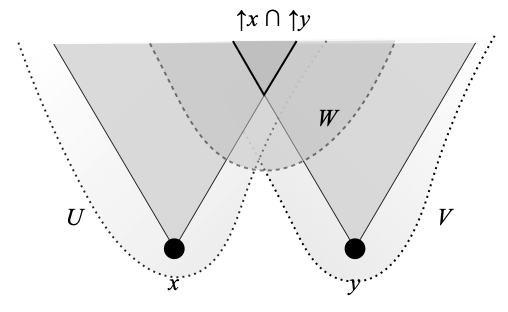
In this post, I had proved that a space is locally strongly sober if and only if it is weakly Hausdorff, coherent, and sober. (A space is coherent if and only if the intersection of any two compact saturated subsets if compact (saturated). For sober spaces, see Section 8.2 of the book.)
Hence every maximal limit space is weakly Hausdorff, coherent, and sober.
The various meanings of “weakly Hausdorff”, and continuous maxima
Now, if you read [1], a bit of warning about the vocabulary. Hoover has a different notion of weakly Hausdorff spaces: a space is weakly Hausdorff in Hoover’s sense if and only if any two points x and y with no common upper bound can be separated by disjoint open neighborhoods. This is the situation depicted in the picture above in the special case where ↑x ∩ ↑y is empty.
Hence a space that is weakly Hausdorff in Keimel and Lawson’s sense is weakly Hausdorff in Hoover’s sense, but the converse fails, as we now demonstrate. We will need to know that a monotone convergence space (Section 8.2.5) is a T0 topological space whose specialization ordering ≤ turns it into a dcpo, and whose open sets are all Scott-open with respect to ≤; every sober space is a monotone convergence space. (Hoover calls the latter DC-spaces, by the way.)
Example B. (A weakly Hausdorff space in Hoover’s sense, but not in Keimel and Lawson’s sense.) We consider any non-sober complete lattice L in its Scott topology. John Isbell was the first one to show that such a thing exists in 1982, and I gave a description of it in a post (April 20th, 2019). Just like every complete lattice, or even every bounded sup-semilattice, it is weakly Hausdorff in Hoover’s sense, for the trivial reason that ↑x ∩ ↑y is never empty. In [3, Example 4.10], I explained why L cannot be weakly Hausdorff (in Keimel and Lawson’s sense): as we have seen in the post on locally strongly sober spaces and weakly Hausdorff spaces, for a weakly Hausdorff space, monotone convergence and sobriety are equivalent properties. But any complete lattice, even any dcpo, in its Scott topology is a monotone convergence space, and L is not sober.
Now Hoover has another notion: a topological space X has continuous maxima if and only if the partial function ⊔, which maps any pair of points x, y that have a supremum to their supremum x ⊔ y, is continuous on its domain of definition dom ⊔, seen as a subspace of X × X, with the product topology. I don’t quite like the name, since it induces a confusion between maxima and suprema, but I will keep it nonetheless.
Lemma C. Let X be a topological space.
- If X is weakly Hausdorff (in Keimel and Lawson’s sense), then X is weakly Hausdorff (in Hoover’s sense) and has continuous maxima.
- If X is weakly Hausdorff (in Hoover’s sense), has continuous maxima, and any two points with an upper bound have a least upper bound, then it is weakly Hausdorff (in Keimel and Lawson’s sense).
Proof. 1. Let X be weakly Hausdorff in Keimel and Lawson’s sense. We have already seen that X is weakly Hausdorff in Hoover’s sense. Let (x, y) be any point in dom ⊔. We wish to show that given any open neighborhood W of x ⊔ y, there are open neighborhoods U of x and V of y such that for every point (x’, y’) in (U × V) ∩ dom ⊔, x’ ⊔ y’ is in W. Since x ⊔ y is in W, ↑(x ⊔ y) = ↑x ∩ ↑y is included in W. We take U and V as in the definition of weakly Hausdorff spaces (in the sense of Keimel and Lawson): for every point (x’, y’) in (U × V) ∩ dom ⊔, x’ ⊔ y’ is in U, since it lies above x’, which is in U, and it is in V, too, so it is in W.
2. Let us consider any two points x and y, and an open set W that contains ↑x ∩ ↑y. If ↑x ∩ ↑y is empty, then the fact that X is weakly Hausdorff in Hoover’s sense implies that x has an open neighborhood U, y has an open neighborhood V, and U and V are disjoint, in particular, U ∩ V ⊆ W. Otherwise, x and y have a common upper bound, and since we have assumed that any pair of points with an upper bound have a least upper bound, they must have a supremum x ⊔ y. Since X has continuous maxima, there are open neighborhoods U of x and V of y such that for every point (x’, y’) in (U × V) ∩ dom ⊔, x’ ⊔ y’ is in W. Hence, given any point z in U ∩ V, and using the fact that (z, z) is in (U × V) ∩ dom ⊔, we obtain that z is in W. Hence, once again, U ∩ V ⊆ W. ☐
There is no much point in keeping in mind all those different notions. In the sequel, “weakly Hausdorff” will always mean in Keimel and Lawson’s sense, and I will no longer mention continuous maxima. However, the property of having suprema as soon as you have upper bounds will be important.
Possibly pointed spaces and supercompactness
Let me return to the choice of “possibly pointed” to mean a space in which every net (or every proper filter) has a limit. I hesitated to call them “supercompact”, because this is really a strong form of compactness, and because the possibly pointed spaces are very much related to Heckmann and Keimel’s notion of supercompactness (see the February 2021 post).
More explicitly, a subset K of a topological space is supercompact in the sense of Heckmann and Keimel [4] if and only if every open cover (Ui)i ∈ I of K in X contains an element Ui such that K ⊆ Ui. As we have seen the aforementioned post, and as was shown by Heckmann and Keimel, the supercompact saturated subsets of X are exactly the upward closures ↑x of point x of X. This notion should not be confused with de Groot’s notion of supercompactness.
Lemma D. The following are equivalent for a topological space X:
- X is possibly pointed: every net (xi)i ∈ I, ⊑ in X has a limit in X;
- Every proper filter F in X has a limit in X;
- X is empty, or supercompact in the sense of Heckmann and Keimel;
- X is empty or has a least element (in the specialization preordering ≤ of X), namely is empty or pointed.
Proof. The equivalence of 1 and 2 is by Proposition A.
We show that 3 and 4 are equivalent. This is clear if X is empty, hence let us assume X non-empty. If X is supercompact (as a subset of itself), and since it is saturated, it is equal to ↑x for some point x of X. Then x is a least element of X. If X has a least element x, then X=↑x is supercompact.
We claim that 2 implies 4. For that, we consider the filter {X}. If X is empty, then 4 is vacuously true. Otherwise, {X} is a proper filter. Let x be a limit of that proper filter. Every open neighborhood of x must be in {X}, namely, X is the only open neighborhood of x. Then, for every point z in X, x≤z: for every open neighborhood U of x in X, U is equal to X and is therefore an open neighborhood of z. It follows that x is a least element of X.
Finally, we show that 4 implies 2. Again, this is clear if X is empty. Otherwise, let X have a least element x. Given any proper filter F in X, we claim that x is a limit of F: the only open neighborhood of x is X, and it must be in F by definition of filters. ☐
All right, back to maximal limit spaces!
Maximal limit space ⇒ bounded-sup-complete
Let me say that a poset, or a T0 topological space X, is sup-complete if and only if every non-empty subset has a least upper bound. It is bounded-sup-complete if and only if every non-empty subset with an upper bound has a least upper bound.
Instead of “bounded-sup-complete”, Hoover uses the term “bounded complete”. But “bounded complete” usually means that every subset, empty or not, with an upper bound, has a least upper bound. (I also defined “bounded-complete” in the book as meaning that any two elements with an upper bound have a least upper bound plus that there is a least element of the whole space, and that is yet another notion, which I will call binary bounded-sup-complete below. It is equivalent in a dcpo, or in a monotone convergence space. We have already encountered binary bounded-sup-completeness in Lemma C, item 2, although we did not say so then.)
The following is (also) part of the implication (i)⇒(ii) of Theorem 3.3 of [1].
Proposition E. Every maximal limit space X is bounded-sup-complete.
Proof. Before we start, X is locally strongly sober by Proposition A, hence sober, hence T0. Hence least upper bounds are unique, if they exist.
Let us fix a non-empty set S. Let S↑ denote the set of upper bounds of S, and let F be the collection of subsets A of X that contain S↑. It is easy to see that F is a filter. It is proper because S has an upper bound: so S↑ is non-empty, and therefore the empty set does not belong to F. By Proposition A, and since X is a maximal limit space, F must have a largest limit or no limit at all.
Let us investigate what the limits of F are. For every point y of X, y is a limit of F if and only if every open neighborhood U of y is in F, if and only if for every open neighborhood U of y, for every z ∈ S↑, U contains z, if and only if for every z ∈ S↑, for every open neighborhood U of y, U contains z, if and only if for every z ∈ S↑, y≤z. (We write ≤ for the specialization preordering of X.) Hence the limits of F are the lower bounds of S↑.
We observe that every element y of S is a lower bound of S↑. Indeed, by definition of S↑, every element z ∈ S↑ is above y.
In particular, this implies that every element of S is a limit of F. Since S is non-empty (this is where that assumption is used), F has a limit, by our previous characterization of limits of F. We know that F must have a largest limit or no limit at all, and we have just ruled out the second possibility. Therefore F has a largest limit. Let us call it x.
By our characterization of limits of F, x is the greatest lower bound of S↑. Since every element of S is a lower bound of S↑, every element of S is smaller than or equal to x: so x is an upper bound of S, and is therefore in S↑. This makes x the least element of S↑, namely the supremum of S. ☐
Before we go on, let me notice the following (well-known) fact, which shows that bounded-sup-completeness is a self-dual property; namely, X is bounded-sup-complete if and only if Xop is bounded-sup-complete.
Fact F. A poset (or a T0 topological space X) is bounded-sup-complete if and only if all its non-empty subsets with lower bounds have infima.
Indeed, if X is bounded complete and S is a non-empty subset with a lower bound, then its set S↓ of lower bounds is bounded and non-empty, hence has a least upper bound x. That least upper bound x is itself in S↓, because for every y in S, y is an upper bound of S↓, and therefore x≤y, by definition of x as a least upper bound. Hence x is the largest element of S↓, hence the infimum of S. The other direction follows by swapping lower and upper. And yes, this is very close to some of the arguments we have used in the proof of Proposition E.
We also note the following. We call binary bounded-sup-complete any T0 space in which any two points of X with an upper bound have a least upper bound. (Yes, I have said so already.)
Fact G. A T0 space X with suprema of directed families (e.g., a monotone convergence space, a sober space) is bounded-sup-complete if and only if it is binary bounded-sup-complete.
The ‘only if’ direction is trivial. For a proof of the ‘if’ direction, if any two points with an upper bound in X have a least upper bound, then any non-empty finite subset of X with an upper bound has a least upper bound, by taking binary suprema and iterating. Now, given any non-empty bounded set S, any of it non-empty finite subsets A is bounded, and then the directed family of suprema sup A, where A ranges over the non-empty finite subsets of S, is the supremum of S, as one easily checks.
Locally strongly sober + bounded-sup-complete ⇒ maximal limit space (and more)
The following is essentially the implication (iii)⇒(i) of Theorem 3.3 of [1].
Proposition H. Every binary bounded-sup-complete, weakly Hausdorff monotone convergence space X is a maximal limit space.
Proof. We consider a net (xi)i ∈ I, ⊑ in X, and we call L its set of limits. We also assume that L is non-empty, and we wish to show that L has a largest element. The ordering we consider is, as usual, the specialization ordering ≤ of X.
We start by showing that L is directed. Let us assume two elements x and y of L.
- We claim that x and y have an common upper bound. Otherwise, by using the weak Hausdorff property with W≝∅ (namely, the special case of weak Hausdorfness considered by Hoover), there are disjoint open neighborhoods U of x and V of y. Since x is a limit of (xi)i ∈ I, ⊑, every xi with i large enough is in U, and similarly with y, every xi with i large enough is in V. Since U and V are disjoint, this is impossible. (Explicitly: find i1 such that xi ∈ U for every i ⊒ i1 and i2 such that xi ∈ V for every i ⊒ i2; since I is directed, there is an index i in I above both i1 and i2, and then xi must be both in U and in V, which is impossible.)
- Hence x and y have a least upper bound x ⊔ y, since X is binary bounded-sup-complete.
- It remains to show that x ⊔ y is also a limit of (xi)i ∈ I, ⊑, and this will show that x ⊔ y is in L. Let us consider any open neighborhood W of x ⊔ y. Equivalently, W contains ↑(x ⊔ y) = ↑x ∩ ↑y. Since X is weakly Hausdorff, there is an open neighborhood U of x and an open neighborhood V of y such that U ∩ V ⊆ W. Since x is a limit of (xi)i ∈ I, ⊑, xi is in U for i large enough. Similarly, xi is in V for i large enough. Using U ∩ V ⊆ W (and the directedness of I), xi is in W for i large enough. We conclude that x ⊔ y is a limit of (xi)i ∈ I, ⊑ because W is an arbitrary open neighborhood of x ⊔ y.
Since X is a monotone convergence space, L has a supremum x. Also, every open neighborhood of x is Scott-open (with respect to ≤), hence contains some element of L.
The point x is a limit of (xi)i ∈ I, ⊑. The quick way to see that is that L, being a set of limits, is closed, and since X is a monotone convergence space, it is Scott-closed, hence contains the supremum of any directed family of elements of L, in particular of L itself. Explicitly, every open neighborhood U of x contains some element y of L, as we have seen above. But since y is a limit of (xi)i ∈ I, ⊑, this entails that xi must be in U for i large enough.
Finally, we have obtained that x is in L, and is the supremum of L, hence is the largest element of L, as desired. ☐
We summarize all our results in the following theorem, which is basically Theorem 3.3 of [1] (up to changes of denominations; also, the equivalence between 2 and 3 comes for free from the post on locally strongly sober spaces and weakly Hausdorff spaces that I have cited repeatedly here; finally, Hoover mentions coherence in Lemma 4.3 of [1]).
Theorem I. The following are equivalent for a topological space X:
- X is a maximal limit space;
- X is locally strongly sober and bounded-sup-complete;
- X is weakly Hausdorff, coherent, sober and bounded-sup-complete;
- X is a weakly Hausdorff, binary-bounded-sup-complete, monotone convergence space.
Adding possible pointedness to the mix, we have the following equivalence:
- X is a possibly pointed maximal limit space;
- X is strongly sober and bounded-complete (i.e., every bounded family, empty or not, has a supremum);
- X is weakly Hausdorff, possibly pointed, coherent, sober and bounded-complete;
- X is a weakly Hausdorff, possibly pointed, binary-bounded-sup-complete, monotone convergence space.
Bc-domains
It is now easy to show that every bc-domain in its Scott topology is a possibly pointed maximal limit space. A bc-domain is a continuous, pointed and binary-bounded-sup-complete dcpo (Definition 5.7.7 in the book). Being pointed, it is possibly pointed. (Yes, sometimes I fell the need to say something obvious.) Every bc-domain is stably compact (Fact 9.1.6 in the book), hence weakly Hausdorff (as we have seen in the post on weakly Hausdorff spaces) and sober, hence a monotone convergence space. Hence it satisfies the conditions of item 8 of Theorem I: every bc-domain is a possibly pointed maximal limit space, and in fact a stably compact one.
The converse fails: there are stably compact, possibly pointed maximal limit spaces that are not bc-domains with the Scott topology. For example, consider the lifting X⊥ of a non-empty compact Hausdorff space X without isolated points (say, [0, 1]). This is obtained by adding a fresh element ⊥ to X, and declaring that the open subsets of X⊥ are those of X, plus X⊥ itself. Since X is compact Hausdorff, it is stably compact, hence so is X⊥ (Proposition 9.1.10 in the book). Hence it is coherent and sober. Also, X⊥ is obviously possibly pointed, and it is binary bounded-sup-complete since any two elements that have an upper bound must either be equal, or one must be equal to ⊥. Hence, by Theorem I, item 8, X⊥ is a possibly pointed maximal limit space. But X⊥ does not have the Scott topology of its specialization ordering ≤, which puts ⊥ below every element, and makes every element of X incomparable, since the Scott topology would make every one-element set {x} with x in X open.
Every bc-domain is also a c-space (a space in which for every point x, every open neighborhood of x contains a point y such that x is in the interior of ↑y), and we have the following characterization. A pointed space is one with a least element, namely, a non-empty, possibly pointed space.
Proposition J. The bc-domains in their Scott topology are exactly the pointed maximal limit spaces that are at the same time c-spaces.
Proof. We have just seen that every bc-domain X is a possible pointed (even pointed) maximal limit space. Also, X is a continuous dcpo, hence a c-space in its Scott topology. More generally, the continuous dcpos with their Scott topology are exactly the sober c-spaces (Proposition 8.3.36 in the book). This allows us to prove the converse direction. Let X be a pointed maximal limit space that is also a c-space. Since every possibly pointed maximal limit space is strongly sober (Theorem I, item 6), hence sober, X is a continuous dcpo in its Scott topology. It is bounded-complete by Theorem I, item 6 again. Therefore X is a bc-domain. ☐
Next time
Next time, we will see a few additional properties of those spaces. One of the achievements of [1] is to show that for every locally compact space X, for every (possibly pointed) maximal limit space Y, the space [X → Y] of continuous maps from X to Y with the compact-open topology is a maximal limit space. Theorem I (or the equivalent that Hoover uses) is crucial for that result.
- Douglas N. Hoover. Maximal Limit Spaces, Powerspaces, and Scott Domains. Proceedings of the 11th International Conference on Mathematical Foundations of Programming Semantics (MFPS), New Orleans, Louisiana, USA. Electronic Notes in Theoretical Computer Science 1:253–272, 1995.
- Klaus Keimel and Jimmie Lawson. Measure extension theorems for T0-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
- Jean Goubault-Larrecq. On weakly Hausdorff spaces and locally strongly sober spaces. Topology Proceedings, 62:117–131, Oct. 2023, available as arXiv report 2211.10400.
- Reinhold Heckmann and Klaus Keimel. Quasi-continuous domains and the Smyth powerdomain. In Proceedings of the 29th Conference on the Mathematical Foundations of Programming Semantics, MFPS XXIX, New Orleans, Louisiana, USA, Dexter Kozen and Michael Mislove, editors, 2013. Electronic Notes in Theoretical Computer Science 298(4), pages 215-232, 2013.

— Jean Goubault-Larrecq (March 20st, 2024)
