This month I will focus on the structure of σ-algebras of certain spaces. Most prominently, the analytic spaces (a.k.a. Suslin spaces) are a class of spaces which include the Polish spaces, and they enjoy a certain number of pretty amazing properties. One of them is the following unique structure theorem: any two countable families F1 and F2 of Borel subsets of an analytic space X that separate the points of X generate the same σ-algebra. I will give a domain-theoretic proof of this. In fact, I will prove the more general positive unique structure theorem of F. Clerc, N. Fijalkow, B. Klin and P. Panangaden [1], and I will show that it holds on more general spaces than analytic spaces, and which I will call quasi-analytic spaces. They are to analytic spaces what quasi-Polish spaces [2] are to Polish spaces.
A bit of history
Before we start, let me say how I came to know this theorem. Prakash Panangaden was visiting France sometime in 2018 or 2019, and came to give a seminar at my lab, explaining the contents of [1]. He mentioned that the key to the whole construction was a mysterious positive unique structure theorem, and I was intrigued; Prakash then gave me a copy of the submitted version of his paper.
He also told us that the proof of the positive unique structure theorem was given to them by a Polish mathematician who preferred not to be named. I understood that the mathematician thought this was an utterly trivial result, which would tarnish his reputation if he was ever caught to have his name among the coauthors of a paper claiming to prove that result—but maybe he acted this way for other reasons, unknown to me. In any case, I will give credit to him. This is not a trivial result at all! (And maybe I will tarnish my own reputation by thinking that it is not trivial. 😕) If you wish to know who he is, well, read [1] carefully and you should be able to find out. Thanks to him, and thanks to Prakash for having introduced me to this wonderful result.
The domain-theoretic proof I am going to describe is a mere adaptation of the strategy of proof given in [1], which displays the role of certain dcpos explicitly. I found it shortly thereafter, and maybe Xiaodong Jia and Zhenchao Lyu, who were visiting my lab as postdocs at the time, still remember me explaining the argument to them during one or two of our weekly meetings.
σ-algebras and σ-lattices
A σ-algebra on a set X is a collection of subsets of X that is closed under complements and countable unions. In particular, it is closed under countable intersections as well. The notion of σ-algebra is a cornerstone of measure theory.
If you do not require closure under complements, you will get σ-lattices: precisely, a σ-lattice is a collection of subsets that is closed under countable unions and countable intersections. Given any family F of subsets of X, I will write L♭(F) for the σ-lattice generated by F. This is the smallest σ-lattice containing F. Non-constructively, this is defined as the intersection of all σ-lattices containing F, and this makes sense because every intersection of σ-lattices is a σ-lattice. More constructively, this is obtained by starting from F, forming all countable unions of sets obtained so far, then closing under countable intersections, then closing the result under countable unions again, then closing what we have obtained under countable intersections one more time, and so on, for transfinitely long.
You can do the same thing with σ-algebras. There is a smallest σ-algebra σ(F) containing F (the σ-algebra generated by F), which can be obtained either by taking the intersection of all σ-algebras containing F, or by closing under complements and countable unions for transfinitely long. A measurable space is a set X with a σ-algebra on X; the elements of the σ-algebra are called the measurable sets.
A σ-algebra is the same thing as a σ-lattice that is closed under complements. If F is already closed under complements, the constructive view on the construction of L♭(F) makes it easy to see that L♭(F) is not just any old σ-lattice, but is in fact a σ-algebra.
Given a topological space X, the σ-algebra σ(OX) generated by the collection OX of open subsets of X is by definition the Borel σ-algebra of X. Its elements are called the Borel subsets of X (or Borel measurable subsets).
Now, most of what I will do below is about comparing L♭(F) with another σ-lattice, which I will write as L#(F). In order to introduce it, I will need to talk about the specialization preordering ≤F of F. This is defined just like the specialization preordering of a topology: x ≤F y if and only if every set U in F that contains x also contains y.
Fact. F and L♭(F) have the same specialization preordering, namely ≤F.
Indeed, let us consider the collection Up of sets that are upwards-closed with respect to ≤F. Up contains F, and is clearly closed under countable unions and countable intersections (in fact under arbitrary unions and arbitrary intersections: that is just the Alexandroff topology of ≤F). By definition of L♭(F) as the smallest σ-lattice containing F, L♭(F) ⊆ Up. For any two points x and y such that x ≤F y, we have that every element U of Up that contains x contains y; therefore every element U of L♭(F) that contains x contains y, namely x ≤L♭(F) y. The converse fact that x ≤L♭(F) y implies x ≤F y is easy to see.
Let now X be any measurable space, and let me define L#(F) as the collection of measurable subsets of X that are upwards-closed with respect to ≤F. This is a σ-lattice, and L♭(F) ⊆ L#(F), since L♭(F) is the smallest σ-lattice containing F. Also, it is an easy exercise to show that the specialization preordering of L#(F) is ≤F.
The (positive) unique structure theorem—which I have not stated yet, I know, who would want to spoil the surprise!— will be a pretty simple consequence of a more general, and certainly at least as interesting theorem, which states that under pretty weak assumptions, the inclusion L♭(F) ⊆ L#(F) is in fact an equality. We are not ready for that, yet, though, and I need to tell you more about some of the wonderful properties of quasi-Polish spaces.
Quasi-Polish spaces
Quasi-Polish spaces are due to M. de Brecht, in his encyclopedic paper [2]. They have many equivalent definitions, and the one I will take is by using a few additional results from [3]: a quasi-Polish space is any space X that is homeomorphic to a Gδ subset of an ω-continuous dcpo. Let me (re)state some of the required definitions:
- a basis of a dcpo Y is a subset B of Y such that every point y in Y is the supremum of a directed family of elements of B, all way-below y;
- a continuous dcpo is a dcpo Y with a basis (and then Y itself can serve as a basis), and an ω-continuous is a dcpo with a countable basis;
- we will always consider dcpos with their Scott topology;
- a Gδ subset is the intersection ∩n∈N Vn of a chain of open subsets V0 ⊇ V1 ⊇ … ⊇ Vn ⊇ …, and we always consider it with the subspace topology.
It should be clear from this definition that every ω-continuous dcpo Y is a quasi-Polish space (take every Vn equal to Y). Every Polish space is quasi-Polish, too [1].
Enriching quasi-Polish topologies, part 1: adding a single closed set
Given any countable collection of Borel subsets of a Polish space X, we can enrich the topology of X so as to make all those Borel subsets clopen, while still guaranteeing that the resulting topology is Polish, and leaving the Borel σ-algebra unchanged. That is a remarkable result, which M. de Brecht extended to the realm of quasi-Polish spaces [1, Section 14].
Let me give the argument here. Let me write τ1 ⋁ τ2 for the join of two topologies τ1 and τ2, and τ ⋁ C for the join of τ and {∅, C, X} (the latter is the coarsest topology that contains C as open set). I will simply show that τ ⋁ C fits the bill. Let me also call a quasi-Polish topology any topology τ on X such that (X, τ) is quasi-Polish.
Lemma A. Let X be set, and τ be a quasi-Polish topology on X. For every closed subset C of (X, τ), τ ⋁ C is a quasi-Polish topology on X that contains τ, has C as open (hence clopen) set, and whose Borel σ-algebra is the same as that of τ.
Proof. Let U be the complement of C; U is open in X. The open subsets of τ ⋁ C are exactly the sets of the form V ∪ (W ∩ C), where V and W range over the open subsets of X; rewriting V as the union of V ∩ U and V ∩ C, and grouping V ∩ C together with W ∩ C, we see that, alternatively, the open subsets of τ ⋁ C are exactly the sets of the form (V ∩ U) ∪ (W ∩ C), where V and W range over the open subsets of X.
Up to homeomorphism, we write X as ∩n∈N Vn, where the sets Vn form an antitone sequence of open subsets of a continuous (resp., ω-continuous) dcpo Y. Let U be some open subset of Y such that U = U ∩ X (this exists by definition of the subspace topology, on X), and C be the complement of U in Y. We note that C ∩ X = C. The rest of the construction essentially consists in observing that both U and C are continuous (resp., ω-continuous) dcpos, in forming their disjoint union U+C, and finally in taking the subspace topology on X ⊆ U+C.
- U is a continuous (resp., ω-continuous) dcpo: in general, every Scott-open subset of a continuous (resp., ω-continuous) dcpo Y is itself a continuous (resp., ω-continuous) dcpo, and the Scott topology on the subset is also the subspace topology induced by the Scott topology on Y. This is well-known, but see Appendix A if you need a proof.
- C is a continuous (resp., ω-continuous) dcpo: similarly; see Appendix B in case of need.
- We form the (necessarily disjoint) union U+C. We equip it with the disjoint union ordering: x is below y in U+C if and only both x and y are in U, or both are in C, and x is below y in Y. This turns U+C into a dcpo, since directed families must be entirely included in U or in C; and that dcpo has a basis consisting of the union of a basis of U and a basis of C. Therefore U+C is a continuous (resp., ω-continuous) dcpo.
- The Scott-open subsets O of U+C are exactly the (disjoint) unions (V ∩ U) ∪ (W ∩ C) where V and W range over the Scott-open subsets of Y. Indeed, if O is Scott-open in U+C, then O ∩ U is Scott-open in U, and since the Scott topology on U is also the subspace topology induced by the inclusion in Y, O ∩ U = V ∩ U for some Scott-open subset V of Y; similarly, O ∩ C = W ∩ C for some Scott-open subset W of Y. Conversely, given any two Scott-open subsets V and W of Y, V ∩ U is Scott-open in U, and similarly W ∩ C is Scott-open in C; therefore (V ∩ U) ∪ (W ∩ C) is Scott-open in Y.
- It follows that the open subsets of the subspace topology on X induced by the inclusion in U+C are obtained by intersecting the above sets (V ∩ U) ∪ (W ∩ C) with X, and are therefore the set of the form (V ∩ U) ∪ (W ∩ C), where V and W range over the open subsets of X. We recognize the open sets in the topology τ ⋁ C. ☐
M. de Brecht showed that we can in fact add any Δ02 subset as a clopen subset to any quasi-Polish topology, with the same remaining constraints, but I will not need this. (And this allows me to forgo defining what a Δ02 subset is.) The proof is in fact easier than what I did above, provided you know that Π02 subspaces of quasi-Polish space are quasi-Polish—a deep fact that I did not want to rely upon so soon… although we will need it below. (I will also define Π02 subspaces there.)
Enriching quasi-Polish topologies, part 2: joins of quasi-Polish topologies
We will see that the lattice of quasi-Polish topologies on X is closed under joins of non-empty, countable families that are bounded from below. This, too, will be essential later.
To this end, we first show that quasi-Polish spaces are closed under countable topological products.
Proposition B. The topological product of any countable family (Xi)i ∈ I of quasi-Polish spaces is quasi-Polish.
Proof. For each i ∈ I, Xi is homeomorphic to a Gδ subset of a continuous dcpo Yi. Adding a bottom element to each Yi preserves all preexisting Scott-open sets, in the sense that any Scott-open subset of Yi is still Scott-open in Yi plus a fresh bottom element, below all elements of Yi. Hence, and without loss of generality, we may assume that each Yi has a least element. We equate Xi with ∩n∈N Vin, where the sets Vin, n ∈ N, form an antitone sequence of open subsets each Yi.
Since we have made sure that each Yi has a least element, their dcpo product Y ≝ Πi ∈ I Yi is a continuous dcpo (Proposition 5.1.56 in the book). Also, the Scott topology on Y coincides with the product of the Scott topologies. It follows that the topological product X ≝ Πi ∈ I Xi is a topological subspace of Y. Finally, X arises as the intersection of all the products Vin × Πj ∈ I, j≠i Yj (i.e., products of spaces of which only one is different from the whole dcpo Yj, and is Vin at position i), where i ranges over I and n ranges over N. Since I is countable, X is Gδ.
Since each Xi is quasi-Polish, we may assume that each Yi has a countable basis (and adding a bottom element only adds one elements to that basis). A basis of Y is given as the collection of tuples (yi)i ∈ I consisting of basis elements, and whose components are equal to bottom except for finitely many (this is also from Proposition 5.1.56 in the book). Such a basis is countable, so X is quasi-Polish. ☐
The following is Lemma 72 in [1], and I am just rephrasing M. de Brecht’s proof with my own definition of quasi-Polish spaces. This uses a difficult result, mentioned in this earlier post: every Π02 subspace of a quasi-Polish space (defined as Gδ subset of an ω-continuous dcpo, as before) is quasi-Polish. A Π02 subset of X is a countable intersection of UCO subsets, where a UCO subset (“union of closed and open”) of a topological space is a subset of the form U ⇒ V where U and V are open; the notation U ⇒ V stands for the set of points x such that if x ∈ U then x ∈ V. UCO subsets were mentioned in this post on countably presented locales, or in that post on sober subspaces and the Skula topology, and the name comes from R. Heckmann.
Lemma C. Let τ be a quasi-Polish topology on a set X, and (τi)i ∈ I be a non-empty, countable family of quasi-Polish topologies on X, all finer than τ. Then ⋁i ∈ I τi is also a quasi-Polish topology on X.
Proof. By Proposition B, the product Xω of the spaces (X, τi), where i ranges over I, is quasi-Polish. We form the diagonal Δ, namely the subset of elements of Xω whose components are all equal, and we observe that Δ is a Π02 subset of Xω. Here is how we prove it.
- Letting πi : Xω → (X, τi) be projection onto the ith factor, an element x of Xω is in Δ if and only if πi(x)≤πj(x) for all indices i, j in I, where ≤ is the specialization ordering of τ. (A quasi-Polish topology is always T0, since it arises as a subspace topology from the inclusion into a dcpo, whose Scott topology is T0.)
- A quasi-Polish topology on X, such as τ, is also second-countable, since it is generated by sets of the form ↟y ∩ X, where y ranges from a countable basis of the surrounding ω-continuous dcpo (from our definition of quasi-Polish spaces as Gδ subsets of ω-continuous dcpos). Let Un, n ∈ N, be a countable base of the topology τ. Then πi(x)≤πj(x) is equivalent to the fact that πi(x) ∈ Un implies πj(x) ∈ Un for every n ∈ N, namely to the fact that x belongs to the subsets πi–1(Un) ⇒ πj–1(Un) for every n ∈ N.
- We note that πi–1(Un) ⇒ πj–1(Un) is a UCO subset of Xω, because πi–1(Un) and πj–1(Un) are open in Xω. Indeed, πi is continuous from Xω to (X, τi), and τi is finer than τ, and similarly with πj.
- Hence Δ is the intersection of the countably many UCO subsets πi–1(Un) ⇒ πj–1(Un), where i and j range over I and n ranges over N.
We remember that any Π02 subspace of a quasi-Polish space is quasi-Polish. Therefore Δ is quasi-Polish. But Δ is homeomorphic to (X, ⋁i ∈ I τi), through the map that sends every point x of X to the constant tuple whose coordinates are all equal to x. ☐
Remark D. Under the assumptions of Lemma C, if (X, τi) has the same Borel subsets as (X, τ) for every i, then the Borel subsets of (X, ⋁i ∈ I τi) are also the same as those of (X, τ).
Indeed, this follows from the following two observations. First, τ is coarser than every τi, so every open subset of (X, τ) is Borel in τi, hence in ⋁i ∈ I τi; this means that the Borel σ-algebra of ⋁i ∈ I τi contains τ, hence also the Borel σ-algebra of τ, which is the smallest one with that property. Second, the open subsets of (X, ⋁i ∈ I τi) are countable unions of open sets, one from each τi. Indeed, this is true for the subbasic open subsets of (X, ⋁i ∈ I τi), which are simply open sets in one of the topologies τi; and this property is preserved under finite intersections and arbitrary unions. (In the latter case, consider any family of countable unions ∪i ∈ I Uji, where j ranges over some arbitrary set J, and where each Uji is open in τi. Their union is equal to ∪j ∈ J ∪i ∈ I Uji = ∪i ∈ I (∪j ∈ J Uji), and that is a countable union of sets ∪j ∈ J Uji, each of which being open in τi.) Any set that is open in any τi is Borel in τi, hence Borel in τ, since τi and τ have the same Borel σ-algebra. It follows that all the open subsets of (X, ⋁i ∈ I τi) are Borel subset of (X, τ): . Therefore the Borel σ-algebra of τ contains all the open subsets of (X, ⋁i ∈ I τi), hence also its Borel σ-algebra.
Enriching quasi-Polish topologies, part 3: making one Borel subset clopen
Given a Borel subset E (not just a closed subset C, as we did before) of a quasi-Polish space (X, τ), we might think of making it clopen by building τ ⋁ E ⋁ (X–E), but this fails: how would you prove that this is a quasi-Polish topology? Instead, we will add many more of open sets to the topology; the way this is done is by inducting on the way E is built as a Borel set using complements and countable unions.
Proposition E. For every quasi-Polish space X, for every Borel subset A of X, there is a finer quasi-Polish topology on X, with the same Borel subsets, in which A is open and closed.
Proof. Let us consider the collection Σ of Borel subsets A of X such that there is a finer quasi-Polish topology on X with the same Borel subsets, and in which A is open and closed. We claim that Σ is a σ-algebra that contains all the open sets of the original topology on X.
- Every open subset U of X is in Σ, namely: there is a finer quasi-Polish topology on X with the same Borel subsets in which U is open (… of course) and its complement C is open. This is just Lemma A.
- Let (An)n ∈ N be a countable collection of elements of Σ, and let us show that its union A is also in Σ. (Well, the notation enforces this collection to be non-empty. But, if you care about the empty collection as well, as one should, then note that the union of the empty collection is trivially in Σ.) For each n ∈ N, by induction hypothesis there is a quasi-Polish topology τn on X, which is finer than the original topology τ of X, makes An clopen, and has the same Borel subsets. We use Lemma C, and we obtain that ⋁n ∈ N τn is a quasi-Polish topology; it is clearly finer than τ, and A = ∪n ∈ N An is open in ⋁n ∈ N τn. Additionally, ⋁n ∈ N τn has the same Borel subsets as τ by Remark D.
A is open in ⋁n ∈ N τn, but we do not know whether it is closed; and there is no reason why it should be. However, by Lemma A the topology (⋁n ∈ N τn) ⋁ C, where C is the complement of A in X, is finer than ⋁n ∈ N τn, has the same Borel subsets, and makes C open, hence A closed. Therefore A is clopen in (⋁n ∈ N τn) ⋁ C, showing that A is indeed in Σ. - The complement of any set A in Σ is also in Σ: since A is in Σ, there is a finer quasi-Polish topology on X with the same Borel subsets, in which A is clopen; hence the complement of A is also clopen in that topology.
Therefore Σ is a σ-algebra. For every open subset U of the original topology OX on X, by Lemma A there is a quasi-Polish topology τ ⋁ C, where C is the complement of U, finer than τ, with the same Borel subsets as τ, and which makes C open, hence which makes A both open and closed. Therefore every open subset U of X is in Σ. This shows that Σ is a σ-algebra that contains all the open sets of the original topology on X, as I initially claimed.
In particular, Σ contains the Borel σ-algebra of X. But we have taken care to define Σ as a collection of Borel subsets of X. Hence Σ is exactly the Borel σ-algebra of X. Using the definition of Σ, we see that this means that for every Borel subset A of X (i.e., every element A of Σ), there is a finer quasi-Polish topology on X with the same Borel subsets, and in which A is open and closed. And that is exactly the statement of the Proposition. ☐
We go a bit further:
Proposition F. For every quasi-Polish space X, for every countable collection of Borel subsets An of X, n ∈ N, there is a finer quasi-Polish topology on X, with the same Borel subsets, in which every set An is open and closed.
Proof. This works for the empty collection as well, trivially. We will assume that the collection of subsets An is non-empty (which justified indexing them by N—there is no way of indexing an empty collection by N). By Proposition E, we can find quasi-Polish topologies τn, all finer than OX and with the same Borel σ-algebra, which make An clopen. By Lemma C, ⋁n ∈ N τn is a quasi-Polish topology, still with the same Borel σ-algebra (by Remark D), which makes all the countably many sets An clopen. ☐
Even better, consider any Borel measurable function f : X → R ∪ {–∞, +∞}. A generating family for the Borel σ-algebra on R ∪ {–∞, +∞} (whether you take the usual Hausdorff topology on the latter, or the Scott topology) is given by the half-open intervals ]q, +∞], where q ranges over the rational numbers. There are only countably many of them, and we have just seen that, if X is quasi-Polish, then we can enrich the topology of X to a topology τ that is still quasi-Polish, has the same Borel subsets, and in which every set f–1(]q, +∞]) is open. In other words, f is continuous from (X, τ) to R ∪ {–∞, +∞} with the Scott topology (namely, lower semicontinuous). Instead of just taking the half-open intervals ]q, +∞], we may consider those plus the open intervals ]q, q’[ where both q and q’ are rational. The same argument shows that there is a quasi-Polish topology on X, finer than the original topology on X but with the same Borel σ-algebra, such that f is continuous from (X, τ) to R ∪ {–∞, +∞} with its usual Hausdorff topology.
Finally, you can do exactly the same thing with countably many Borel measurable functions fn : X → R ∪ {–∞, +∞}: up to the enrichment of the topology of X to a finer quasi-Polish topology with the same Borel σ-algebra, we can make every fn continuous. I find that rather amazing.
But let us get back to our main theme: investigating when the inclusion L♭(F) ⊆ L#(F) is actually an equality.
Separating sets by σ-lattices
Given a family F of subsets of a set X, and two subsets A and B of X, we say that A is F-separated from B if and only if there is an element E of F that contains A and is disjoint from B. We also say that E separates A from B.
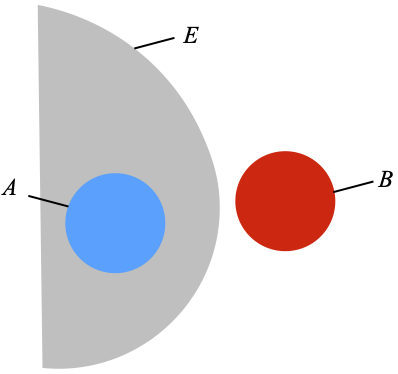
The main theorem of this post is really the following. Let me remind you that L♭(F) is the σ-lattice generated by F, that L#(F) is the σ-lattice of all Borel subsets of X that are upwards-closed with respect to ≤F, that ≤F is the specialization preordering of F, and that L♭(F) ⊆ L#(F).
Theorem G. Let X be a quasi-Polish space, and F be a countable family of Borel subsets of X. The following are equivalent for all Borel subsets A and B of X:
- A is L♭(F)-separated from B;
- A is L#(F)-separated from B;
- The upward closure ↑F A of A with respect to ≤F is disjoint from B.
Proof. 1 implies 2: if E separates A from B and is in L♭(F), then it is in L#(F). 2 implies 3: if E separates A from B and is in L#(F), then as E is upwards-closed with respect to ≤F, E also contains ↑F A, so ↑F A is also disjoint from B. The only challenge in proving the theorem lies in showing that 3 implies 1.
Hence we assume that 3 holds, but not 1, and we aim for a contradiction. Using Proposition F, we can assume that A, B, and all the (countably many) sets in F are both open and closed. Indeed, the change of topology implied in Proposition F preserves quasi-Polishness and Borel subsets. That is quite a simplification! But we worked hard, and we earned it.
By definition, X arises as a Gδ subset ∩n∈N Vn of some ω-continuous dcpo Y, where each Vn is Scott-open in Y. Let also B be a countable basis of Y. The key to the proof is the following claim: (∗) for all Scott-open subsets U and V of Y such that X ∩ U is not L♭(F)-separated from X ∩ V, there are elements y ∈ U ∩ B and z ∈ V ∩ B such that X ∩ ↟y is not L♭(F)-separated from X ∩ ↟z. (↟y denotes the set of points x such that y is way-below x in the continuous dcpo Y.) See the picture below, where ↟y and ↟z are shown as dashed (not dotted) lines.
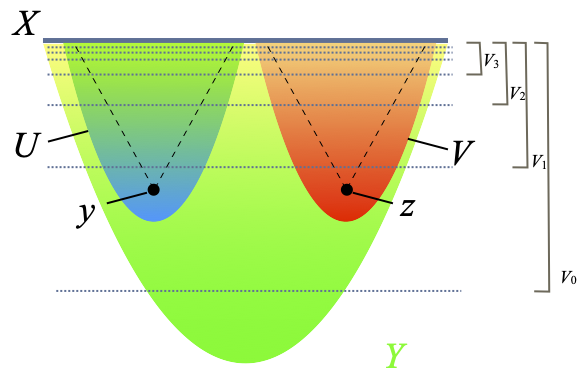
We prove (∗) by contraposition. We assume that, for all y ∈ U ∩ B and z ∈ V ∩ B, X ∩ ↟y is L♭(F)-separated from X ∩ ↟z by some set Eyz ∈ L♭(F). Let E ≝ ∪y ∈ U ∩ B ∩z ∈ V ∩ B Eyz. Since B is countable, this is a countable union of countable intersections of elements of L♭(F), so E is also in L♭(F). We claim that E separates X ∩ U from X ∩ V.
- We first check that E contains X ∩ U. For every element x of X ∩ U, since B is a basis of Y, x is the supremum of a directed family of elements y ∈ B way-below x, so one of them is in the Scott-open set U. Pick one. By assumption Eyz contains X ∩ ↟y for every z ∈ V ∩ B, so x is in Eyz for every z ∈ V ∩ B. Therefore x is in E.
- Second, we verify that E is disjoint from X ∩ V. Otherwise, let x be a point in E ∩ X ∩ V. Since x ∈ E, there is a point y ∈ U ∩ B such that x ∈ ∩z ∈ V ∩ B Eyz. Since x ∈ V, using the fact that B is basis, there is an element z ∈ V ∩ B way-below x and in V. We have x ∈ Eyz, but that is impossible since Eyz is disjoint from X ∩ ↟z by construction.
Since A and B are open in X (remember that they are in fact clopen, thanks to our use of Proposition F at the beginning of the proof), there are Scott-open subsets A and B of Y such that A = X ∩ A and B = X ∩ B. Using (∗), we build two monotone sequences (yn)n ∈ N and (zn)n ∈ N of elements of B such that:
- yn ∈ A ∩ Vn and zn ∈ B ∩ Vn
- X ∩ ↟yn is not L♭(F)-separated from X ∩ ↟zn.
This is by induction on n. When n=0, we use (∗) with U ≝ A ∩ V0 and V ≝ B ∩ V0, and we let y0 and z0 be the elements y and z that we obtain this way from (*). We can indeed use (*), because A = X ∩ A and B = X ∩ B, andA is not L♭(F)-separated from B, by our assumption that 1 fails. At step n+1, we use (*) with U ≝ ↟yn ∩ Vn+1 and V ≝ ↟zn ∩ Vn+1: by induction hypothesis X ∩ ↟yn is not L♭(F)-separated from X ∩ ↟zn, so neither is X ∩ U (=X ∩ ↟yn) from X ∩ V (=X ∩ ↟zn). Now (*) gives us two points y and z, which we rename as yn+1 and our zn+1 respectively.
Let y∞ ≝ supn∈N yn, z∞ ≝ supn∈N zn. Since yn ∈ A ∩ Vn for every n ∈ N and since every A ∩ Vn is upwards-closed, y∞ is in ∩n∈N (A ∩ Vn) = A ∩ X = A. Similarly, z∞ is in B.
We observe that y∞ ≰F z∞: otherwise, since y∞ is in A, z∞ would be in ↑F A, but z∞ is in B, and that would enforce that ↑F A is not disjoint from B, contrarily to item 3 of the the statement of the theorem, which have assumed. By definition of ≤F, there is an element W of F such that y∞ ∈ W and z∞ ∉ W. Since W is both open and closed in X (remember Proposition F: this allowed us to consider all the elements of F as being clopen), there are two Scott-open sets W and W’ of Y such that W = X ∩ W and X–W = X ∩ W’. Since y∞ = supn∈N yn is in W, yn is in W for n large enough, and similarly zn is in W’ for n large enough. Then ↟yn is included in W, so X ∩ ↟yn is included in X ∩ W = W, and X ∩ ↟zn is included in X ∩ W’ = X–W. This shows that W ∈ F ⊆ L♭(F) separates X ∩ ↟yn from X ∩ ↟zn. But we had made sure that X ∩ ↟yn is not L♭(F)-separated from X ∩ ↟zn. Hence we reach a contradiction, and the theorem is proved. ☐
Quasi-analytic spaces
An analytic space is a Hausdorff space that arises as the image of a Polish space under a continuous map. Let us drop Hausdorffness completely, and let us define a quasi-analytic space as any space that arises as the image of a continuous map f : Y → Z from a quasi-Polish space Y to an arbitrary topological space Z. (No, I am not even requiring Z to be T0.)
Clearly, every analytic space is quasi-analytic, and every quasi-Polish space is quasi-analytic.
The following is exactly the same as Theorem G, except that X is now assumed to be quasi-analytic and not quasi-Polish. I will give the proof, but you may skip it if you are satisfied with the idea that we are just going to transport Theorem G from a quasi-Polish space to its image by a continuous map.
Theorem H. Let X be a quasi-analytic space, and F be a countable family of Borel subsets of X. The following are equivalent for all Borel subsets A and B of X:
- A is L♭(F)-separated from B;
- A is L#(F)-separated from B;
- The upward closure ↑F A of A with respect to ≤F is disjoint from B.
Proof. As in the proof of Theorem G, 1 implies 2 and 2 implies 3, and the only challenge is to show that 3 implies 1.
Let X be the image of a continuous map f : Y → Z, where Y is quasi- Polish, and with the subspace topology from Z. Let G be the family of subsets f−1(B), B ∈ F. We note the following.
- The Borel subsets of X are exactly the sets of the form E’ ∩ X, where E’ is Borel in Z. In order to show this, we first remark that the collection Σ of sets of the form E′ ∩ X, where E’ is Borel in Z, forms a σ-algebra on X. Then, every open subset of X is of this form (with E’ open, even), so Σ contains OX, hence also the smallest σ-algebra that contains OX, which is the Borel σ-algebra on X. Conversely, for every open subset W of Z, W ∩ X is open hence Borel in X, and the subsets W of Z such that W ∩ X is Borel in X is clearly a σ-algebra on Z, which contains OZ, hence all the Borel subsets of Z.
- For every Borel subset E of X, f−1(E) is Borel in Y. Indeed, we write E as E’ ∩ X, where E’ is Borel in Z, and then f−1(E) = f−1(E’) is Borel in X, since inverse images of Borel sets by continuous maps are Borel.
It follows that G is a family of Borel subsets of Y, and since F is countable, so is G. Using arguments similar to the above, we have the following.
- (A) Every set in L♭(G) is of the form f−1(E) for some E ∈ L♭(F). Indeed, let E be the collection of sets of the form f−1(E), where E ∈ L♭(F). E is a σ-lattice that contains G, hence it contains L♭(G). One could also show that E is in fact equal to L♭(G), but we will not need that.
As far as specialization preorderings are concerned, we have the following.
- (B) For all y, y’ ∈ Y, y ≤G y’ implies f(y) ≤F f(y’). Indeed, if y ≤G y’ then y’ belongs to every set in G that contains y. For every E ∈ F such that f(y) ∈ E, y is in f−1(E), which is in G by definition, so y’ is in f−1(E) as well, showing that f(y’) is in E. (The implication y ≤G y’ ⇒ f(y) ≤F f(y’) is really an equivalence, but we won’t need that.)
Now let us assume that A and B are Borel subsets of X such that ↑F A is disjoint from B. Then f−1(A) and f−1(B) are Borel subsets of Y, and ↑G f−1(A) is disjoint from f−1(B): otherwise there would be a point y in f−1(A) and an element z in f−1(B) such that y ≤G z; then f(y) would be in A, f(z) would be in B, and we would have f(y) ≤F f(z) by (B), which is impossible since ↑F A is disjoint from B.
By the 3 ⇒ 1 implication of Theorem G, f−1(A) must be L♭(G)-separated from f−1(B). Using (A), there is a set E ∈ L♭(F) such that f−1(E) separates f−1(A) from f−1(B); namely, f−1(A) ⊆ f−1(E) and f−1(E) ∩ f−1(B) = ∅. For every x ∈ A, x is in X so x = f(y) for some y ∈ Y. Then y is in f−1(A), hence in f−1(E), so that x = f(y) is in E. It follows that A is included in E. Similarly, E is disjoint from B. Therefore E separates A from B. ☐
The (positive) unique structure theorem
At last we get to the promised positive unique structure theorem [1, Theorem 6.5]. It was stated there for analytic spaces, but it works just as well for quasi-analytic spaces.
Corollary (positive unique structure theorem). Let X be a quasi-analytic space.
- For every countable family F of Borel subsets of X, L♭(F)=L#(F).
- Given any two countable families F1 and F2 of Borel subsets of X, L♭(F1)=L♭(F2) if and only if F1 and F2 have the same specialization preordering (≤F1 = ≤F2).
Proof. 1. Consider any Borel subset A of X, and let B be its complement. For any family E of subsets, A is E-separated from B if and only if A belongs to E. Hence A is in L♭(F) if and only if A is L♭(F)-separated from B, if and only if A is L#(F)-separated from B (by Theorem H), if and only if A is in L#(F). But L♭(F) and L#(F) both consist of Borel sets only, so we have just shown L♭(F)=L#(F).
2. If ≤F1 = ≤F2, then L#(F1)=L#(F2), because they are both the collection of upwards-closed Borel sets with respect to the same preordering. By 1, L♭(F1)=L#(F1) and L♭(F2)=L#(F2), so L♭(F1)=L♭(F2). Conversely, if L♭(F1)=L♭(F2), then L♭(F1) and L♭(F2) have the same specialization preordering, which happens to be ≤F1 for L♭(F1) and ≤F2 for L♭(F2). ☐
The classical unique structure theorem follows immediately. We obtain it in the rather unusual situation of quasi-analytic spaces, which need not be Hausdorff or even T0. But some T0-ness is hidden in the definition of “separating points”: a family F of subsets of X separates points if and only if for any two distinct points x and y of X, some element E of F contains x and not y, or contains y and not x; equivalently, the specialization preordering of F is antisymmetric.
Corollary (unique structure theorem). Let X be a quasi-analytic space.
- Any two countable families F1 and F2 of Borel subsets of X that separate points generate the same σ-algebra.
- If X is not just quasi-analytic, but also second-countable and T0, then any countable base of the topology separates points, and any countable family of Borel subsets of X that separates points generates the whole σ-algebra of X.
Proof. We first make two remarks:
- (A) Given a countable family F of Borel subsets of X, let F be the collection of all sets from F and their complements. We claim that the σ-algebra L generated by F is exactly L♭(F).
Indeed, every element of F is clearly in L, and since L is a σ-algebra hence a σ-lattice, and since L♭(F) is the smallest σ-lattice containing F , L♭(F) is included in L.
In order to show the reverse inclusion, let E be the family of sets A such that both A and its complement are in L♭(F). It is easy to see that E is closed under countable unions and under complements, hence is a σ-algebra. Every element A of F is such that both A and its complement are in F hence in L♭(F), so F ⊆ E. Therefore, as L is the smallest σ-algebra containing F, L ⊆ E. By definition, E ⊆ L♭(F), so L ⊆ L♭(F). - (B) If F separates points, then the specialization preordering of F is equality.
Indeed, x ≤F y if and only if for every element E of F, x ∈ E implies y ∈ E, and for every complement X–E of an element E of F, x ∈ X–E implies y ∈ X–E; or equivalently, x ≤F y and y ≤F x, namely x=y since ≤F is antisymmetric, by our assumption that F separates points.
- Given two countable families F1 and F2 of Borel subsets of X that separate points, ≤F1 and ≤F2 are both identical to the equality relation by (B). By the positive unique structure theorem, L♭(F1)=L♭(F2), and by (A) this means that F1 and F2 generate the same σ-algebra.
- If X is T0, then any base of the topology separates points, in particular any countable base; naturally, such countable bases only exist if X is second-countable: this is the very definition of second countability. Given any countable family F1 of Borel subsets of X that separates points, we now apply 1 to this family and any countable base F2 of X. ☐
The (positive) unique structure theorem is pretty fascinating, in my opinion. The authors of [1] use the positive unique structure theorem to show a Hennessy-Milner type theorem for labelled Markov processes (LMP): an LMP on an analytic space simulates another one if and only if all the formulae satisfied by the first one, in a very simply logic, are also satisfied by the second one. I am pretty sure the positive unique structure theorem should have plenty of other uses as well.
- Florence Clerc, Nathanaël Fijalkow, Bartek Klin, and Prakash Panangaden. Expressiveness of probabilistic modal logics: A gradual approach. Information and Computation, 267, 145–163.
- Matthew de Brecht. Quasi-Polish spaces. Annals of Pure and Applied Logic, Volume 164, Issue 3, March 2013, pages 356-381.
- Matthew de Brecht, Jean Goubault-Larrecq, Xiaodong Jia, Zhenchao Lyu. Domain-complete and LCS-complete spaces. Proceedings of the 8th ISDT, Electronic Notes in Theoretical Computer Science 345:3–35, 2019.

— Jean Goubault-Larrecq (December 21st, 2023)
Appendix A: Scott-open subsets of continuous dcpos
Let U be any Scott-open subset of a continuous dcpo Y. Every directed family (xi)i ∈ I of elements of U has a supremum x in Y, which happens to be in U because U is upwards-closed. It is then easy to see that x is the supremum of (xi)i ∈ I in U. Hence U is a dcpo, where directed suprema are computed as in Y.
Let ≪ be the way-below relation on Y, and ≪U be the way-below relation on U; namely, x ≪U y if and only if every directed family D in U whose supremum is above y already contains an element above x. We claim that ≪U coincides with the restriction of ≪ to U.
- If x ≪U y (in particular, x, y ∈ U), then for every directed family D in Y whose supremum z=sup D is above y, we must verify that some element of D is above x in order to show that x ≪ y. Since y≤z and y is in U, which is upwards-closed, z is in U. Now z=sup D and U is Scott-open, so there is an element in D that is also in U. Using the fact that U is upwards-closed, it is then easy to see that D ∩ U is directed, and also has z as supremum. But now that supremum is a directed supremum in U, since directed suprema in U are computed as in Y. We use the fact that x ≪U y and we obtain that some element of D ∩ U is above x, as desired.
- If x ≪ y with x, y ∈ U, then for every directed family D in U whose supremum z=sup D (in U) is above y, there is an element of D above x; this is because directed suprema in U are computed as in Y. Therefore x ≪U y.
Given any basis B of the continuous dcpo Y, it follows that B ∩ U is a basis of the dcpo U, and therefore that U is itself a continuous dcpo, and even an ω-continuous dcpo if B can be taken to be countable. Indeed, every element y of U, seen as an element of Y, is the supremum of some directed family D of elements x of B such that x ≪ y. Since U is Scott-open, and as above, D ∩ U is a directed family too, and its supremum is also equal to y. Additional, each element x of D ∩ U is in B ∩ U, and we have x ≪U y because ≪U coincides with the restriction of ≪ to U, as we have argued above.
We conclude this by showing that the subspace topology on U is the Scott topology. Every open subset of U in the subspace topology is of the form V ∩ U where V is Scott-open in Y; but V ∩ U is itself Scott-open in Y, and from this it is easy to see that it is Scott-open in X, since directed suprema are computed in U as in Y. Conversely, the Scott topology on U has a basis of sets ↟U x, with x in B ∩ U (Theorem 5.1.17 in the book); let me write ↟U x for {y ∈ U | x ≪U y}, and ↟x for {y ∈ Y | x ≪ y}. Since ≪U coincides with the restriction of ≪ to U, and since U is upwards-closed, ↟U x is equal to ↟x, and each one is open in Y.
Appendix B: Scott-closed subsets of dcpos
Let C be any Scott-closed subset of a continuous dcpo Y. Every directed family (xi)i ∈ I of elements of C has a supremum x in Y, which happens to be in C because C is closed under directed suprema. It is then easy to see that x is the supremum of (xi)i ∈ I in C. Hence C is a dcpo, where directed suprema are computed as in Y.
Let ≪ be the way-below relation on Y, and ≪C be the way-below relation on C; namely, x ≪C y if and only if every directed family D in C whose supremum is above y already contains an element above x. We claim that for all x, y ∈ C, x ≪ y implies x ≪C y.
Indeed, for every directed family D in C whose supremum z=sup D (in C) is above y, there is an element of D above x; this is because directed suprema in C are computed as in Y. Therefore x ≪C y. We don’t know yet the converse, namely that x ≪C y implies x ≪ y, but we will prove it shortly.
Before we do so, we observe that C is a continuous dcpo. In fact, given any basis B of the continuous dcpo Y, we claim that B ∩ C is a basis of C; this will show that C is even ω-continuous if Y is. For every element y of C, y is the supremum of a directed family of elements xi, i ∈ I, with xi ≪ y and xi ∈ B. This is because Y is a continuous dcpo. Since C is downwards-closed, each of those elements xi is in C, and we have just seen that xi ≪ y implies xi ≪C y, and the claim is proved.
We now have enough to show that ≪C coincides with the restriction of ≪ to C. It remains to show that for all x, y in C such that x ≪C y, we have x ≪ y. Since Y is continuous, y is the supremum of a directed family of elements xi, i ∈ I, with xi ≪ y. Each xi is in C since C is downwards-closed, so y is also the supremum of the elements xi, taken in C. We use x ≪C y to obtain the existence of an element xi such that x ≤ xi. Combined with xi ≪ y, it follows that x ≪ y.
We conclude this by showing that the subspace topology on C is the Scott topology. The open subsets of C are the unions of sets of the form ↟C x, where x ranges over some subset of C; let me write ↟C x for {y ∈ C | x ≪C y}, and ↟x for {y ∈ Y | x ≪ y}. We have just seen that ≪C coincides with the restriction of ≪ to C, so ↟C x = ↟x ∩ C. Hence the Scott-open subsets of C are exactly the intersection of Scott-open subsets of Y with C, namely the open subsets in the subspace topology.
