I recently came across this funny fact: given a coherent, well-filtered space X, one can give an explicit description of the compact closed sets in Xpatch, the space obtained by equipping X with its patch topology—and we do not need local compactness. (I will explain more below.) The story is that I was looking for a certain result in a paper by K. Keimel and J. Lawson [1]; I could not find it, so I proved it; then I found it as item 5 of Lemma 7.1 of [1]; its proof is based on item 4 of the same lemma, and I then discovered that this very item 4 was faulty; then Jimmie Lawson sent me a corrected proof, which was much simpler than the one I originally had. This is the proof that I will give below.
The patch space
Given any topological space X, one can build the patch space Xpatch of X as containing the same points as X, but with the coarsest topology that contains the original topology of X, plus all the complements of compact saturated subsets. In other words, the open subsets of Xpatch (for short, the patch-open sets) are the unions of basic patch-open sets U–Q, where U ranges over the open subsets of X and Q ranges over the compact saturated subsets of X.
In Section 9.1 of the book, you will see that there is a wonderful theory around this when X is stably compact, namely locally compact, coherent, compact, and sober. In that case, Xpatch is a compact Hausdorff space.
We are going to drop compactness and local compactness. Most of the theory above then falls apart, as the following example shows, but some can be salvaged provided that X is coherent and well-filtered.
Example 1. We consider the complete lattice Lfan, already studied in the posts of May 20th and June 20th 2024. We have seen that it is sober and coherent in its Scott topology, but not locally compact (even not core-compact). I will not reproduce the formal definition, but here it is in pictures.
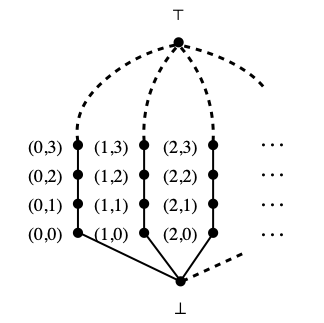
For every function f : N → N, let Uf be the collection of points (m, n) with n≥f(m), plus ⊤. The (Scott-)open subsets of Lfan are the sets Uf, where f ranges over the functions from N to N, plus the empty set, plus the whole space Lfan. The compact saturated subsets are the finitary compact subsets, namely the upward closures of finite subsets. We have seen all that in the aforementioned posts. It follows that any non-empty basic patch-open set U–Q contains cofinitely many infinite columns; I am calling “infinite column” any set of the form {(m, n), (m, n+1), (m, n+2), …} (without top), for some natural number m, and “cofinitely many” means “for every value of m except for finitely many”.
As a consequence, any two non-empty patch-open subsets intersect; in fact, their intersection also contains cofinitely many infinite columns. This implies that Lfanpatch is not sober; a rather unexpected fact, considering that Lfan is sober. In particular, Lfanpatch is not Hausdorff; if you don’t remember that every Hausdorff space is sober (Proposition 8.2.12 in the book), realize that any two open neighborhoods of two points must meet on cofinitely many infinite columns, hence will never be disjoint.
Still, the patch space enjoys a few properties, even when X is not locally compact.
Lemma A. For every T0 space X, Xpatch is T1.
Proof. Let x and y be two distinct points of X. We need to find an open neighborhood of each that does not contain the other. Since X is T0, one of the two points is not below the other, say x≰y. In particular, there is an open neighborhood U of x in X (hence in Xpatch) that does not contain y. Also, the complement of the compact saturated set ↑x is open in Xpatch, contains y, and does not contain x. ☐
The if direction of the following is Lemma VI-6.5 of [2]. This entails that Lfanpatch is compact.
Lemma B. Let X be a coherent well-filtered space. Xpatch is compact if and only if X is.
Proof. If Xpatch is compact, then every open cover of X (by open subsets of X) is also an open cover of X by open subsets of Xpatch; we can therefore extract a finite subcover, showing that X is compact.
Conversely, we assume that X is coherent, compact, and well-filtered. In a coherent space, every non-empty finite intersection of compact saturated sets is compact saturated (that is basically the definition of coherence); this extends to all finite intersections of compact saturated sets when X is compact, since the only additional case, that of the intersection of an empty family, is X itself.
We use Alexander’s subbase lemma (Theorem 4.4.29 in the book). Let Xpatch be covered by a family of subbasic patch-open sets: open subsets Ui of X, where i ranges over some index set I, and complements X–Qj of compact saturated subsets Qj of X, where j ranges over some index set J. Equivalently, ∩j ∈ J Qj ⊆ ∪i ∈ I Ui.
The intersection ∩j ∈ J Qj can be rewritten as a filtered intersection of finite intersections QA ≝ ∩j ∈ A Qj (where A ranges over the finite subsets of J). Because X is coherent and compact, each QA is compact saturated. In a well-filtered space, any filtered family of compact saturated sets whose intersection is included in a given open set contains an element already included in that open set (that is the definition of well-filteredness); hence QA ⊆ ∪i ∈ I Ui for some finite subset A of J. Since QA is compact, there is a finite subset B of I such that QA ⊆ ∪i ∈ B Ui. Therefore the finitely many sets Ui with i ∈ B and Qj with j ∈ A form a finite subcover of Xpatch. ☐
Hence, in one direction, we do not need X to be locally compact in order for Xpatch to be compact. But, and assuming X to be coherent and well-filtered, we need it to be compact. Here are a few examples where Xpatch is not compact.
Example 2. The simplest example is N with its discrete topology. Then Npatch is also N with the discrete topology (the patch space of any Hausdorff space is itself, because any compact subset is already closed), but Npatch=N is not compact.
Example 3. For another, more pathological example, let us consider the space X obtained from Lfan by removing its bottom element. Its (Scott-)open subsets are exactly the open subsets of Lfan that are included in Lfan (namely the empty set, plus all the sets Uf), and then X is an open subspace of Lfan. The closed subsets of X are then exactly the intersections of the closed subsets of Lfan with X, namely the non-empty closed subsets of Lfan minus the bottom element. It follows easily from the fact that Lfan is sober that X is sober.
Because X is a topological subspace of Lfan, the compact saturated subsets of X are those of Lfan that are included in X; hence X, too, is coherent.
Also, the compact saturated of X are its finitary compact subsets. Then X is not compact, because it is not finitary compact. As a consequence of Lemma B, Xpatch is not compact. Finally, and for the same reasons as with Lfanpatch, Xpatch is not sober, hence not Hausdorff.
The K-patch topology
In the sequel, we will take a slightly more abstract view, and we will replace compact saturated subsets by sets from a fixed, given family K of subsets of X. We will require the following assumptions in most of our results to come:
- every non-empty finite intersection of members of K (in particular every member of K) is compact in X;
- K has the non-empty finite intersection property with respect to open subsets, namely: for every non-empty family (Ki)i ∈ I of elements of K, for every open subset U of X, if ∩i ∈ I Ki ⊆ U then ∩i ∈ A Ki ⊆ U for some non-empty finite subset A of I already.
The non-empty finite intersection property in assumption 2 is an abstraction of coherence and well-filteredness, and is equivalent to it when K is the collection of compact saturated subsets of X. Taking this abstract view isolates the assumptions we will need precisely.
You may be more familiar with the finite intersection property, which would state: for every (possibly empty) family (Ki)i ∈ I of elements of K, for every open subset U of X, if ∩i ∈ I Ki ⊆ U then ∩i ∈ A Ki ⊆ U for some (possibly empty) finite subset A of I already. This is equivalent to property 2, but property 2 will be what we need. (Property 2 implies the finite intersection property: if the family (Ki)i ∈ I is empty and ∩i ∈ I Ki ⊆ U, then take A to be empty. Conversely, if K has the finite intersection property, then for every non-empty family (Ki)i ∈ I of elements of K such that ∩i ∈ I Ki ⊆ U, there is a finite subset A of I such that ∩i ∈ A Ki ⊆ U. Add any element of I to A to make sure that A is non-empty—that is possible since I is non-empty—and then you get property 2.)
Abstracting away from compact saturated sets and considering families K satisfying assumptions 1 and 2 may serve in other circumstances. For example, one may think of considering the collection of finitary compact subsets of X for K, that is, the collection of upward closures of finitely many points. In this setting, assumption 2 is what Lawson and Xu call property R in [Definition 30, 3]; their statement of property R is obtained by removing the two occurrences of “non-empty” in assumption 2, but we have just argued that this is equivalent. Still in this setting, assumption 1 is equivalent to the fact that every intersection ↑x1 ∩ … ∩ ↑xn with n≥1 is compact, and this is a property that Lawson and Xu consider in [Proposition 40, 3], except with n=0 as well, which implies that X is compact (an assumption we do not make). I may talk about some of the results of [3] another day.
We define the K-patch topology on X as the coarsest topology containing the original topology and the complements of members of K. If K is closed under finite unions, a base of the K-patch topology on X is given by sets of the form U–K where U is open in X and K ∈ K; in general, a base is given by sets of the form U–(K1 ∪ … ∪ Kn) where U is open in X, n ∈ N, and K1, …, Kn are members of K.
If K is the collection of all compact saturated subsets of X, then the K-patch topology is the patch topology. If K is the collection of finitary compact subsets of X, where X is a poset in its Scott topology, then the K-patch topology is the Lawson topology of X. The latter generalizes to any topological space X, still taking K to be the collection of finitary compact subsets, and is the topology called O(X) ⋁ ω(X) in [Section 3, 3].
Lemma B generalizes naturally to our new setting.
Lemma C. Under assumptions 1—2, X is compact in the K-patch topology if and only if it is compact in its original topology.
Proof. The proof is essentially the same. We deal with the if direction by relying on Alexander’s subbase lemma, too. Let X be covered by a family of subbasic K-patch-open sets: open subsets Ui of X, where i ranges over some index set I, and complements X–Kj of elements Kj of K, where j ranges over some index set J. Equivalently, ∩j ∈ J Kj ⊆ ∪i ∈ I Ui.
If J is empty, then X ⊆ ∪i ∈ I Ui, and since we have assumed X compact, X is included in UB ≝ ∪i ∈ B Ui for some finite subset B of I, yielding the desired open cover.
If J is non-empty, then by assumption 2 there is a non-empty finite subset A of I such that KA ≝ ∩j ∈ A Kj is included in ∪i ∈ I Ui. By assumption 1, KA is compact. Therefore there is a finite subset B of I such that KA ⊆ ∪i ∈ B Ui. The desired open cover consists of the sets Ui with i ∈ B and the sets X–Kj with j ∈ A. ☐
The K-lens topology
A very nice idea of [1] is to consider yet another topology, which they call the lens topology; this is the smallest topology on X that makes every lens closed, where a lens is a non-empty intersection of a compact saturated set with a closed set. (Non-emptiness is irrelevant here, by the way, since we will be taking finite unions of such sets, including the empty union.)
Hence, given a family K of subsets of X as above, let us call a K-lens any intersection K ∩ C of an element K of K with a closed subset C of X. (I will allow for empty intersections, too.) Let KL be the collection of finite unions of K-lenses, and let us call K-lenticularly closed any non-empty intersection of elements of KL.
The K-lenticularly closed subsets of X are closed under arbitrary non-empty intersections, and also under finite unions (just distribute the finite unions over non-empty intersections). Hence they almost form the family of closed subsets of a topology. Only the empty intersection—the whole space—may be missing.
Let us call the K-lens topology the topology on X whose closed subsets are the K-lenticularly closed subsets of X, plus X itself. Now that is a topology, even if K satisfies none of our assumptions 1–2. Following [1], we will call the lens topology the K-lens topology when K is the collection of all compact saturated sets. We have the following properties.
Fact D. The K-lens topology is the coarsest that makes every K-lens closed.
Fact E. The K-lens topology is coarser than the K-patch topology.
Fact E is clear. It suffices to observe that every K-lens K ∩ C is closed in the K-patch topology, and indeed K ∩ C is the intersection of a member of K, which by definition if closed in the K-patch topology, and with C, which is also closed in K-patch topology. What is probably more mysterious is what difference there may be between the two topologies. Intuitively, in the K-lens topology, each time you pick a closed set C (in X), you need to intersect it with some member K of K before you get a closed subset in the K-lens topology; but C itself is already closed in the K-patch topology. Here is an example that illustrates how far apart the two topologies can be.
Example 4. Let X be R with the Scott topology of its usual ordering ≤. Its open subsets are the empty set, R itself, and the half-open intervals ]a, ∞[. Its compact saturated subsets are the empty set and the half-closed intervals [a, ∞[. We let K be the collection of those compact saturated subsets.
- The (K-)patch topology is the usual metric topology on R, with a base of open subsets of the form ]a, b[; with that topology, R is Hausdorff and locally compact.
- In comparison, let us look at the (K-)lens topology. The non-empty (K-)lenses are the closed bounded intervals [a, b]. Hence KL consists of all finite unions of closed bounded intervals, and those sets are all closed and bounded. It follows that all the K-lenticularly closed subsets are also closed and bounded.
Conversely, let us consider any closed and bounded subset A of R. Its complement is open, hence equal to a union of open intervals ]ai, bi[, i ∈ I. If a is a lower bound of A and b is an upper bound of A, then A = [a, b] ∩ ∩i ∈ I (R – ]ai, bi[): if I is empty, this is equal to [a, b], which is a lens, otherwise A = ∩i ∈ I ([a, b] – ]ai, bi[) (yes, this equality only holds if I is non-empty); but each set [a, b] – ]ai, bi[ is a union of at most two closed intervals ([a, ai] and [bi, b]; maybe only one if b<bi or ai<a, maybe zero) hence is in KL, so that A is K-lenticularly closed.
We have obtained a complete characterization of the K-lenticulary closed subsets of R (with its Scott topology): they are the closed bounded subsets of R (with its usual metric topology). You may remember that they are exactly the compact subsets of R with its usual metric topology, and that is no accident, as we will discover below. - The closed subsets in the (K-)lens topology are therefore the closed bounded subsets of R (with its usual metric topology), plus R itself. Hence it misses a lot of the patch-closed subsets of X, namely of the closed—not necessarily bounded—subsets of R (with its metric topology). For example, [0, ∞[ and ]∞, 0] are closed in the (K-)patch topology but not in the (K-)lens topology.
- Worse, the (K-)lens-topology is not even sober! Indeed, R itself is irreducible closed in that topology: if R is included in the union of two closed subsets C and C’ of the (K-)lens topology, well, they cannot be both bounded, otherwise their union would be bounded, too; so C or C’ must be equal to the whole of R. Non-sobriety follows from the fact that R is not the closure of one point, because the (K-)lens topology is T1; this can be checked by hand, or using the following lemma.
We will see in Proposition M when exactly the lens and patch topologies coincide.
Lemma F. For every T0 space X, if K contains all sets ↑x as members, then the K-lens topology is T1. In particular, the lens topology is T1 on every coherent, well-filtered, T0 space.
Proof. The proof is as with Lemma A. Let x and y be two distinct points of X. Since X is T0, one of them is not below the other, say x≰y. In particular, there is an open neighborhood U of x in X that does not contain y. That may not be open in the K-lens topology, but U ∪ (X–↑y), which is the complement of the K-lens (X–U) ∩ ↑y, is, and contains x and not y.
In order to find an open neighborhood of y that does not contain x (in the K-lens topology), we consider ↑x: that is in K, hence also in KL, because it is the K-lens ↑x ∩ X. The complement of ↑x is then open in the K-lens topology, contains y, and does not contain x. ☐
The K-lenticularly closed subsets are compact and closed in the K-patch topology
We will see that the K-lenticularly closed subsets of X are all compact in the K-patch topology, provided that K satisfies assumptions 1–2. As I said earlier, the proof was given to me by Jimmie Lawson, and replaced a more complicated proof of mine.
Lemma G. Let K satisfy assumptions 1–2. Then X with the K-lens topology is compact.
Proof. We use Alexander’s subbase lemma, just like in the proofs of Lemma B and Lemma C. Let us consider an open cover of X by subbasic open sets of the K-lens topology, namely by complements of lenses Li ≝ Ki ∩ Ci, where i ranges over some index set I; each Ki is in K, and each Ci is closed in X. If I is empty, then X itself is empty, and then certainly compact in whatever topology we may think of. Therefore we will assume that I is non-empty.
Taking complements, we have ∩i ∈ I (Ki ∩ Ci) = ∅, equivalently ∩i ∈ I Ki ∩ ∩i ∈ I Ci = ∅. Let Ui be the complement of Ci. We can rewrite the latter as ∩i ∈ I Ki ⊆ ∪i ∈ I Ui. By assumption 2, ∩i ∈ A Ki ⊆ ∪i ∈ I Ui for some non-empty finite subset A of I. By assumption 1, ∩i ∈ A Ki is compact, so there is a finite subset B of I such that ∩i ∈ A Ki ⊆ ∪i ∈ B Ui. Then ∩i ∈ A ∪ B Ki ⊆ ∪i ∈ A ∪ B Ui, and this entails that ∩i ∈ A ∪ B Li is empty, hence that the complements of the lenses Li with i ranging over A ∪ B form a finite subcover of X. ☐
The important trick is the following lemma.
Lemma H. Let K be arbitrary. For every K-lenticularly closed subset F of X, the subspace topologies on F induced by the inclusion into X with either its K-patch or K-lens topology are the same.
Proof. By Fact E, the K-lens topology is coarser than the K-patch topology, so the induced topologies on F obey the same inclusion relation. Conversely, we need to show that every closed subset of F in the topology induced by the inclusion into X with its K-patch topology, namely every set of the form D ∩ F where D is patch-closed in X, can be written as an intersection D’ ∩ F where D’ is closed in the K-lens topology on X.
- We show this first when D is closed in X. We write F as ∩i ∈ I ∪j=1ni Lij, where I is non-empty and each Lij is a K-lens Kij ∩ Cij (Kij a member of K, Cij a closed subset of X). Then D ∩ F = ∩i ∈ I ∪j=1ni (D ∩ Lij) (an equality that only holds because I is not empty!), and each D ∩ Lij is equal to Kij ∩ (D ∩ Cij), which is a K-lens. Therefore D’ ≝ D ∩ F is K-lenticularly closed, hence closed in the K-lens topology, and D ∩ F = D’ ∩ F.
- Next, we show the same statement when D is in K. We write F just like in the previous case. Then each D ∩ Lij is equal to the intersection of the two K-lenses D ∩ Cij and Kij (= Kij ∩ X, with X being the closed part), hence is closed in the K-lens topology on X. It follows that D’ ≝ D ∩ F = ∩i ∈ I ∪j=1ni (D ∩ Lij) is also closed in the K-lens topology on X, and, as in the previous item, D ∩ F = D‘ ∩ F.
- In general, D is a union ∩k ∈ K ∪l=1mk Dkl of finite intersections of sets Dkl that are closed in X or members of K. If K is empty, then D=X, which is closed in X, so the case is covered by the first item above. Otherwise, by the previous two items, the sets D’kl ≝ Dkl ∩ F are closed in the K-lens topology, so D’ ≝ ∩k ∈ K ∪l=1mk D’kl is, too, and D ∩ F = ∩k ∈ K ∪l=1mk (Dkl ∩ F) = ∩k ∈ K ∪l=1mk (D’kl ∩ F) = D‘ ∩ F. (The first and last equality depend on K being non-empty.) ☐
Lemma H allows us to obtain the following, otherwise pretty difficult result.
Lemma I. Let K satisfy assumptions 1–2. Then every K-lenticularly closed subset of X is compact in the K-patch topology.
Proof. Let F be a K-lenticularly closed subset of X. Then F is closed in the K-lens topology. But, with the K-lens topology, X is compact by Lemma G. Every closed subset of a compact space is compact, so F is compact in the K-lens topology. We now look F as a subspace, namely we equip it with the topology induced by the inclusion in X with its K-lens topology. With that topology, F becomes a compact space.
By Lemma H, that topology is also the topology induced by the inclusion in X with its K-patch topology. Hence F is also a compact space in that topology. Explicitly, this means that for every cover of F by a family of sets Oi ∩ F, where i ranges over some index set I and each Oi is open in the K-patch topology on X, F is included in a finite union of those sets. Equivalently, reverting back to the view of F as a subset of X, every cover of F by a family of K-patch-open subsets Oi of X has a finite subcover. Therefore F is compact in the K-patch topology. (To spell it more briefly: compact subspaces are the same thing as compact subsets, with the subspace topology.) ☐
Every K-lenticularly closed subset of X is also closed in the K-patch topology, because they are all closed in the coarser K-lens topology (see Fact E). Hence:
Corollary J. Let K satisfy assumptions 1–2. Then every K-lenticularly closed subset of X is compact and closed in the K-patch topology.
The compact closed subsets in the patch topology of a coherent well-filtered space
If X is a coherent well-filtered space, then its collection of compact saturated subsets satisfies assumptions 1 and 2. We agree to drop the “K-” prefix in this case. By Corollary J, every lenticularly closed subset, namely every non-empty intersection of finite unions of lenses, is compact and closed in Xpatch. We can say more.
Theorem K. Let X be a coherent well-filtered space. The compact closed subsets of Xpatch are exactly the lenticularly closed subsets of X.
Proof. It remains to show that every compact closed subset F of Xpatch is lenticularly closed. Since F is patch-closed, its complement is a union of finite intersections of open and complements of compact saturated subsets of X. But finite intersections of open sets are open, finite unions of compact saturated subsets are compact saturated, so one can simplify that and simply say that we can write the complement of F as a union ∪i ∈ I (Ui ∩ (X–Qi)), where I is some index set, each Ui is open in X, and each Qi is compact saturated in X. Let Ci be the complement of Ui, then F = ∩i ∈ I (Ci ∪ Qi).
Since the patch topology is finer than the original topology on X, every patch-compact subset of X is compact in the original topology: every cover by open subsets of X is in particular a cover by patch-open subsets. It follows that F is compact in X, and therefore that its upward closure Q≝↑F is compact saturated in X.
Plainly, F = Q ∩ F, and therefore we can write F as Q ∩ (∩i ∈ I (Ci ∪ Qi)), and then as the intersection of Q and of the sets (Q ∩ Ci) ∪ (Q ∩ Qi). Every compact saturated subset of X is a lens; e.g., Q is the intersection of Q with the closed set X (and remember we are not insisting that lenses be non-empty in this post). Similarly, Q ∩ Qi is compact saturated, since X is coherent, hence a lens; and Q ∩ Ci is a lens by definition. It follows that F is a non-empty finite intersection of the finite unions of lenses Q and (Q ∩ Ci) ∪ (Q ∩ Qi), i ∈ I, and therefore that F is lenticularly closed. ☐
Remark L. The last part of the proof shows that the compact closed subsets of Xpatch can even be written as non-empty intersections of unions of at most 2 lenses each.
The proof of Theorem K does not generalize to give a characterization of the compact closed subsets in the K-patch topology for arbitrary families K satisfying assumptions 1 and 2. The best I can say (without spending too much effort on it) is that the K-lenticularly closed subsets of X are exactly the compact closed subsets of X in its K-patch topology that are included in some finite union of members of K. I don’t find this particularly remarkable, hence I will not bother making it a theorem standing on its own.
The proof is the same. In one direction, every K-lenticularly closed subset is compact and closed in the K-patch topology by Corollary J, and, being a non-empty intersection of members of KL, it must be included in one of them. Now every member of KL is a finite union ∪i=1n (Qi ∩ Ci) of K-lenses, which is included in the finite union ∪i=1n Qi of members of K.
In the other direction, let F be a compact closed set in the K-patch topology that is included in a finite union Q ≝ ∪i=1n Qi of members of K. We note that Q is in KL. We write F as Q ∩ (∩i ∈ I (Ci ∪ Qi)) as in the proof of Theorem K, namely as the intersection of the non-empty family consisting of Q (in KL) and of the sets (Q ∩ Ci) ∪ (Q ∩ Qi). Each set Q ∩ Ci is itself in KL, and each set Q ∩ Qi, while not necessarily in KL, is K-lenticularly closed, being the intersection of two K-lenses; therefore (Q ∩ Ci) ∪ (Q ∩ Qi) is also K-lenticulary closed, and hence F is, too.
Characterizing when the lens and patch topologies coincide
I could have concluded with Theorem K. I guess that is a beautiful enough result. However, I feel I have to mention that one can say a bit more. After Example 4, notably, I had said we would see later when the lens and patch topologies coincide. Here we are.
Proposition M. Given any coherent well-filtered space X, the lens and patch topologies coincide if and only if Xpatch is compact, if and only if X is compact in its original topology.
Proof. If X is compact, then it is a lens, hence it is lenticularly closed. We can then apply Lemma H to F≝X, and then the (subspace topologies induced on X by the inclusion into itself with) the lens and patch topologies coincide.
If the lens and patch topologies coincide, then X is compact in the latter, since it is compact in the former by Lemma G.
If X is compact in the patch topology, then it is compact in its original topology, see Lemma C. ☐
A form of well-filteredness for K-lenticularly closed subsets
Finally, the following variant on the notion of well-filteredness deserves to be mentioned. Let me recall that assumption 2 says that K has the non-empty finite intersection property with respect to open subsets of X, or equivalently the finite intersection property with respect to open subsets—it does not matter whether we say “non-empty” or not.
Proposition N. Let K satisfy assumptions 1–2. The collection of K-lenticularly closed subsets of X has the (non-empty) finite intersection property with respect to the open subsets of X in the K-patch topology.
In other words, for every (non-empty) family (Fi)i ∈ I of K-lenticularly closed subsets of X, for every open subset O of X in its K-patch topology, if ∩i ∈ I Fi ⊆ O then ∩i ∈ A Fi ⊆ O for some (non-empty) finite subset A of I already.
Proof. By Corollary J, each Fi is compact and closed in the K-patch topology, so Fi–O is, too. Their complements O ∪ (X–Fi) are then open in the K-patch topology. Now ∩i ∈ I Fi ⊆ O means that the sets Fi–O have empty intersection, so the sets O ∪ (X–Fi) form an open cover of X in the K-patch topology.
No, we don’t know whether X is compact in that topology, but we don’t care. The family (Fi)i ∈ I is non-empty, so we can pick one of its elements, call it Fi[0]. By Lemma I, Fi[0] is compact in the K-patch topology, and the sets O ∪ (X–Fi) with i ∈ I form an open cover of Fi[0], since they even cover the larger set X. Therefore there is a finite subset A of I such that Fi[0] is included in ∪i ∈ A (O ∪ (X–Fi)). Without loss of generality, we may assume that the index i[0] is in A; otherwise, add it to A. Then ∩i ∈ A (Fi–O) is included in Fi[0]. Now ∩i ∈ A (Fi–O) is the complement of ∪i ∈ A (O ∪ (X–Fi)), which contains Fi[0], so ∩i ∈ A (Fi–O) is included in the complement of Fi[0]. Being included in both Fi[0] and its complement, ∩i ∈ A (Fi–O) is empty. Equivalently, ∩i ∈ A Fi ⊆ O. ☐
Corollary O. Let X be a coherent, well-filtered space. The collection of compact closed subsets of Xpatch has the (non-empty) finite intersection property with respect to the open subsets of Xpatch.
In particular, if Xpatch is a KC-space (still assuming X coherent and well-filtered), namely a space in which every compact subset is closed, then Xpatch is itself well-filtered. Every Hausdorff space, for example, is a KC-space. In that situation, where X is coherent and well-filtered and Xpatch is a KC-space, Theorem K gives a complete characterization of the compact subsets of Xpatch: they are, once again, exactly the lenticularly closed subsets.
This naturally leads to many questions, among others the following.
- Given a coherent well-filtered space X whose patch space Xpatch is a KC-space, is Xpatch necessarily Hausdorff? One should first have a look at Example 1 or Example 4 and check whether the patch spaces there are KC-spaces; if so, the answer to the question would be an easy “no”.
- Can one characterize the compact subsets of Xpatch when X is coherent and well-filtered, and not just its compact closed subsets?
- Under what natural additional conditions on K, beyond assumptions 1–2, would the compact closed subsets of X in its K-patch topology be exactly its K-lenticulary closed subsets? (Looking at the discussion after Remark L, one such condition is “X is a finite union of elements of K“, or “every compact closed subset in the K-patch topology is included in a finite union of elements of K“, but let me say that I consider this pretty uninteresting.)
- Taking K to be the collection of finitary compact subsets, namely the upward closures of finite sets, the K-patch topology is a generalization of the Lawson topology: what are its compact closed subsets? This topology was studied recently by Lawson and Xu [3], as I said earlier.
- Klaus Keimel and Jimmie Lawson. Measure extension theorems for T0-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Jimmie Lawson and Xiaoquan Xu. T0-spaces and the lower topology. Mathematical Structures in Computer Science, 1–24, 2024. doi:10.1017/S0960129524000240

— Jean Goubault-Larrecq (October 20th, 2024)
