Last time, we had started to study the following poset Lfan, introduced independently in [3, 1, 4]: Lfan is N × N, with equality as ordering on the first component and the usual ordering on the second component, plus an extra bottom element ⊥, plus an extra top element ⊤:
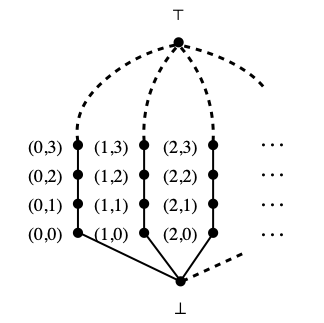
We had seen that Lfan is a complete lattice with the Chen-Kou-Lyu property—in particular, (Lfan × Lfan)σ = (Lfan)σ × (Lfan)σ, where the σ subscript means “with the Scott topology”—although it is neither core-compact nor first-countable (in its Scott topology).
The Scott topology on Lfan can be described explicitly. For every function f : N → N, let Uf be the subset of those pairs (m, n) of N × N such that n≥f(m), plus ⊤.
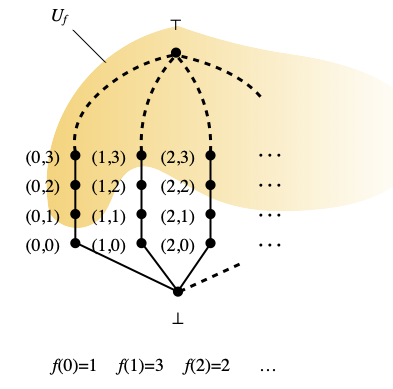
Then the Scott-open subsets of Lfan are exactly the sets Uf, where f ranges over the functions from N to N, plus the empty set, plus the whole space Lfan. Additionally, Uf ⊆ Ug if and only if f≥g, so that O(Lfan) is order-isomorphic to the poset (N → N)op of functions from N to N, ordered with the opposite ordering ≥ (not ≤), with an additional bottom element (∅) and an additional top element (Lfan).
Sobriety
We start this month’s post with a nice piece of news about Lfan.
Lemma A. Lfan is sober in its Scott topology.
Proof. Let C be an irreducible subset of Lfan. It is non-empty, and downwards-closed, hence contains ⊥. If it only contains ⊥, then C is the downward closure of ⊥. If C contains ⊤, then C = ↓⊤. Henceforth, let us assume that C is neither of those. But C is closed, the closed sets are the complements of open sets, and we know what the open sets are: C is the complement of Uf, for some function f from N to N. Also, f is not the constant 0 function, since otherwise C would be {⊥}.
For every m ∈ N, let us say that C has a non-trivial column, and precisely that it has non-trivial column number m if and only if C contains a point (m, n) for some n, equivalently if and only if f(m)≠0. If so, there is a largest point (m, n) in C’s column m, namely (m, f(m)–1). Since f is not the constant 0 function, C has at least one non-trivial column. We claim that it has exactly one.
Otherwise, let us say that columns m and m’ are non-trivial, with m≠m’. Let g : N → N be as f, except that g maps m to f(m)–1, and let g’ be as f except that it maps m’ to f(m’)–1. Then C intersects Ug at (m, f(m)–1), Ug’ at (m’, f(m’)–1), but C does not intersect Ug ∩ Ug’, since the latter is equal to Usup(g,g’) = Uf. This contradicts the fact that C is irreducible (see Trick 8.2.3 in the book).
Therefore C has exactly one non-trivial column, say with number m. Then C = ↓(m, f(m)–1). In all cases, C is the downward-closure of a (unique) point, so Lfan is sober. ☐
This was proved by Chen, Kou and Lyu [1, Example 4.13].
Weak Hausdorffness, and being a maximal limit space
The following properties were not considered by Chen, Kou and Lyu [1], or by Hertling [4], or by Xu, Shen, Xi and Zhao [3], but I think they deserve to be mentioned, specially considering that they were the topic of some of my recent posts.
A space X is weakly Hausdorff in the sense of Klaus Keimel and Jimmie Lawson [5] if and only if for any two points x and y in X, for every open neighborhood W of ↑x ∩ ↑y, there is an open neighborhood U of x and there is an open neighborhood V of y such that U ∩ V ⊆ W. I have already written a few times about that notion.
Lemma B. Lfan is weakly Hausdorff in its Scott topology.
Proof. We take two points x and y and an open neighborhood W of ↑x ∩ ↑y. The existence of U and V is obvious if x≤y (or symmetrically if y≤x): simply take the whole space for U and W for V. Hence let us assume that x and y are incomparable. Then none of x or y is equal to ⊤ or to ⊥, so we can write x as (m, n) and y as (m’, n’), where additionally m≠m’.
The intersection ↑x ∩ ↑y is then equal to {⊤}. If W is the whole space Lfan, then we can simply take U and V equal to the whole space as well. Henceforth, let us assume that W is a proper open subset of Lfan. Since W contains {⊤}, it is non-empty, hence of the form Uf, for some function f : N → N, by Lemma E. We let g : N → N be defined as f, except that it maps m to 0; and g’ be defined as f except that it maps m’ to 0. Then x = (m, n) is in Ug, y = (m’, n’) is in Ug’, and Ug ∩ Ug’ = Usup(g,g’) = Uf = W, so we can take U ≝ Ug and V ≝ Ug’. ☐
In this post (March 2024) on Hoover’s maximal limit spaces [6], namely on spaces in which every convergent filter has a unique largest limit, we have shown (Theorem I there) that a maximal limit space is the same thing as a weakly Hausdorff, binary-bounded-sup-complete, monotone convergence space. By Lemma A, Lfan is sober, hence a monotone convergence space (see Proposition 8.2.34 in the book), it is weakly Hausdorff by Lemma B, and it is certainly binary-bounded-sup-complete, since it is a complete lattice, as we have seen last time. Therefore:
Proposition C. Lfan is a maximal limit space.
In particular, it is coherent, too. We will retrieve this below, when we study the compact saturated subsets of Lfan.
The dcpo O(Lfan) of Scott-open subsets of Lfan
The complete lattice O(Lfan) of Scott-open subsets of Lfan consist of the sets Uf, with f : N → N, ordered with the opposite of the pointwise ordering on functions f, plus a top element (the whole space Lfan), plus a bottom element (the empty set).
Let us write Nω for the set of natural numbers N, with an extra element ω above all natural numbers. We order it in the usual way: 0 ≤ 1 ≤ … ≤ n ≤ … ≤ ω.
For every function g from N to Nω, let dom g be the set of numbers m ∈ N such that g(m)≠ω. This is the domain of g, which I will write as dom g. We let FF be the set of functions f from N to Nω whose domain is finite, ordered pointwise. Hertling [4, before Lemma 4.13] uses actual total functions from a finite subset of N to N (not Nω), but I think this definition of FF will be more practical.
For every g ∈ FF, let Vg be the collection of Scott-open subsets of Lfan of the form Uf with f≤g, plus Lfan itself. The following is due to Hertling [4, Lemma 4.14].
Proposition D. The sets Vg, g ∈ FF, plus {Lfan} and O(Lfan), form a base of the Scott topology on O(Lfan).
Proof. We first check that Vg is Scott-open. It is clear that Vg is upwards-closed; notably, if Uf is in Vg, then f≤g, so every Uf’ containing Uf must be such that f’≤f (that was Fact F of last time), whence Uf’ is in Vg, too. We consider any directed family D of Scott-open subsets of Lfan whose supremum is in Vg, and we wish to show that D intersects Vg. If Lfan ∈ D, then some element of D (Lfan itself) is in Vg, and we are done. Hence we assume that Lfan is not in D. It cannot be the case that D only contains the empty set, since sup D would be the empty set, and ∅ is not in Vg. Then we may assume that D does not contain the empty set, without loss of generality: removing the empty set yields a cofinal subfamily, which will in particular be directed and have the same supremum. This way, we may assume that D is a directed family of sets of the form Ufi, i ∈ I. Using the order-isomorphism with (N → N)op plus extra top and bottom elements (Fact F of last time), its supremum is Uf where f is the pointwise infimum of (fi)i ∈ I.
By assumption, Uf is in Vg, so f≤g. For each one of the elements m of the domain of g, we can then find an index i ∈ I such that fi(m)≤g(m); indeed, the family (fi(m))i ∈ I is well-founded, namely it reaches its least element. Since dom g is finite and (fi)i ∈ I is directed (with respect to ≥), we can take the same i ∈ I for every m ∈ dom g; namely, for every m ∈ dom g, fi(m)≤g(m). For every natural number m outside dom g, we have g(m)=ω, so fi(m)≤g(m) as well. Therefore fi≤g. This terminates our argument that Vg is Scott-open.
Second, O(Lfan) is trivially Scott-open, and {Lfan} is Scott-open, too: given any directed family of Scott-open subsets (Ui)i ∈ I of Lfan whose union is in {Lfan}, namely whose union is equal to Lfan, or equivalently, whose union contains ⊥, some Ui must contain ⊥ already, namely Ui=Lfan.
Finally, we need to show that the set Vg, {Lfan} and O(Lfan) form a base of of the Scott topology on O(Lfan). Let U ∈ O(Lfan), and let W be a Scott-open subset of O(Lfan) such that U ∈ W. If U=Lfan, then U ∈ {Lfan} ⊆ W. If U=∅, then W=O(Lfan). It remains to see what happens when U = Uf for some function f from N to N. For every k ∈ N, let gk : N → Nω map every natural number m<k to f(m), and all others to ω. Clearly, U = Uf ∈ Vgk for every k ∈ N (since f≤gk), and we claim that Vgk ⊆ W for some k ∈ N; this will finish the proof.
Let us assume that Vgk is not included in W for any k ∈ N. For every k ∈ N, there is an element of Vgk that is not in W. That element cannot be Lfan, since Lfan is in W (W is non-empty since it contains U, and upwards-closed, hence contains the largest element of O(Lfan)). It cannot be the empty set either, since the empty set is not in Vgk. Hence it must be equal to Ufk for some function fk : N → N. For the record, we will to remember that: (a) Ufk ∈ Vgk and: (b) Ufk ∉ W.
Let f’ : N → N map every number m to max(f(m), f0(m), …, fm(m)). Then f≤f’, and: (c) fk(m)≤f’(m) for every m≥k.
For every k ∈ N, we now define f’k : N → N as mapping every number m<k to f(m) and every number m≥k to f’(m). Then f’ = f’0 ≥ f’1 ≥ … ≥ f’k ≥ …, and infk ∈ N f’k = f. Using the order-isomorphism with (N → N)op plus extra top and bottom elements (Fact F of last time), Uf’ = Uf’0 ⊆ Uf’1 ⊆ … ⊆ Uf’k ⊆ …, and supk ∈ N Uf’k = Uf. Since the latter is in W, which is Scott-open, some Uf’k is in W.
We claim that f’k ≥ fk. For every m≥k, f’k(m) = f’(m) ≥ fk(m), by (c) (see a few lines back). For every m<k, f’k(m) = f(m); since Ufk is in Vgk (by (a)), fk≤gk, so fk(m)≤gk(m), but since m<k and by definition of gk, gk(m)=f(m); so f’k(m) = f(m) = gk(m) ≥ fk(m).
We can now conclude: f’k ≥ fk, so by the usual isomorphism (Fact F of last time), Uf’k is included in Ufk; since Uf’k is in W and W is upwards-closed, Ufk is in W, too. But that contradicts the definition of Ufk, namely (b). Therefore Vgk ⊆ W for some k ∈ N, as promised. ☐
As a side remark, the base given in Proposition D is countable. Therefore, and while Lfan is not first-countable hence not second-countable, O(Lfan) is second-countable in its own Scott topology, as was noted by Hertling.
Lfan is consonant
A space X is consonant if and only if for every open subset U of X, for every Scott-open neighborhood W of U in OX, there is a compact saturated subset Q of X such that Q ⊆ U and every open neighborhood of Q in X belongs to W. I have talked quite a few times about that property. Let me recall that every locally compact space is consonant (Exercise 5.4.12 in the book), and that every regular Čech-complete space is consonant (the Dolecki-Greco-Lechicki theorem, see Exercise 8.3.4 in the book).
Lemma E. Every sober space X such that OX has a base of Scott-open subsets U that are filters (viz., [upwards-closed, non-empty and] such that the intersection of any two elements of U is in U) is consonant.
Proof. Let U be an open subset of X, and W be a Scott-open neighborhood of U in OX. By assumption, there is a Scott-open neighborhood U of U included in W that is a filter. By the Hofmann-Mislove theorem (Theorem 8.3.2 in the book), since X is sober, U is the collection of open neighborhoods of some compact saturated subset Q of X. This is the desired set Q. ☐
The sets Vg, with g ∈ FF, are filters. Given any two open subsets in Vg, if one is equal to the whole of Lfan, then their intersection is the other one, which is in Vg; otherwise, they are of the form Uf and Uf‘ for some functions f, f’ : N → N such that f, f’ ≤ g, and by the order-isomorphism with (N → N)op plus a top and a bottom element (Fact F of last time), their intersection is Umax(f,f’); since max(f,f’)≤g, Umax(f,f’) is also in Vg. It is easy to see that {Lfan} and O(Lfan) are filters, too. Those form a base of the Scott topology on O(Lfan), by Proposition D. Since Lfan is sober (Lemma A), we can apply Lemma E, and we obtain the following.
Proposition F. Lfan is consonant in its Scott topology.
The compact saturated subsets of Lfan
Given any function g ∈ FF, let Qg be the subset of Lfan consisting of ⊤ plus all pairs (m, n) where m ∈ dom g and n≥g(m). Hence Qg is defined just like the Scott-open set Uf, except that g is a slightly different kind of function; also, while both Qg and Vg are indexed by the same kind of functions g, Vg was a Scott-open subset of O(Lfan), while Qg will be a compact saturated subset of Lfan. There is a link, though: Vg is the collection of open neighborhoods of Qg in Lfan.
Here is an illustration of what Qg looks like, with a function g of domain {0, 2}:
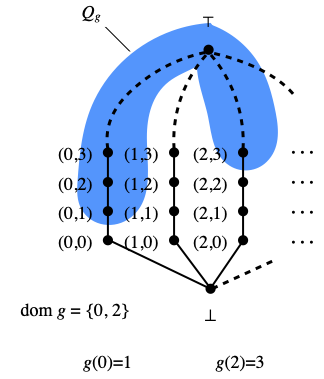
Lemma G. The compact saturated subsets of Lfan are the empty set, the whole space Lfan and the sets of the form Qg, where g ranges over FF. They are all finitary compact, namely, upward closures of finite sets.
Proof. All those sets—the empty set, Lfan, Qg—are finitary compact; notably, Qg is the upward closure of the finite set of points (m, g(m)), m ∈ dom g if dom g is non-empty, and is the upward closure of ⊤ if dom g is empty. Therefore they are all upwards-closed and compact.
Conversely, let Q be a non-empty proper compact saturated subset of Lfan. Being proper, it does not contain ⊥. Since it is non-empty, it contains ⊤. For every m ∈ N, let us say that column m is empty if and only if Q contains no pair (m, n) for any n (but for this particular value of m); it is non-empty otherwise.
Let I be the set of indices m ∈ N such that column m is non-empty. There is a smallest natural number n such that (m, n) is in Q, and we call it g(m). For every number m outside I, we let g(m) ≝ ω. This defines a function g from N to Nω, whose domain is I.
By way of contradiction, let us assume that I is infinite. We build a function fm : N → N, one for each m ∈ I, which maps m to g(m), every m’ ∈ I–{m} to g(m’)+1, and all other indices to some arbitrary value, say 0. The Scott-open sets Ufm, m ∈ I, form an open cover of Q: every point of Q (other than ⊤, which is in any Ufm anyway—and there is such a Ufm, since I is non-empty) is of the form (m, n) with n≥g(m)=fm(m), hence is in Ufm. That open cover has no strict subcover: if we remove any set Ufm (m ∈ I) from the cover, the point (m, f(m)) of Q fails to be in any Ufm’, m’ ∈ I–{m}. Since I is infinite, this contradicts the fact that Q is compact.
Hence I is finite. Therefore g is in FF, and it is easy to see that Q=Qg. ☐
Fact H. For all g, g’ ∈ FF, Qg ⊇ Qg’ if and only if g ≤ g’.
With this characterization, we retrieve some results we have already obtained, in a more concrete fashion:
- Lfan is not core-compact. Indeed, Lfan is sober (Lemma A) and in that case, core-compactness is equivalent to local compactness (see Theorem 8.3.10 in the book). But the only compact saturated subset of Lfan with non-empty interior is Lfan itself. Indeed, the proper compact saturated subsets are of the form Qg, and none contains any Scott-open subset of the form Uf. Explicitly, Uf ⊆ Qg if and only if f ≥ g, and that cannot happen for an N-valued function f and a function g in FF.
- Lfan is coherent. This is a consequence of the fact that Lfan is a maximal limit space, which we have seen in Proposition C. More directly, the intersection of Qg and of Qg’ is equal to Qh, where h maps every m ∈ N to max(g(m), g’(m)).
The Smyth hyperspace of Lfan
Last time (Corollary C), we had mentioned that, because Lfan has the Chen-Kou-Lyu property, the Scott topology coincides with the lower Vietoris topology on the Hoare hyperspace H(Lfan). Having explored the shape of compact saturated subsets of Lfan, we can now investigate the other classical hyperspace, the Smyth hyperspace.
The Smyth hyperspace QX of a space X is the space of all compact saturated subsets of X, with the upper Vietoris topology: its basic open subsets are of the form ☐U ≝ {Q ∈ QX | Q ⊆ U}, where U ranges over the open subsets of X. QX is a T0 space, whose specialization ordering is reverse inclusion. With what we know about the compact saturated subsets of Lfan, we can show the following.
Proposition I. The upper Vietoris topology coincides with the Scott topology of ⊇ on Q(Lfan) (where Lfan is given its Scott topology).
Proof. First, every upper Vietoris open subsets of Q(Lfan) is Scott-open. Indeed, since Lfan is sober (Lemma A), hence well-filtered (Proposition 8.3.5 in the book), the supremum of any directed family (Qi)i∈I in Q(Lfan) is its intersection ∩i∈I Qi (Proposition 8.3.25 in the book), and ∩i∈I Qi is in a basic open set ☐U if and only if some Qi is in ☐U already (this is well-filteredness).
Second, let U be any Scott-open subset of Q(Lfan). For every Q ∈ U, we will find a Scott-open subset V of Lfan such that Q ∈ ☐V ⊆ U. By Lemma G, Q may have one of three possible forms. If Q=Lfan, then U is the whole of Q(Lfan), since U is upwards-closed and Q is the least element of Q(Lfan); then we may define V as Lfan. If Q is empty, then we may take V ≝ ∅. In the case that remains, Q = Qg for some unique g ∈ FF, and we build a sequence of functions gn in FF by induction on n ∈ N, as follows. The invariants we will maintain are:
- (A) Qgn is in U;
- (B) the domain of gn+1 is equal to the domain of gn plus the one-element set {kn}, where (kn)n∈N is a fixed enumeration without repetition of those natural numbers that lie outside the domain of g.
We start by defining g0 as g. Given that we have defined gn, we observe that the functions gn[kn ↦ m], defined just as gn except that kn (which is outside the domain of gn) is mapped to the natural number m, form a monotone sequence when m varies over N, and that their supremum is gn. Through the order-isomorphism stated in Fact H, Qgn is the supremum of the monotone sequence of compact saturated sets Qgn[kn ↦ m], m ∈ N. Since Qgn is in U and U is Scott-open, Qgn[kn ↦ m] is in U for some m ∈ N. We pick one such m, for example the least one, and we define gn+1 as gn[kn ↦ m]. Hence Qgn+1 is in U (see (A)) and (B) is true.
Now that we have defined the functions gn, we define f : N → N as the pointwise infimum of gn, n ∈ N. There is a simpler way of describing f: for every m ∈ N, gn(m) may be equal to ω for small values of n, but for any n large enough, gn(m) will be the same natural number, independently of n; and that number is f(m). This is a consequence of (B).
We let V ≝ Uf. This is Scott-open in Lfan. Also, Q = Qg is included in Uf, hence is an element of ☐V. Indeed, ⊤ is in Uf, and all the other elements of Qg are pairs (m, n) of natural numbers with n≥g(m); since n is a natural number, g(m)≠ω, so m is in the domain of g=g0, and therefore g(m)=f(m), whence n≥f(m).
Finally, we claim that ☐V ⊆ U. Let Q’ be any element of ☐V. Q’ cannot be the whole of Lfan, since otherwise ⊥ would be in Q’, hence in V = Uf, and that is impossible. If Q’ is empty, then certainly it is in U, because U is upwards-closed, non-empty (U contains Q) and therefore contains the top element of Q(Lfan), which is the empty set. Finally, and using Lemma G, the only case that remains is that Q’ would be of the form Qg’ for some function g’ in FF. Since Q’ = Qg’ ⊆ V = Uf, every pair (m, n) such that n≥g’(m) satisfies n≥f(m), so g’≥f. Since the domain dom g’ of g’ is finite, and since the domains of the functions gn form a monotone sequence of sets dom g ∪ {k0, …, kn–1} as n varies, and whose union is the whole of N, it must be the case that dom g’ ⊆ dom gn for some n large enough. But f coincides with gn on dom gn, so g’≥f entails that g’≥gn: for every m in dom g’ ⊆ dom gn, g’(m)≥f(m)=gn(m), and for every m outside dom g’, g’(m)=ω. By Fact H, Qg’ lies above (namely, is included in) Qgn. But, by (A), Qgn is in U. Since U is upwards-closed, Qg’ (= Q’) is in U. Since Q’ is arbitrary in ☐V, this shows that ☐V ⊆ U. ☐
Xiaoyong Xi calls conformal any well-filtered topological space X such that the upper Vietoris and Scott topologies of ⊇ coincide on QX. (I am not sure where this comes from. He gave me some names for the inventors of the notion, but I was unable to find a corresponding reference.)
One can read Lemma 8.3.26 in the book as saying that every well-filtered, locally compact space is conformal. A theorem due to Xiaoquan Xu and Zhongqiang Yang [9, Corollary 5.9] states that every well-filtered, first-countable space such that every compact saturated subset has countably many minimal elements is conformal. Here Lfan is neither core-compact nor first-countable, but is conformal nonetheless. (Note that its compact saturated subsets not only have countably many, but even finitely many minimal elements.)
I will conclude by the following summary: Lfan is an example of a conformal space in its Scott topology, which is not first-countable and not core-compact, but is a consonant, maximal limit space and a complete lattice.
- Yu Chen, Hui Kou, and Zhenchao Lyu. Two topologies on the lattice of Scott closed subsets. Topology and its Applications, 306, 107918, 2022.
- Hualin Miao, Xiaoyong Xi, Qingguo Li, and Dongsheng Zhao. Not every countable complete distributive lattice is sober, Mathematical Structures in Computer Science 33(9):809–831, October 2023. arXiv version arXiv:2205.00250v1 [math.GN], 30 Apr 2022.
- Xiaoquan Xu, Chong Shen, Xiaoyong Xi, and Dongsheng Zhao. First countability, ω-well-filtered spaces and reflections. Topology and its Applications, 279, 107255, 2020.
- Peter Hertling. Topological properties of the binary supremum function. Semigroup Forum 104:618–646, 2022.
- Klaus Keimel and Jimmie Lawson. Measure extension theorems for T0-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
- Douglas N. Hoover. Maximal Limit Spaces, Powerspaces, and Scott Domains. Proceedings of the 11th International Conference on Mathematical Foundations of Programming Semantics (MFPS), New Orleans, Louisiana, USA. Electronic Notes in Theoretical Computer Science 1:253–272, 1995.
- Reinhold Heckmann. An upper power domain construction in terms of strongly compact sets. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds) Mathematical Foundations of Programming Semantics. MFPS 1991. Lecture Notes in Computer Science, vol 598. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-55511-0_14
- Andrea Schalk. Algebras for Generalized Power Constructions. PhD Thesis, TU Darmstadt, 1993.
- Xiaoquan Xu and Zhongqiang Yang. Coincidence of the upper Vietoris topology and the Scott topology. Topology and its Applications 288, February 2021.

— Jean Goubault-Larrecq (June 20th, 2024)
