Let me briefly review what we have seen last time. The Skula topology on a topological space X is generated by the crescents U–V, where U and V are open in X. A theorem due to R.-E. Hoffmann states that X is Noetherian in its original topology if and only if it is compact Hausdorff in its Skula topology (see [1], or Exercise 9.7.16 in the book).
Now a Skula space is a topological space obtained by taking a topological space and giving it its Skula topology. A. Dow and S. Watson investigated the question when a compact space is Skula [2]; note that the difficulty is that the underlying Noetherian topology is unknown. However, using Hoffmann’s theorem, we have proved the following theorem of theirs: given a compact (not necessarily Hausdorff) space X, X is Skula if and only if it has a clopen selector η.
A clopen selector is, by definition, a map η : X → CO(X), where CO(X) is the collection of clopen subsets of X, satisfying the following conditions:
- (DW0) for every point x of X, x ∈ η(x);
- (DW1) for all points x and y, x ∈ η(y) and y ∈ η(x) together imply x=y;
- (DW2) for all points x and y, if x ∈ η(y) then η(x) ⊆ η(y).
It is equivalent to give a clopen selector η or a partial ordering ≤ on X that is pointwise-clopen, in the sense that the downward closure ↓x of every point x with respect to ≤ is clopen. Given a clopen selector η, we have x≤y if and only if x ∈ η(y), and conversely, given a pointwise-clopen partial ordering ≤, we obtain a clopen selector as the function that maps every point x to ↓x.
Dow and Watson then noticed that every compact T0 Skula space is scattered (and necessarily Hausdorff). A scattered space is a space whose only dense-in-itself subset is the empty set; a subset D of X is dense-in-itself if it has no isolated point. Now one may enquire whether the converse holds: is every compact Hausdorff scattered space Skula?
Last time, I described Dow and Watson’s argument justifying that every compact Hausdorff scattered space of height at most 3 is Skula. This proceeds by explicitly constructing a clopen selector. This time, we will show that this is the best we can say: there is a compact Hausdorff scattered space of height 4 that is not Skula [2, Example 1]: there is absolutely no (necessarily Noetherian) topology whose Skula topology would give back the given compact Hausdorff scattered topology.
Before we do so, let me notice that it is pretty obvious that there are compact Hausdorff spaces that are not Skula. For example, [0, 1] with its usual metric topology cannot be Skula, because it is not scattered. The difficulty is in finding a compact Hausdorff scattered space that is not Hausdorff.
Right. I have just mentioned the (scattering) height of a scattered space. I will not need the full definition; see this post if you are curious. For low heights, the following, which I have already said last time, will be enough.
- Given a compact subspace K of a space X, let K’0 ≝ K, and let K0 be the set of all isolated points of K. If K0 is empty, then the scattering height of K is 0.
- K’1 ≝ K’0–K0 is another non-empty compact subset of X. Let K1 be its set of isolated points. If K1 is empty (and K0 is not), then the scattering height of K is 1.
- K’2 ≝ K’1–K1 is another non-empty compact subset of X. Let K2 be its set of isolated points. If K2 is empty (and K0, K1 are non-empty), then the scattering height of K is 2.
- K’3 ≝ K’2–K2 is another non-empty compact subset of X. Let K3 be its set of isolated points. If K3 is empty (and K0, K1, K2 are non-empty), then the scattering height of K is 3.
- And so on.
By definition, a subspace K of scattering height 3 that is scattered is such that K3 is empty, and also K is the (disjoint) union of K0, K1, and K2. Here is how such a space looks like. All the points of K2 are isolated inside K2, but are limits of nets of points from K1; this is what the sequences of dots (• • • ·······) on the K1 level mean. The points of K1 are themselves isolated in K1 ∪ K2 (= K’1), but are limits of nets of points from K0. All the involved nets are shown as completely separate here, but in general they can share points.
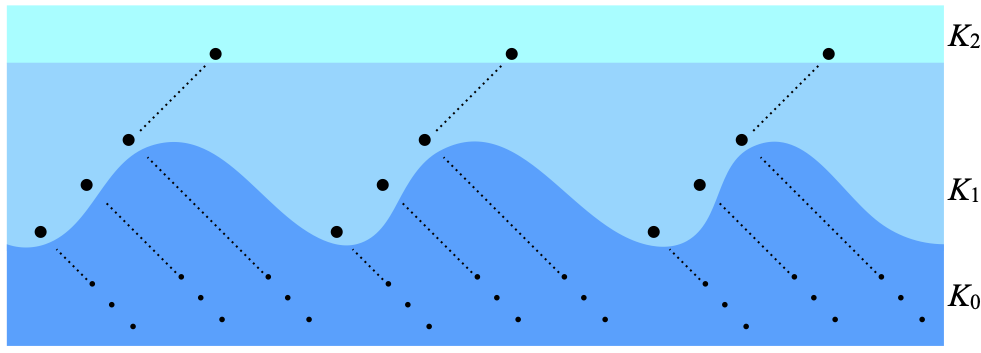
A compact Hausdorff scattered space of height 4 has just one extra layer K3. The counterexample that Dow and Watson build has just one point in K3. Then K2 will be infinite, in fact even uncountable; this should be contrasted with the fact that in a compact Hausdorff scattered space of height 3, K3 is always finite (and we used that fact last time).
Almost disjoint families
The first thing we need to do is an exercise in infinite combinatorics, specifically on almost disjoint families of subsets of N. (N is the set of natural numbers.)
Two subsets A and B are almost disjoint if and only if A ∩ B is finite (instead of empty if A and B were disjoint). A family E of subsets of N is almost disjoint if and only if every pair of distinct sets A and B in E are almost disjoint.
One may wonder how large the cardinality of an almost disjoint family E of subsets of N can be. Surely it cannot be larger than c, the cardinality of the powerset P(N) of N. This is the cardinality of the continuum, whence the letter c. Another notation for this cardinal number is 2ℵ0, where ℵ0 is the cardinality of N. This is also the cardinality of the set R of real numbers, or of the set NN of all functions (all of them, not just the monotonic or the Scott-continuous ones) from N to N.
It is also easy to see that there are almost disjoint families that are countable infinite. For example, the collection of one-element subsets {n} of N is a countably infinite disjoint (hence almost disjoint) family. Because “almost disjoint” is almost “disjoint”, one might guess that all almost disjoint families of subsets of N would be countable, similarly, but that is not true, as we see.
Proposition. There is an almost disjoint collection E of infinite subsets of N, whose cardinality is c.
Proof. There are many possible proofs of this, and my preferred one goes as follows. We build a tree whose vertices are the non-zero natural numbers, and where each vertex n (hence, n is a number such that n≥1) has two sons, 2n and 2n+1. See the following picture.
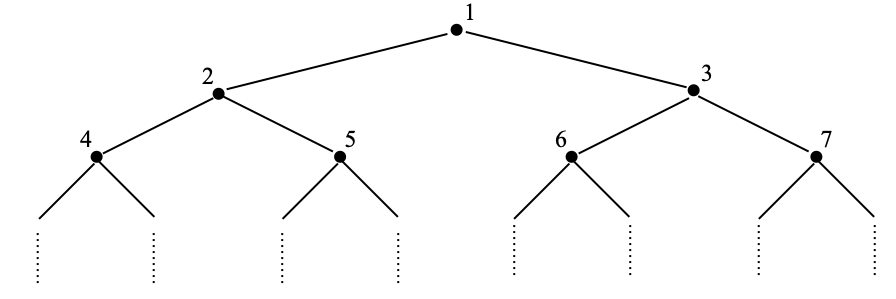
The picture makes it clear that we have just produced a complete binary tree: an infinite tree whose vertices all have two sons. A branch starts from 1, then goes to one of its sons, then to one if its son’s sons, and so on, for example 1, 2, 5, etc. (A branch never stops.) A branch is entirely determined by the set of choices among the two sons we make at each step; hence there are exactly as many branches as there are maps from N to {left, right}; equivalently, as there are subsets of N, and there are c of them.
Now, for each branch of that tree, let us collect the numbers that appear as vertices on that branch: for example {1, 2, 5, …}. Since vertices are numbers (≥1), we can equate any branch with the collection of its vertices, which is a subset of N. It remains to observe that any two distinct branches are almost disjoint. And indeed, given two distinct branches A and B, they will start with a common, finite prefix, and then they will take distinct choices of sons (left/right) after that finite prefix. The key is that any element after that choice is made cannot be both in A and in B, so A and B only share their finite prefix. For example, if A = {1, 2, 4, …} (whatever the rest is) and B = {1, 2, 5, …} (whatever the rest is, again), then A ∩ B = {1, 2}.
This can be proved formally as follows. The collection E consists of those infinite subsets As of N, where s ranges over the infinite sequences of bits, namely the maps from N to {0, 1}; As is defined as the collection of numbers which, written in binary, consist of a 1 followed by a finite prefix of s. For example, {1, 2, 5, …} is the collection of numbers that, written in binary, are of the form 1, 10, 101, etc. (the binary notations of 1, 2, 5, etc.), and typically come from an infinite sequence such as 011101010100110… by taking finite prefixes and adding a 1 to the front. If As and At are two distinct such sets, then the sequences s and t must be different, and there must therefore be a position n such that s(n)≠t(n), say s(n)=0 and t(n)=1. Let us choose n minimal with this property, so s(0), …, s(n–1) and t(0), …, t(n–1) form the same sequence w of n bits. Now all the elements of As whose binary notation have length ≥n+2 are of the form 1w0…, while all those from At of length ≥n+2 are of the form 1w1…, and are therefore distinct. It follows that As ∩ At consists exactly of the numbers ≥1 which have a binary expansion that is a prefix of the finite sequence 1w, and there are exactly n of them. ☐
Let us fix E as above. There is a one-to-one map s ↦ As from P(N) to E. That stems from cardinality considerations, but the proof I gave above actually provides such a map, explicitly: simply equate the subsets s of N with infinite sequences of bits; for example, {4, 7, 9} is 0000100101000…, with a 1 at positions 4, 7, and 9.
Since the space NN of all functions from N to N also has cardinality c, there is another one-to-one map s ↦ fs from P(N) to NN.
Dow and Watson’s counterexample, step 1
Here is how Dow and Watson build their counterexample. This takes 3 steps. We start with N × Nω (Dow and Watson use Nω × N, but the pictures will be nicer if I use N × Nω), with a suitable Hausdorff topology; this will be scattered of height 2. Then we add the whole of P(N) as a closed discrete space; the result is scattered of height 3. Finally, we take the Alexandroff compactification, adding a final point at infinity ∞, which will be the only point at height 4.
Right, so let us start with step 1.
We equip N with the discrete topology. The space Nω is the Alexandroff compactification of N, namely: the elements of Nω are the natural numbers plus an extra element ω, and the open subsets of Nω are:
- all the subsets of N (namely, all the subsets of Nω that do not contain ω),
- plus all the sets of the form Nω–A, where A is a finite subset of N (namely, subsets of Nω that do contain ω, but then must contain all natural numbers except finitely many).
Then N × Nω is the topological product of those two spaces. This is a Hausdorff space. Its set of isolated points is N × N, and if you remove them, you will be left with an isomorphic copy of N. Hence N × Nω is scattered, of scattering height equal to 2.
Dow and Watson’s counterexample, step 2: adjoining a copy of P(N)
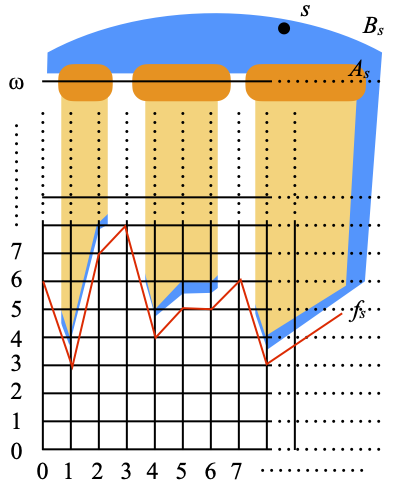
We form the disjoint union of N × Nω with P(N), with a very specific topology. In order to define it, we must be first define an important collection of sets. For every s ∈ P(N), let Bs be the set consisting of:
- s itself;
- the pairs (i, j) of natural numbers (hence j<ω) such that j>fs(i);
- and (i, ω), where i ∈ As.
(Remember that As enumerates an almost disjoint family of subsets of N, and that fs enumerates all the functions from N to N.) Hence Bs is the union of {s}, plus the dark orange region below it (a copy of As inside the top row of N × Nω) and of the light orange region consisting of all points strictly above the graph of fs in N × N. The total is tentatively depicted as a kind of blue background.
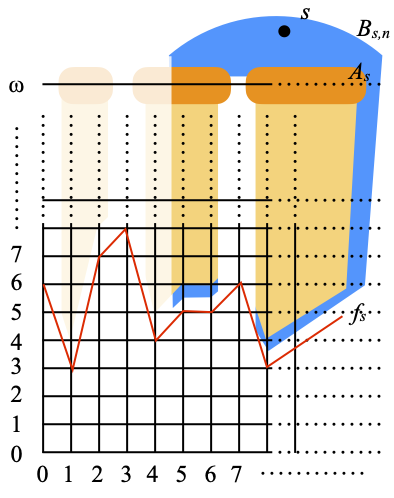
Let us call X the space obtained as the disjoint union of N × Nω with P(N). We generate its topology from the following base:
- all the open subsets of N × Nω;
- for each point s of P(N), the sets Bs,n ≝ Bs – {(i, j) ∈ N × Nω | i<n}, where n ranges over N: in other words, Bs,n is obtained from Bs by erasing all the points in columns 1, …, n–1; see the picture below, where n=5, and the part that was erased still appears as a translucent shadow.
This is a base indeed, because it is closed under binary intersection:
- Bs,m ∩ Bs,n = Bs,max(m,n);
- if s≠t in P(N), then Bs,m ∩ Bt,n does not contain any point in P(N), hence is a subset of N × Nω, and we claim that it is open in N × Nω; indeed, it is a union of columns {i} × Vi, where Vi ≝ {j ∈ Nω | j>fs(i), ft(i)}, for i in As ∩ At larger than or equal to both m and n; {i} is open in N (whose topology is discrete) and Vi is open in Nω, since its complement is finite;
- the intersection of any two open subsets of N × Nω is open in N × Nω;
- finally, the intersection of Bs,n with an open subset U of N × Nω is open in N × Nω. In order to show this, let (i, j) be any point of Bs,n ∩ U; it suffices to show that (i, j) has an open neighborhood in N × Nω that is included in Bs,n ∩ U. If j<ω, then {(i, j)} is open in N × Nω, included in Bs,n ∩ U, and contains (i, j). If j=ω, then there is an open rectangle E × (Nω–A) containing (i, j) and included in U, where E is a subset of N and A is a finite set of natural numbers. Let m be a natural number strictly larger than all the elements of A and strictly larger than fs(i): then {i} × (Nω–{0, 1, …, m–1}) is an open neighborhood of (i, j) in N × Nω that is included in Bs,n (because m>fs(i)—we have i≥n because (i, j) is in Bs,n to start with) and also in E × (Nω–A), hence in U.
We note the following.
Lemma A. In X, Bs is both compact and open.
Proof. First, it is open because it is equal to Bs,0. In order to show that it is compact, we use Alexander’s subbase lemma (Theorem 4.4.29 in the book): we take any cover of Bs by basic open sets, and we show that a union of finitely many of them already covers Bs. In this cover, we find three kinds of sets:
- sets of the form Bs,n, with varying n but the same s,
- sets of the the form Bt,m with t≠s and various values of m,
- and open subsets of N × Nω.
Also, since s is in Bs, there must be at least one set of type 1. We take the set of type 1 with the smallest n. This exists because N is well-founded and totally ordered. Then that set, which we will simply write as Bs,n in the sequel, contains all the other sets of type 1.
The points of Bs that remain, namely those that are not in Bs,n, form a finite union of columns {i} × Ci, for various values of i among {0, 1, …, n–1}, and where each Ci is equal to {j ∈ Nω | j>fs(i)}. We claim that each such column, which must be covered by sets of types 2 and 3, is covered by finitely many of them. Since there are only finitely many such columns, this will show that we can cover Bs by Bs,n plus finitely many sets of types 2 and 3.
- If sets of type 3 suffice to cover a column {i} × Ci, then only finitely of them cover that column: (i, ω) must be in one of those sets of type 3, call it V; by definition of the topology on N × Nω, V must contain an open rectangle of the form E × (Nω–A), where E is a subset of N containing i and A is a finite set of natural numbers; and the points in {i} × Ci minus V must then all be of the form (i, j) with j ∈ A, hence are covered by finitely many of the remaining sets of type 3.
- Otherwise, the cover contains at least one set Bt,m that contains at least one point of the column {i} × Ci. That set Bt,m must contain all the pairs (i, j) with i as given, and with j>ft(i). The remaining points satisfy j≤ft(i), so there are only finitely many of them. Hence we can cover {i} × Ci by Bt,m, plus as many sets of types 2 and 3 as needed to cover the finitely many remaining points of the column. ☐
Lemma B. X is Hausdorff.
Proof. One can separate any two distinct points of N × Nω by open subsets because N × Nω is Hausdorff and because every open subset of N × Nω is also open in X.
Given a point (i, j) in N × Nω and a point s in P(N), we can separate them by the open sets {i} × N and Bs,n, where n is any natural number strictly larger than i.
Finally, we can separate two distinct points s and t of P(N) as follows. Since As and At are almost disjoint (this is where we are using this!), their intersection is finite, so we can find a natural number n that is strictly larger than any number in that intersection. Then Bs,n and Bt,n are disjoint: any point in the intersection would be a pair (i, j) where i is in As, in At, and larger than or equal to n, and that is impossible. Additionally, Bs,n and Bt,n are open neighborhoods of s and t respectively. ☐
Lemma C. X is locally compact.
Proof. Since X is Hausdorff, by Lemma B, it suffices to find a compact neighborhood around each point (Proposition 4.8.7 in the book). Around (i, j) in N × N, {(i, j)} works great. Around (i, ω), {i} × Nω is compact, being the product of two compact sets, and is also open (being an open rectangle). Around s in P(N), Bs itself is compact and open, by Lemma A. ☐
Lemma D. X is scattered, of scattering height equal to 3.
I will let you check that by yourself: the isolated points of X are the same as with N × Nω, namely those of N × N; in what remains, the isolated points are the pairs (i, ω); and once we have removed the whole of N × Nω, finally all the points of P(N) become isolated.
Dow and Watson’s counterexample, step 3: taking the Alexandroff compactification and concluding
Since X is locally compact and Hausdorff, by Lemmata B and C, its Alexandroff compactification α(X) is compact Hausdorff (Exercise 4.8.9 in the book). This process adds only one new point to X, which I will write as ∞, and then, as you may check, this makes α(X) scattered, of scattering height equal to 4.
It is finally time to argue that α(X) cannot be Skula. Let us imagine it is. Then it has a clopen selector η : α(X) → CO(α(X)), and it is easier to remember that, for each point x of α(X), η(x) is equal to the downward closure ↓x with respect to some ordering ≤, which must be point-clopen.
Lemma E. (Assuming that α(X) has a clopen selector η, with associated pointwise-clopen ordering ≤.) For every natural number i, there are only finitely many natural numbers j such that (i, j) ≰ (i, ω); in other words, such that (i, j) is not in the clopen set η(i, ω).
Proof. Since η(i, ω) is open and contains (i, ω), it must contain a basic open set U containing (i, ω). We claim that there are only finitely many values of j such that (i, j) is not in U, and that will imply that there are only finitely many values of j such that (i, j) is not in η(i, ω).
If U is of the form Bs,n and contains (i, ω), then it must contain every (i, j) such that j > fs(i), and there are only finitely many values of j that fail to satisfy that inequality.
If U is a basic open neighborhood of (i, ω) that is open in N × Nω, then it contains an open rectangle of the form {i} × (Nω–A), where A is a finite subset of N, and then again we only have a finite set (namely, A) of values to choose from for j. ☐
For every natural number i, Lemma E allows us to define the following function f.
Definition (f). (Assuming that α(X) has a clopen selector η, with associated pointwise-clopen ordering ≤.) For every i ∈ N, let f(i) be any number that exceeds all the finitely many numbers j such that (i, j) ≰ (i, ω).
By contraposition, we deduce that:
Fact F. (Assuming that α(X) has a clopen selector η, with associated pointwise-clopen ordering ≤.) For all natural numbers i and j, if j > f(i) then (i, j) ≤ (i, ω).
Let s be any element of P(N) such that fs(i) > f(i) for every natural number i. That certainly exists, since the maps fs enumerate all the maps from N to N. For now, s is fixed, but we will make it vary later on.
The element s is a point of X, hence of α(X). (Still assuming that η is a clopen selector,) the clopen set η(s) is an open neighborhood of s in α(X). Since the only basic open neighborhoods of s are those of the form Bs,n, for some n in N, one of them must be included in η(s). (Remember that they are basic, not just subbasic, because they are closed under binary intersections.) But Bs,n contains all the elements of As × {ω}, except for finitely many (namely, except for those (i, ω) such that i<n). Here is the situation:

Let Is be the set of natural numbers i in As such that (i, ω) is in η(s). (The indices of the columns in the blue region, partially hidden by the light orange zones, in the picture above.)
Lemma G. The set Is has the following three properties:
- Is ⊆ As;
- Is and As differ by finitely many elements only;
- for every i ∈ Is, η(i, ω) is included in η(s).
Proof. Item 1 is by definition. For item 2, As–Is consists of those elements i in As such that (i, ω) is not in η(s); Lemma E tells us that there are only finitely many of those. For item 3, we use property (DW2), namely, that for all points x and y, if x ∈ η(y) then η(x) ⊆ η(y); or, if you prefer, the elements of η(i, ω) are those elements x ≤ (i, ω), and since (i, ω) ∈ η(s), we have (i, ω) ≤ s, so that x ≤ s, equivalently x ∈ η(s). ☐
Next, we consider the set Es of all points (i, j) ∈ N × N such that i ∈ Is and j > f(i). This is depicted as the union of the vertical rounded rectangles below. We recall that fs(i) > f(i) for every natural number i. Hence Es consists of all the points in the light orange area in the picture above (and reproduced below), plus a few more below them shown as purple, vertical blobs; actually, with at least one more point in each blob, namely at one more point per orange column, and there are infinitely many such columns.
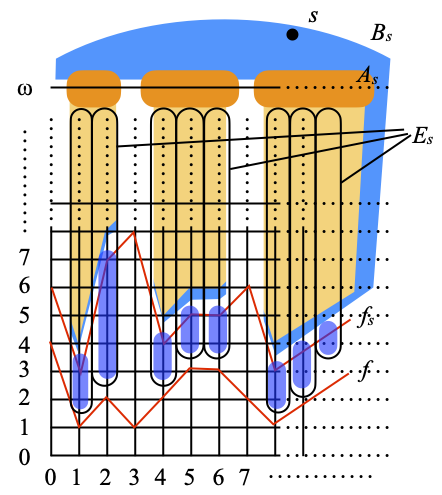
Let us use clα to denote closure in α(X). We claim the following.
Lemma H. The cluster points of Es, namely the points of clα(Es)–Es, are among the points (i, ω) with i ∈ Is (at scattered height 2), or s (at height 3), or ∞ (at height 4).
I do not mean that all of them should be cluster points of Es, just that the cluster points must be among them.
Proof. First, imagine that (i, ω) is a cluster point of Es (at height 2). If i is not in Is, then {i} × Nω is an open neighborhood of (i, ω) that does not intersect Es, so (i, ω) cannot be in clα(Es). Therefore i ∈ Is.
Second, imagine that t ∈ P(N) is a cluster point of Es (at height 3). If t≠s, then we use the fact that As and At are almost disjoint. (This is the second time we use that property.) There is a natural number n such that As and At have no element in common that is larger than or equal to n. Then Bt,n is an open neighborhood of t that has no column in common with Es, hence does not intersect it; so t is not in clα(Es). It follows that we must have t=s.
Finally, it may be that ∞ is a cluster point of Es, too, and that is fine; we do not need to prove anything here—and we address the question below anyway. ☐
Lemma I. ∞ is a cluster point of Es in α(X).
Proof. This means that every open neighborhood of ∞ intersects Es. By definition of the Alexandroff compactification, equivalently, this means that the complement of any compact subset of X must intersect Es, or equivalently that no compact subset of X can cover the whole of Es. Since we are working in Hausdorff spaces, all this is equivalent to the claim that the closure cl(Es) of Es in X (not its closure clα(Es) in α(X)) is not compact.
This closure cl(Es) is the intersection of clα(Es) with X. By Lemma H, cl(Es) is therefore equal either to Es, plus possibly some points of (i, ω) with i ∈ Is, plus possibly s. Hence it suffices to show that no such set is compact in X, or equivalently, to find an open cover of such a set that has no finite subcover.
This cover consists of:
- Bs (which is open, since it is equal to Bs,0),
- all the sets {i} × {f(i)+1, …, fs(i)}, where i ranges over Is (the indices of the columns of points in Es).
A picture being worth a thousand words, Bs is shown in blue below, and the sets of type 2 are the purple, vertical blobs shown below. Bs by itself covers s (if it is ever in cl(Es)) and all the points (i, ω) with i ∈ Is (in dark orange), plus all the points (i, j) ∈ N × N such that i ∈ Is and j > fs(i) (in light orange). The purple blobs cover the remaining points of Es, which satisfy the weaker condition j > f(i).
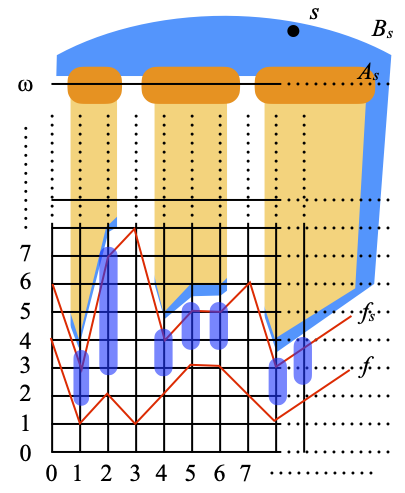
The set of type 1 (Bs) is disjoint from all the sets of type 2, which are all themselves pairwise disjoint. Each of the sets {i} × {f(i)+1, …, fs(i)} of type 2 contains at least one point of cl(Es); in fact, all the elements of {i} × {f(i)+1, …, fs(i)} are in Es, and there is at least one since fs(i) > f(i). It follows that all the subcovers of cl(Es) must contain all the sets of type 2. There are infinitely many of them because As is infinite, and therefore our cover has no finite subcover. ☐
Until now, we had fixed s. Making s vary, we have that for every s ∈ P(N) such that fs(i) > f(i) for every natural number i, the set Es has ∞ as a cluster point in α(X). We deduce the following.
Lemma J. (Assuming that α(X) has a clopen selector η, with associated pointwise-clopen ordering ≤.) For infinitely, even uncountably, many s ∈ P(N), ∞ ∈ η(s) (namely, ∞≤s).
Proof. Take any s such that fs(i) > f(i) for every natural number i. There are uncountably many such elements, because there are uncountably many functions from N to N that are pointwise strictly above f, and each of them is equal to fs for some s. Now, do you remember how we defined f, or better, what its main property is?
That was Fact F: for all natural numbers i and j, if j > f(i) then (i, j) ≤ (i, ω). Hence, for every i ∈ N, and letting j be any number larger than or equal to fs(i)—which is strictly larger than f(i)—, we must have (i, j) ≤ (i, ω). it is probably time for me to stress that ≤ is not the usual ordering on N × Nω, rather a hypothetic point-clopen ordering on α(X) with associated down-closure map η. Hence, alternatively, we have that every pair (i, j) of natural numbers with j larger than or equal to fs(i) is in η(i, ω), for every natural number i.
Do you also remember how we built Es? That was the set of all the points (i, j) ∈ N × N such that i ∈ Is and j > f(i). Let us forget about the latter part. All of those points are such that i ∈ Is. Do you remember what Is is? Probably not, but we had proved that η(i, ω) is included in η(s) for every i ∈ Is; that was Lemma G, item 3. Hence, for every point (i, j) in Es, i is in Is, (i, j) is in η(i, ω) by the last paragraph, and since η(i, ω) ⊆ η(s), (i, j) is in η(s).
Therefore Es is included in η(s). Since η(s) is clopen, hence closed, in α(X), we obtain that clα(Es) is also included in η(s). But Es has ∞ as a cluster point in α(X), by Lemma I, so ∞ is in clα(Es), and therefore ∞ is in η(s), as promised. ☐
In order to finally reach a contradiction and conclude, we observe that every open neighborhood of ∞ in α(X) contains all the points s ∈ P(N) except for finitely many. Indeed, an open neighborhood of ∞ must contain a possibly smaller open neighborhood of the form α(X)–K, where K is a compact subset of X. Now, K cannot contain more than finitely many points s ∈ P(N): otherwise the sets Bs (=Bs,0) where s ranges over K would form an infinite open cover of K that has no strictly smaller, hence no finite, subcover.
But η(∞) is an open neighborhood of ∞. Therefore s is in η(∞) for every s ∈ P(N) except for finitely many, namely s≤∞ for every s ∈ P(N) except for finitely many. Since for infinitely many s ∈ P(N), ∞≤s, by Lemma J, we obtain that for infinitely many s (except the finitely many for which s≤∞ fails) s=∞, which is impossible. Alternatively, for those s, ∞ ∈ η(s) and s ∈ η(∞), so s=∞ by (DW1), which is impossible.
We can now finally conclude.
Theorem [2, Example 1]. The space X is a compact Hausdorff scattered space, of scattering height 4, which has no clopen selector, and therefore is not Skula.
- Hoffmann, Rudolf-Eberhard. On the Sobrification Remainder sX–X. Pacific Journal of Mathematics, 83(1):145–156, 1979.
- Alan Dow and Stephen Watson. Skula spaces. Commentationes Mathematicae Universitatis Carolinae 31(1):27–31, 1990. ISSN: 0010-2628.
- Jean Goubault-Larrecq and Maurice Pouzet. A few characterizations of topological spaces with no infinite discrete subspace. Topology and its Applications 341, January 1st 2024, 108733.

— Jean Goubault-Larrecq (February 20th, 2024)
