Bitopological spaces, d-frames, and Jung-Moshier duality

Stone duality is an adjunction between the category Top of topological spaces and the category Loc of locales, namely the opposite of the category Frm of frames. You can learn about it in Section 8.1 of the book. Is there a similar-looking adjunction between the category biTop of bitopological spaces—namely, sets with two topologies instead of just one—and some category of order-theoretic structures? Well, yes, of course. I would not have asked the question otherwise. In fact, there are several of them, but I would like to talk about Jung and Moshier’s proposal [1], later further studied by Jakl in his PhD thesis [2].

It has been a long time since I wanted to talk about this, but the paper is too well-written. Mmh. All right, let me explain. I have known Achim Jung for some time, and he writes amazingly well. Whatever I can write, he writes it better than I can. In short, if I talk about [1], you had better read the original paper, that will be clearer. But that also means that, if you believe that this blog is a way of making some ideas better known, I will not contribute to popularize nice ideas like those of [1] just because the paper is too well-written. Yet another effect of the old saying: “no good deed goes unpunished“, perhaps. 🙁

Let me try and counter this effect. Maybe I will convince you to look at [1] instead, and then I will have accomplished my goal. Also, while writing this, I realized I ought to talk about a few questions that seemed natural to me but—unless I have overlooked something—are not addressed in [1] or [2]: mostly, the resulting d-sobrification monad and the fact that it is idempotent, just like the good old sobrification monad. As a counterpart, I will abstain from talking about a lot of points addressed in [1] and [2], at least for now.

Stone duality in just a few seconds

Given any topological space X, we can form its lattice OX of open subsets, ordered by inclusion. This is a complete lattice, with a funny property: binary intersections distribute over arbitrary unions. Hence OX is a frame: a complete lattice in which the frame distributivity law u ∧ ⋁_{i ∈ I} v_i = ⋁_{i ∈ I} (u ∧ v_i) holds. (⋁ is supremum, ∧ is infimum; suprema are just unions in OX and finite infima are intersections.)

Conversely, given a frame L, one can retrieve a topological space X≝pt L such that OX looks as close as we can to L. The elements of pt L are the points of L, which are defined as its completely prime filters: a filter of L is an upwards-closed subset x of L that contains the top element of L (equivalent, that is non-empty) and is closed under ∧; it is completely prime if ⋁_{i ∈ I} u_i ∈ x entails that u_i ∈ x for some i ∈ I, whatever the family (u_i)_{i ∈ I} of elements of L we consider. The open subsets of pt L are the sets O_u ≝ {x ∈ pt L | u ∈ x}. If that looks mysterious, note that for every space X, for every x ∈ X, the set N_x of all open neighborhoods of x is a completely prime filter in the frame OX. If X is T₀, then N_x entirely characterizes x: there cannot be two distinct points with different sets of open neighborhoods. For a general T₀ space, there will be other completely prime filters than those of the form N_x, except when X is sober. All this is explained in Chapter 8 of the book. This eventually yields an adjunction O ⊣ pt between the category Top of topological spaces and continuous maps on the one hand, and the opposite (namely, with arrows reversed) category Loc of the category Frm of frames and frame homomorphisms.

Oh, I forgot: a frame homomorphism is a map between frames that preserves all suprema and all finite infima. The function O maps every continuous map f : X → Y to the frame homomorphism Of : OY → OX that sends every open subset V of Y to f^–1(V).

If you have got some time, it is instructive to observe that the points of a frame L are exactly the characteristic functions of frame homomorphisms from L to the two-element lattice {0, 1} (with 0<1).

Bitopological spaces

A bitopological space is just a set with two topologies instead of just one, namely a triple (X, τ⁺, τ_^–) where τ⁺ and τ_^– are two topologies on the set X. That is much more interesting than it may look like at first. We have already seen that kind of object several times on this blog, for example here.

The bitopological spaces form a category biTop, whose morphisms are bicontinuous maps: maps f : (X, τ⁺, τ_^–) → (Y, σ⁺, σ_^–) that are simultaneously continuous from (the topological spaces) (X, τ⁺) to (Y, σ⁺) and from (X, τ_^–) → (Y, σ_^–).

Now how would you design something like a Stone-type duality for biTop? Easy, you might think: given a bitopological space (X, τ⁺, τ_^–), we form two frames, the frame of τ⁺-open sets and the frame of τ_^–-open sets. However, if you take two frames L⁺ and L_^–, how do you recover the set of points of X? There is no reason in general why pt L⁺ and pt L^– would be the same, or would even be simply bijectively related. Something else has to be imposed on the two frames.

Let us imagine we did the obvious thing: we decide that the notion dual to that of bitopological space would be two frames L⁺ and L_^–, plus a bijection (possibly having some extra properties) between pt L⁺ and pt L^–. That is not terribly elegant, since it mentions the spaces of points of L⁺ and L_^–, which we would like to avoid citing. Worse, if you start from a bitopological space (X, τ⁺, τ_^–) and define L⁺ as the frame of τ⁺-open subsets of X and L_^– as the frame of τ_^–-open subsets of X, then there will be no meaningful bijection between pt L⁺ and pt L^– at all, unless X is sober under both τ⁺ and τ_^–.

Example A. Let X be the set N of natural numbers, τ⁺ be the Alexandroff topology of its ordering ≤ (whose non-empty open subsets are the upward closures ↑m, m ∈ N), and τ_^– be the Alexandroff topology of its reverse ordering ≥ (whose non-empty open subsets are the downward closures ↓m, m ∈ N, plus N itself). Defining L⁺ and L_^– as above, pt L⁺ will be the sobrification of (N, τ⁺), which one can equate with N ∪ {ω}, where ω is an extra point above all natural numbers, while pt L^– will be the sobrification of (N, τ_^–), which one can equate with N instead. Hence pt L⁺ and pt L^– are not the same: there is one more point in pt L⁺. Oh, there is a bijection between pt L⁺ and pt L^–, but none that would map every element of N to itself. The next example shows that there are cases where there is no bijection at all.

In Example A, you can verify that the sobrifications are as expected by computing them by hand. Alternatively, we can use Hoffmann’s theorem (Fact 8.2.49 in the book): the sobrification of a space with an Alexandroff topology of some preordering ≤ is its space of ideals, with the Scott topology of inclusion.

Example B. Let X be the set of finite words over the binary alphabet {0, 1} (strings of bits). Let ε denote the empty word, ww’ denote the concatenation of two words w and w’. Let τ⁺ be the Alexandroff topology of the prefix ordering ≤, defined as the smallest such that w ≤ ww’ for all (finite) words w and w’ over {0, 1}. Let τ_^– be the Alexandroff topology of the opposite of ≤ (which we will write as ≥). Defining L⁺ and L_^– as above, pt L⁺ is the sobrification of (X, τ⁺), namely the space of ideals of (X, ≤). You should be able to convince yourselves that this is the dcpo of all finite and infinite words over {0, 1}, ordered by prefix, and with the Scott topology. Now pt L⁺ has the cardinality of the continuum, and is therefore not countable. But pt L^– is just (X, τ_^–), and X is countable. Hence in that case, there is no bijection at all between pt L⁺ and pt L^–.

Consistency and totality

Jung and Moshier’s idea to solve the problem is to equip the two frames L⁺ and L_^– with two relations, consistency and totality. They use a trick to simplify the presentation [1, Proposition 3.1], whereby they replace the two frames L⁺ and L_^– by a single one first, with two distinguished elements tt and ff. Instead, I will use Jakl’s equivalent presentation [2, Definition 2.3.2]. This is a bit heavier, but will require less head-scratching later on, hopefully.

Let us first explain the idea on the two frames of open sets of a bitopological space. Instead of writing (X, τ⁺, τ_^–) for a bitopological space, let me just write X, and let O⁺X be its lattice of τ⁺-open subsets (yes, that is just τ⁺), and let O^–X be its lattice of τ^–-open subsets (yes, that is just τ^–). This is notation that I will keep using from now on. A pair (U⁺, U_^–) in O⁺X × O^–X is:

• consistent if and only if U⁺ and U_^– are disjoint;
• total if and only if U⁺ and U_^– cover the whole of X, namely X = U⁺ ∪ U_^–.

Writing con for the consistency relation, namely for the collection of pairs (U⁺, U_^–) that are consistent, and tot for the totality relation, defined similarly, we will see that con and tot must satisfy some remarkable properties. In order to state them, let us observe that O⁺X × O^–X has two natural orderings:

• the information ordering ⊑: (U⁺, U_^–) ⊑ (V⁺, V_^–) if and only if U⁺ ⊆ V⁺ and U^– ⊆ V^–;
• the logical ordering ⊴: (U⁺, U_^–) ⊴ (V⁺, V_^–) if and only if U⁺ ⊆ V⁺ and U^– ⊇ V^–
  (note the reversal in the inclusion between U^– and V^–).

I will not explain why they are called “information” or “logical” (sorry). But the following picture should help visualize the situation.

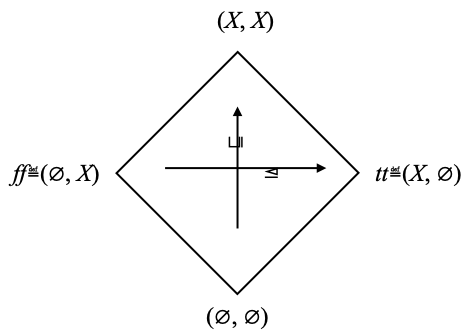
We picture the information ordering ⊑ as going up, while the logical ordering ⊴ goes right. There is a top element (X, X) and a bottom element (∅, ∅) in the information ordering ⊑, and there is a top element tt ≝ (X, ∅) (“true”) and a bottom element ff ≝ (∅, X) (“false”) in the logical ordering ⊴.

Both ⊑ and ⊴ turn O⁺X × O^–X into bounded lattices. Infimum ⊓ with respect to ⊑ is obtained componentwise: (U⁺, U_^–) ⊓ (V⁺, V_^–) = (U⁺ ⋂ V⁺, U_^– ⋂ V^–), and similarly supremum ⊔ with respect to ⊑ is obtained componentwise: (U⁺, U_^–) ⊔ (V⁺, V_^–) = (U⁺ ∪ V⁺, U_^– ∪ V^–).   Infimum ⊼ with respect to ⊴ is given by (U⁺, U_^–) ⊼ (V⁺, V_^–) = (U⁺ ⋂ V⁺, U_^– ∪ V^–) (notice the intersection and the union), and supremum by (U⁺, U_^–) ⊻ (V⁺, V_^–) = (U⁺ ∪ V⁺, U_^– ⋂ V^–).

Now tot and con can be pictured as follows:

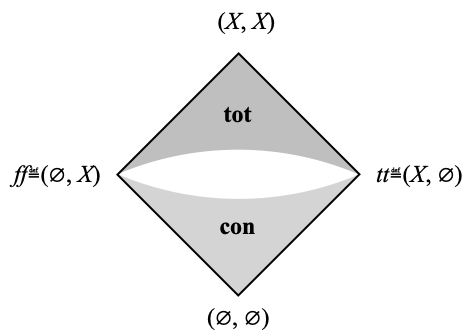
The picture is meant to convey at least some of the properties of tot and con, which we list below:

• tot is upwards-closed in ⊑: if X = U⁺ ∪ U_^– and (U⁺, U_^–) ⊑ (V⁺, V_^–), then X = V⁺ ∪ V_^–;
• con is Scott-closed in ⊑: it is downwards-closed, namely if V⁺ and V_^– are disjoint and (U⁺, U_^–) ⊑ (V⁺, V_^–) then U⁺ and U_^– are disjoint too; and for every directed family (U⁺_i, U_^–i)_{i ∈ I} where U⁺_i and U_^–i are disjoint for every i ∈ I, ∪_{i ∈ I} U⁺_i is disjoint from ∪_{i ∈ I} U^–_i;
• tot contains tt, ff and is closed under ⊼ and ⊻: for ⊻, this means that if X = U⁺ ∪ U_^– and X = V⁺ ∪ V_^–, then X = (U⁺ ∪ V⁺) ∪ (U_^– ⋂ V_^–), which you should be able to verify easily; the case of ⊼ is symmetric;
• con also contains tt, ff and is closed under ⊼ and ⊻: for ⊻, this means that if U⁺ and U_^– are disjoint and if V⁺ and V_^– are disjoint, then U⁺ ∪ V⁺ and U_^– ⋂ V_^– are disjoint; the case of ⊼ is symmetric;
• (Interaction between tot and con.) If (U⁺, U_^–) ∈ con and (V⁺, V_^–) ∈ tot and if either U⁺=V⁺ or U^–=V^–, then (U⁺, U_^–) ⊑ (V⁺, V_^–). Indeed, let us assume U⁺=V⁺. Then (U⁺, U_^–) ∈ con means that U⁺ and U_^– are disjoint, hence every point x of U_^– must be in the complement of U⁺=V⁺; but X = V⁺ ∪ V_^–, so x must be in V_^–. If intead U^–=V^–, then every point x of U⁺ must be in the complement of U^–=V^–, and since X = V⁺ ∪ V_^–, x must be in V_⁺.

I will never use the latter property (interaction between tot and con) in the remainder of this post. Hence this property can be ignored, and we will get exactly the same results. This property was required by T. Jakl to make sure that being well-inside implies being inside. But I will not talk about the well-inside relation in this post. I will not use any property of tot and con either, or in fact that L⁺ and L_^– are frames. We will only need two complete lattices L⁺ and L_^–, with two relations tot and con. Similarly, the adjunction O ⊣ pt works perfectly well as an adjunction between topological spaces and complete lattices, not frames. The situation is similar here. All those fancy extra conditions of being frames, and so on, are only needed to work on the side of frames (or locales), or here on the side of d-frames, which I will not do, at least for today.

d-frames

Following Jakl [2, Definition 2.3.2], we abstract away from bitopological spaces, and we define the following.

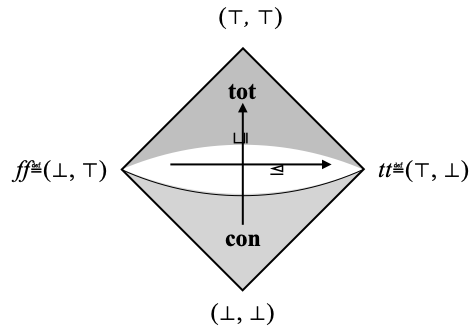
Definition. A d-frame is a quadruple (L⁺, L_^–, tot, con) where:

• L⁺ and L_^– are two frames; we write:
  • ≤ for the ordering on both, ≥ for the reverse ordering on both, ⋀ for infimum on both, ⋁ for supremum on both, ⊤ for the largest element of each, ⊥ for the least element of each;
  • ⊑ for the (information) ordering ≤ × ≤ on L⁺ × L^–,
  • ⊓ for infimum with respect to ⊑: (u⁺, u_^–) ⊓ (v⁺, v_^–) = (u⁺ ⋀ v⁺, u_^– ⋀ v^–),
  • ⊔ for supremum with respect to ⊑: (u⁺, u_^–) ⊔ (v⁺, v_^–) = (u⁺ ⋁ v⁺, u_^– ⋁ v^–),
  • ⊴ for the (logical) ordering ≤ × ≥ on L⁺ × L^–,
  • ⊼ for infimum with respect to ⊴: (u⁺, u_^–) ⊼ (v⁺, v_^–) = (u⁺ ⋀ v⁺, u_^– ⋁ v^–),
  • ⊻ for supremum with respect to ⊴: (u⁺, u_^–) ⊻ (v⁺, v_^–) = (u⁺ ⋁ v⁺, u_^– ⋀ v^–),
  • tt for the largest element (⊤, ⊥) with respect to ⊴,
  • ff for the least element (⊥, ⊤) with respect to ⊴;
• tot is an ⊑-upwards-closed bounded sublattice of (L⁺ × L^–, tt, ff, ⊻, ⊼);
• con is a ⊑-Scott-closed bounded sublattice of (L⁺ × L^–, tt, ff, ⊻, ⊼);
• tot and con satisfaction the interaction law (called (con-tot) by T. Jakl): for all (u⁺, u_^–) ∈ con and (v⁺, v_^–) ∈ tot such that either u⁺=v⁺ or u^–=v^–, (u⁺, u_^–) ⊑ (v⁺, v_^–).

A bounded sublattice of (L⁺ × L^–, tt, ff, ⊻, ⊼) is a subset of L⁺ × L^– that contains tt, ff and is closed under ⊻ and ⊼. We summarize all this in the following picture, which is very similar to what we had earlier. Note that the topmost boundary of con is materialized as a solid line, in order to convey the idea that con is Scott-closed with respect to ⊑, hence contains its upper boundary, made of maximal consistent pairs.

We have defined d-frames in such a way that for every bitopological space X, (O⁺X, O^–X, tot_X, con_X) is a d-frame, where tot_X is the collection of pairs (U⁺, U_^–) ∈ O⁺X × O^–X such that X = U⁺ ∪ U_^– and con_X is the collection of pairs (U⁺, U_^–) ∈ O⁺X × O^–X such that U⁺ and U_^– are disjoint.

Let us write dOX for this d-frame (O⁺X, O^–X, tot_X, con_X).

We can now define a category dFrm whose objects are d-frames, and whose morphisms are the d-frame homomorphisms, defined as follows. A d-frame homomorphism f from a d-frame (L⁺, L_^–, tot, con) to a d-frame (K⁺, K_^–, tot, con) (where we reuse the same notations con and tot for both) is a pair of frame homomorphisms f⁺ : L⁺ → K⁺ and f^– : L^– → K^– that preserve consistency and totality in the sense that:

• for every pair (v⁺, v_^–) ∈ con, (f⁺(v⁺), f^–(v_^–)) ∈ con;
• for every pair (v⁺, v_^–) ∈ tot, (f⁺(v⁺), f^–(v_^–)) ∈ tot.

The identity morphism at (L⁺, L_^–, tot, con) is the pair (id, id) of two identity frame homomorphisms, and composition is obtained by composing the f⁺ and f^– parts separately (i.e., f o g = (f⁺ o g⁺, f^– o g^–)).

Every bicontinuous map f : X → Y between bitopological spaces defines a d-frame homomorphism which we will write as dOf : dOY → dOX, consisting of the pair of frame homomorphisms O⁺f : O⁺Y → O⁺X and O^–f : O^–Y → O^–X, both defined as mapping open sets to their inverse image under f. If (V⁺, V_^–) ∈ con_Y, namely if V⁺ and V_^– are disjoint, then certainly f^–1(V⁺) and f^–1(V_^–) are disjoint, too, showing that dOf preserves consistency. If (V⁺, V_^–) ∈ tot_Y, namely if every point of Y is in V⁺ or in V_^–, then every point of X is in f^–1(V⁺) or in f^–1(V_^–), showing that dOf preserves totality.

The adjunction

The way the classic adjunction O ⊣ pt is built is by defining pt L, for every frame L, as its set of points, alternatively its completely prime filters. Near the beginning of this post, I had mentioned the idea that the points of L are exactly the characteristic functions of frame homomorphisms from L to the two-element lattice {0, 1} (with 0<1). Now that two-element lattice is no random frame: it is O1, where 1 is the (or any) one-element space {*}. Indeed, 1 has exactly two open sets (whatever the topology you put on it—you can only put one anyway), which are ∅ and 1, with ∅ ⊆ 1. This is order-isomorphic to {0, 1} with 0<1. And the space 1 is not random either: it is the terminal object in the category Top.

The idea is that, if you start from a topological space X, its points can be equated with the collection of morphisms from 1 to X. Then O will map each one to a frame homomorphism from OX to O1, and therefore we make the bet that the points of a general frame L, which ought to be the elements of pt L, should be equated with the frame homomorphisms from L to O1.

We proceed similarly with bitopological spaces and frames. The category biTop has a terminal object, which I will continue to write as 1: it consists of just one point *, and its two topologies O⁺1 and O^–1 are equal to the unique topology on 1. The consistent pairs are (∅, 1), (1, ∅) and (∅, ∅). The total pairs are (∅, 1), (1, ∅) and (1, 1). Here is the (4 element) d-frame dO1, graphically. This is a well-known lattice called Four, and which is the collection of truth values in Belnap-Dunn logic (see [2, Section 6]).

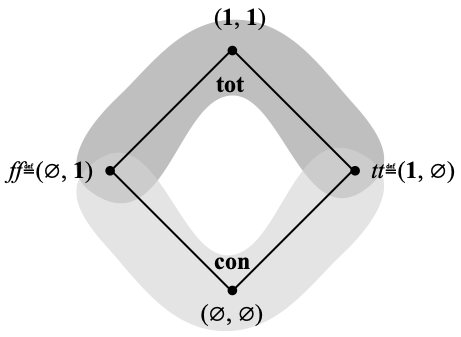
Hence we may define the points of a d-frame (L⁺, L_^–, tot, con) as a d-frame homomorphism from (L⁺, L_^–, tot, con) to Four. In order to make a parallel with the usual adjunction O ⊣ pt, we translate that into the language of completely prime filters. A d-frame homomorphism from (L⁺, L_^–, tot, con) to Four is a pair of frame homomorphisms f⁺ : L⁺ → {∅, 1} and f^– : L^– → {∅, 1} such that:

• (consistency preservation) for all (v⁺, v_^–) ∈ con, (f⁺(v⁺), f^–(v_^–)) is among the consistent pairs (∅, ∅), (∅, 1) or (1, ∅) of Four (namely, is different from (1, 1)), and
• (totality preservation) for all (v⁺, v_^–) ∈ tot, (f⁺(v⁺), f^–(v_^–)) is among the total pairs (1, 1), (∅, 1) or (1, ∅) of Four (namely, is different from (∅, ∅)).

Then f⁺ is the characteristic function of a completely prime filter x⁺ ≝ (f⁺)^–1({1}) and f^– is the characteristic function of a completely prime filter x^– ≝ (f^–)^–1({1}). The consistency preservation condition then reads: for every pair (v⁺, v_^–) ∈ con, it cannot be that v⁺ ∈ x⁺ and v_^– ∈ x^– at the same time; in other words, x⁺ × x^– must be disjoint from con, or in yet another equivalent form every pair (v⁺, v_^–) ∈ con must be such that v⁺ ∉ x⁺ or v_^– ∉ x^–. The totality preservation condition reads: for all (v⁺, v_^–) ∈ tot, it cannot be that v⁺ ∉ x⁺ and v_^– ∉ x^– at the same time; in other words, v⁺ ∈ x⁺ or v_^– ∈ x^–.

Definition [2, Section 2.3.3.1]. A point of a d-frame L ≝ (L⁺, L_^–, tot, con) is a pair (x⁺, x^–) of a point (a completely prime filter) of L⁺ and a point of L_^– such that:

• every pair (u⁺, u_^–) ∈ con is such that u⁺ ∉ x⁺ or u_^– ∉ x^–;
• every pair (u⁺, u_^–) ∈ tot is such that u⁺ ∈ x⁺ or u_^– ∈ x^–.

We write dpt L for the set of points of a d-frame L, with the following two topologies:

• O⁺dpt L consists of the sets O⁺_u⁺ ≝ {(x⁺, x^–) ∈ dpt L | u⁺ ∈ x⁺}, where u⁺ ranges over L⁺;
• O^–dpt L consists of the sets O^–_{u^_} ≝ {(x⁺, x^–) ∈ dpt L | u^– ∈ x^–}, where u^– ranges over L^–.

It is clear that dpt L is a bitopological space, for every d-frame L.

The adjunction O ⊣ pt has a unit, which maps every point x of any topological space X to the completely prime filter {U ∈ OX | x ∈ U}—a point of pt OX. Similarly, given a bitopological space X, we can form its d-frame dOX, and then the bitopological space dpt dOX, and build the following bicontinuous map.

Proposition A. For every bitopological space X, there is a bicontinuous map η_X : X → dpt dOX defined by η_X(x) ≝ (η⁺_X(x), η^–_X(x)) where η⁺_X(x) ≝ {U⁺ ∈ O⁺X | x ∈ U⁺} and η^–_X(x) ≝ {U^– ∈ O^–X | x ∈ U^–}).

Proof. We must first show that η_X(x), as it is defined, is a point of the d-frame dOX. Just like with the O ⊣ pt adjunction, η⁺_X(x) and η^–_X(x) are completely prime filters of O⁺X and of O^–X respectively. For every consistent pair (U⁺, U^_–) in O⁺X × O^–X, namely such that U⁺ and U^_– are disjoint, we must have that U⁺ is not in η⁺_X(x) or that U^– is not in η^–_X(x): otherwise, by definition, x would be in U⁺ and in U^–, contradicting the fact that U⁺ and U^_– are disjoint. For every total pair (U⁺, U^_–) in O⁺X × O^–X, namely such that X = U⁺ ∪ U^_–, we must have that U⁺ is in η⁺_X(x) or that U^– is in η^–_X(x): otherwise, by definition, x would be not be in U⁺ and not be in U^– either, contradicting the fact that U⁺ and U^_– together cover the whole of X.

Next, we must show that η_X is bicontinuous, namely that η_X is continuous from X with the O⁺X topology to dpt dOX with the O⁺dpt dOX topology, and similarly with minus signs. And indeed, for every U⁺ ∈ O⁺X, the inverse image of O⁺_U⁺ by η_X is the collection of points x ∈ X such that η_X(x) ≝ (η⁺_X(x), η^–_X(x)) is in O⁺_U⁺ = {(x⁺, x^–) ∈ dpt L | U⁺ ∈ x⁺}, namely such that U⁺ ∈ η⁺_X(x), equivalently such that x ∈ U⁺; so that is the set U⁺. We reason similarly with minus signs. ☐

dO defines a functor from biTop to the opposite category dFrm^op. We have already seen its action on objects: for every bitopological space X, dOX is the d-frame (O⁺X, O^–X, tot_X, con_X). Its action on morphisms is obtain by inverse images, just like with the O ⊣ pt adjunction: for every bicontinuous map f : X → Y, dOf : dOY → dOX is the d-frame homomorphism consisting of O⁺f : O⁺Y → O⁺X and O^–f : O^–Y → O^–X, both defined as U ↦ f^–1 (U).

We also have a functor dpt from dFrm^op to biTop. For this one, too, we have seen its action on objects: for every d-frame L, dpt L is the bitopological space described in the latest definition. On morphisms, given any d-frame homomorphism φ : L → K, where L ≝ (L⁺, L_^–, tot, con) and K ≝ (K⁺, K_^–, tot, con) (yes, we write tot and con for both, in order not to make the notation too heavy) consisting of frame homomorphisms φ⁺ : L⁺ → K⁺ and φ^– : L^– → K^– that preserve consistency and totality, we define dpt φ : dpt K → dpt L as mapping every point (x⁺, x^–) of K to ((φ⁺)^–1 (x⁺), (φ^–)^–1 (x^–)).

Proposition B. dpt is a functor from dFrm^op to biTop.

Proof. Using the notation above, we first verify that dpt φ maps points (x⁺, x^–) of K of points of L. The sets (φ⁺)^–1 (x⁺) and (φ^–)^–1 (x^–) are completely prime filters, and this is verified as (or follows from) the fact that pt maps morphisms in Frm^op to morphisms in Top. I will let you do the exercise, if you doubt it.

For every consistent pair (v⁺, v_^–) in L⁺ × L^–, we must show that v⁺ ∉ (φ⁺)^–1 (x⁺) or v_^– ∉ (φ^–)^–1 (x^–), namely that φ⁺(v⁺) ∉ x⁺ or φ^–(v^–) ∉ x^–. Since φ preserves consistency, the pair (φ⁺(v⁺), φ^–(v^–)) is consistent, and the result then follows from the fact that (x⁺, x^–) is a point, more particularly that every consistent pair has its first component outside x⁺ or its second component outside x^–.

For every total pair (v⁺, v_^–) in L⁺ × L^–, we must show that v⁺ ∈ (φ⁺)^–1 (x⁺) or v_^– ∈ (φ^–)^–1 (x^–), namely that φ⁺(v⁺) ∈ x⁺ or φ^–(v^–) ∈ x^–. The argument is entirely similar. Since φ preserves totality, the pair (φ⁺(v⁺), φ^–(v^–)) is total, and the result then follows from the fact that (x⁺, x^–) is a point, more particularly that every total pair has its first component inside x⁺ or its second component inside x^–.

Next, we need to show that dpt φ is bicontinuous. For every v⁺ ∈ L⁺, the inverse image of O⁺_v⁺ = {(y⁺, y^–) ∈ dpt L | v⁺ ∈ y⁺} by dpt φ is the collection of points (x⁺, x^–) of K such that v⁺ ∈ (φ⁺)^–1 (x⁺), namely such that φ⁺ (v⁺) ∈ x⁺; that is O⁺_{φ⁺ (v⁺)}. Similarly with minus signs.

Finally, the fact that dpt maps identity morphisms to identity maps and preserves composition is easy. ☐

The following says that dO is left adjoint to dpt. We use the characterization of adjunctions F ⊣ U of Diagram (5.2), Section 5.5.1 of the book. Given a functor F : C → D, and an assignment of an object UL for every object L of D, plus a morphism η_X : X → UFX for every object X of C, F is left adjoint to U with unit η if and only if for every morphism f : X → UL in C, there is a unique morphism f^! : FX → L in D such that Uf^! o η_X = f. The following is the case where C=biTop, D=dFrm^op, F=dO, U=dpt, and η_X was given in Proposition A. One should pay attention that morphisms f^! : FX → L in D are morphisms f^! : dOX → L in dFrm^op, namely d-frame homomorphisms f^! : L → dOX—in other words, be careful about arrow reversals.

Theorem C. For every bitopological space X, for every d-frame L ≝ (L⁺, L_^–, tot, con), for every bicontinuous map f : X → dpt L, there is a unique d-frame homomorphism f^! : L → dOX such that dpt f^! o η_X = f. Hence there is an adjunction dO ⊣ dpt between biTop and dFrm^op, with unit η as defined in Proposition A.

Proof. For every x ∈ X, f (x) is a point of L, which is a pair that we will write as (f⁺ (x), f^– (x)); f⁺ (x) is a point (a completely prime filter) of L⁺, and f^– (x) is a point (a completely prime filter) of L^–.

The proof proceeds almost exactly as with O ⊣ pt (see Theorem 8.1.26 in the book). If f^! exists, and writing it as the pair of two frame homomorphisms f^!+ and f^!–, then for every x ∈ X, f (x) must be equal to dpt f^! (η_X (x)) = ((f^!+)^–1 (η⁺_X(x)), (f^!–)^–1 (η^–_X(x))) = ({v⁺ ∈ L⁺ | x ∈ f^!+ (v⁺)}, {v^– ∈ L^– | x ∈ f^!– (v^–)}). Looking at the first components, f⁺ (x) = {v⁺ ∈ L⁺ | x ∈ f^!+ (v⁺)} for every x ∈ X; so, for every x ∈ X, for every v⁺ ∈ L⁺, v⁺ ∈ f⁺ (x) if and only if x ∈ f^!+ (v⁺); therefore, for every v⁺ ∈ L⁺, f^!+ (v⁺) must be equal to {x ∈ X | v⁺ ∈ f⁺ (x)}. Similarly, for every v^– ∈ L^–, f^!– (v^–) must be equal to {x ∈ X | v^– ∈ f^– (x)}. This shows that f^!+ and f^!– are determined uniquely, hence also f^!.

We now define f^!+ (v⁺) as {x ∈ X | v⁺ ∈ f⁺ (x)} for every v⁺ ∈ L⁺ and f^!– (v^–) as {x ∈ X | v^– ∈ f^– (x)} for every v^– ∈ L^–. Since v⁺ ∈ f⁺ (x) if and only if f (x) ∈ O⁺_v⁺ if and only if x ∈ f^–1 (O⁺_v⁺), and since f is bicontinuous, f^!+ (v⁺) = f^–1 (O⁺_v⁺) is in O⁺X; similarly, f^!– (v^–) = f^–1 (O^–_v^–) is in O^–X. Let us verify that the two maps f^!+ and f^!– are frame homomorphisms. We deal with the case of f^!+ only; let us recall that O⁺_v⁺ ≝ {(y⁺, y^–) ∈ dpt L | v⁺ ∈ y⁺}:

• If v⁺ = ⊤, then O⁺_v⁺ = {(y⁺, y^–) ∈ dpt L | ⊤ ∈ y⁺} is the whole of dpt L, since ⊤ belongs to every completely prime filter y⁺; then f^!+ (v⁺) = f^–1 (dpt L) is the whole of X, which is the top element of O⁺X.
• Binary infima. For all v⁺, v’⁺ ∈ L⁺, the elements of O⁺_v⁺ ⋂ O⁺_v’⁺ are the points (y⁺, y^–) of L such that both v⁺ and v’⁺ are in y⁺; since y⁺ is a filter, that is equivalent to the fact that v⁺ ⋀ v’⁺ is in y⁺. In other words, the elements of O⁺_v⁺ ⋂ O⁺_v’⁺ are the same as those of O⁺_{v⁺ ⋀ v’⁺}. Then f^!+ (v⁺ ⋀ v’⁺) = f^–1 (O⁺_{v⁺ ⋀ v’⁺}) = f^–1 (O⁺_v⁺ ⋂ O⁺_v’⁺) = f^–1 (O⁺_v⁺) ⋂ f^–1 (O⁺_v’⁺) is the infimum of f^!+ (v⁺) and of f^!+ (v’⁺).
• Arbitrary suprema. Let (v_i⁺)_{i ∈ I} be an arbitrary family in L⁺, with supremum v⁺. The elements of O⁺_v⁺ are the points (y⁺, y^–) of L such that v⁺ ∈ y⁺. If so, then some v_i⁺ is in y⁺, because y⁺ is completely prime; conversely, if some v_i⁺ is in y⁺, then v⁺ is, too, since y⁺ is upwards-closed. Hence the elements of O⁺_v⁺ are the points (y⁺, y^–) of L such that v_i⁺ is in y⁺ for some i ∈ I. In other words, O⁺_v⁺ = ∪_{i ∈ I} O⁺_vi⁺. Then f^!+ (v⁺) = f^–1 (O⁺_v⁺) = f^–1 (∪_{i ∈ I} O⁺_vi⁺) = ∪_{i ∈ I} f^–1 (O⁺_vi⁺) = ∪_{i ∈ I} f^!+ (v_i⁺), showing that f^!+ preserves suprema.

We can now define f^! as the pair of frame homomorphisms f^!+ and f^!–. Let us check that f^! preserves consistency and totality. For every consistent pair (v⁺, v^–) in L⁺ × L^–, we need to show that (f^!+ (v⁺), f^!– (v^–)) is consistent, namely that f^!+ (v⁺) and f^!– (v^–) are disjoint. A point in their intersection would be a point x in X such that v⁺ ∈ f⁺ (x) and v^– ∈ f^– (x). But f (x) = (f⁺ (x), f^– (x)) is a point of L, and since (v⁺, v^–) is consistent, v⁺ ∉ f⁺ (x) or v^– ∉ f^– (x) (see the condition on consistency for points of a d-frame), so there is indeed no point in the intersection of f^!+ (v⁺) and f^!– (v^–), and hence (f^!+ (v⁺), f^!– (v^–)) is consistent. For every total pair (v⁺, v^–) in L⁺ × L^–, we claim that (f^!+ (v⁺), f^!– (v^–)) is consistent, namely that every point x of X must be in f^!+ (v⁺) or in f^!– (v^–). By the condition on totality for points of a d-frame, since (v⁺, v^–) is total and f (x) = (f⁺ (x), f^– (x)) is a point of L, v⁺ ∈ f⁺ (x) or v^– ∈ f^– (x); in the first case x is in f^!+ (v⁺), and in the second case x is in f^!– (v^–). This all finishes to show that f^! preserves consistency and totality, hence that f^! is a d-frame homomorphism.

Finally, for every x ∈ X, dpt f^! (η_X (x)) = ((f^!+)^–1 (η⁺_X(x)), (f^!–)^–1 (η^–_X(x))) = ({v⁺ ∈ L⁺ | x ∈ f^!+ (v⁺)}, {v^– ∈ L^– | x ∈ f^!– (v^–)}) (by definition of η_X) = ({v⁺ ∈ L⁺ | v⁺ ∈ f⁺ (x)}, {v^– ∈ L^– | v^– ∈ f^– (x)}) (by definition of f^!) = (f⁺ (x), f^– (x)) = f (x). ☐

D-sobrification

Up to natural isomorphism, the sobrification of a topological space X is pt OX. Its elements are the completely prime filters F of open subsets of X. For each such F, the union U₀ of all the open subsets U that are not in F is itself open and not in F, because F is completely prime. Hence U₀ is the largest open subset of X that is not in F, and therefore the open subsets of X that are in F are exactly those that are not included in U₀. Writing C for the complement of U₀, C is a closed subset of X, and the open subsets that are in F are exactly those that intersects C.

Additionally, C is irreducible: it is non-empty (otherwise no open set would intersect C, showing that no open set would be in F, which is impossible for a filter), and if C intersects any two open sets U and V, then it intersects U ⋂ V (since C intersects U, U is in F and similarly V is in F; since F is a filter, U ⋂ V is in F, hence intersects C).

One can show that, conversely, every irreducible closed subset C of X gives rise to a completely prime filter of open subsets of X, obtained as the collection of open subsets of X that intersect C. This gives rise to an isomorphic representation of the sobrification of X as the space SX of irreducible closed subsets of X. Transporting over the topology of pt OX, whose open sets are the sets O_U ≝ {F ∈ pt OX | U ∈ F}, where U ranges over OX, we obtain a topology whose open sets are ♢U ≝ {C ∈ SX | U intersects C}.

Let us play a similar game with bitopological spaces and d-frames. The d-sobrification of a bitopological space X is dpt dOX, and we will look for a similar, more convenient representation that will be naturally isomorphic to it. The points of dpt dOX are the pairs (F⁺, F^–) where:

• F⁺ is a completely prime filter of elements of O⁺X,
• F^– is a completely prime filter of elements of O^–X,
• for every consistent pair (U⁺, U^–) in O⁺X × O^–X (namely, U⁺ and U^– are disjoint), U⁺ is not in F⁺ or U^– is not in F^–,
• for every total pair (U⁺, U^–) in O⁺X × O^–X (namely, the union of U⁺ and of U^– is the whole of X), U⁺ is in F⁺ or U^– is in F^–.

As above, we replace F⁺ by the O⁺X-closed subset C⁺ of X that is the complement of the largest element of O⁺X that is not in F⁺, and similarly we replace F^– by C^–. Hence C⁺ is an element of the space we will write as S⁺X, which is the sobrification of X in its O⁺X topology, and C^– is an element of the space we will write as S^–X, which is the sobrification of X in its O^–X topology.

The consistency condition then reads: for every pair of disjoint sets U⁺ ∈ O⁺X and U^– ∈ O^–X, U⁺ is disjoint from C⁺ or U^– is disjoint from C^–. Taking the contrapositive: for every pair of sets U⁺ ∈ O⁺X and U^– ∈ O^–X such that U⁺ intersects C⁺ and U^– intersects C^–, it must be the case that U⁺ and U^– intersect.

The totality condition reads: for every pair of sets U⁺ ∈ O⁺X and U^– ∈ O^–X whose union is the whole of X, U⁺ must intersect C⁺ or U^– must intersect C^–. I claim that this condition simplifies to the fact that C⁺ and C^– intersect. Indeed, if the condition holds, then take U⁺ to be the complement of C⁺ and U^– to be the complement of C^–. Then U⁺ does not intersect C⁺ and U^– does not intersect C^–, so the contrapositive of the condition entails that U⁺ ∪ U^– cannot be equal to X; hence that C⁺ ⋂ C^– cannot be empty. Conversely, if C⁺ ⋂ C^– is non-empty, and if U⁺ ∪ U^– = X, then (U⁺ ∪ U^–) ⋂ C⁺ ⋂ C^– is non-empty, so (U⁺ ⋂ C⁺ ⋂ C^–) ∪ (U^– ⋂ C⁺ ⋂ C^–) is non-empty, and that implies that U⁺ intersects C⁺ ⋂ C^– (hence C⁺) or that U^– intersects C⁺ ⋂ C^– (hence C^–).

This leads us to the following definition. Let me remind you that for a bitopological space X, S⁺X denotes its sobrification with respect to its O⁺X-topology (the collection of O⁺X-irreducible closed subsets of X), while S^–X denotes its sobrification with respect to its O^–X-topology (the collection of O^–X-irreducible closed subsets of X).

Definition (d-sobrification). The d-sobrification of a bitopological space X is the bitopological space dSX:

• whose set of points is the collection of pairs (C⁺, C^–) ∈ S⁺X × S^–X such that:
  • (a) C⁺ and C^– intersect,
  • (b) and for every pair of sets U⁺ ∈ O⁺X and U^– ∈ O^–X, if U⁺ intersects C⁺ and U^– intersects C^–, then U⁺ and U^– intersect;
• whose first topology O⁺ dSX consists of those sets of the form ♢⁺U⁺ ≝ {(C⁺, C^–) ∈ dSX | U⁺ intersects C⁺}, where U⁺ ranges over O⁺X;
• whose second topology O^– dSX consists of those sets of the form ♢^–U^– ≝ {(C⁺, C^–) ∈ dSX | U^– intersects C^–}, where U^– ranges over O^–X.

I will leave the following without proof, but I hope you should be convinced: dSX is isomorphic (in biTop) to dpt dOX. In fact, dS is, up to natural isomorphism, the monad associated with the adjunction dO ⊣ dpt.

Composing the unit η_X of the adjunction dO ⊣ dpt with that isomorphism, we obtain a map, which I will continue to write as η_X (hopefully this won’t lead to too much confusion), but from X to dSX, and which is the unit of the monad dS on biTop; for every x ∈ X,

η_X (x) = (↓⁺x, ↓^–x),

where ↓⁺ is downward closure with respect to the specialization preordering ≤⁺ of O⁺X and ↓^– is downward closure with respect to the specialization preordering ≤^– of O^–X.

(Let us check it: the image of x should be (C⁺, C^–), where C⁺ is the complement of the largest set in the complement of η⁺_X(x) ≝ {U⁺ ∈ O⁺X | x ∈ U⁺}, and similarly with C^–. Hence C⁺ is the smallest O⁺X-closed set that contains x, namely its closure, which happens to be its downward closure in the associated specialization preordering ≤⁺. We reason similarly with minus signs.)

Lemma 8.2.26 of the book states that, in the context of topological spaces, the lattice OSX of open subsets of the sobrification SX of a space X is order-isomorphic to OX. We have a similar situation here.

Proposition E. For every bitopological space X, the map ♢⁺ is an order-isomorphism of O⁺X onto O⁺ dSX, and the map ♢^– is an order-isomorphism of O^–X onto O^– dSX.

Proof. We only deal with ♢⁺, since the case of ♢^– is similar. ♢⁺ is surjective by definition of O⁺ dSX. If U⁺ ⊆ V⁺, then every point (C⁺, C^–) ∈ dSX such that U⁺ intersects C⁺ is also such that V⁺ intersects C⁺, so ♢⁺ is monotonic. It remains to show that ♢⁺ is order-reflecting, namely that ♢⁺U⁺ ⊆ ♢⁺V⁺ implies U⁺ ⊆ V⁺, where U⁺ and V⁺ are arbitrary elements of O⁺X.

Since ♢⁺U⁺ ⊆ ♢⁺V⁺, every point (C⁺, C^–) ∈ dSX such that U⁺ intersects C⁺ is also such that V⁺ intersects C⁺. Let x be any point in U⁺. Then let (C⁺, C^–) ≝ η_X (x) = (↓⁺x, ↓^–x). U⁺ intersects C⁺ (at x), so by assumption V⁺ intersects C⁺ = ↓⁺x. Since V⁺ is upwards-closed with respect to ≤⁺, x must be in V⁺. Since x is arbitrary in U⁺, U⁺ ⊆ V⁺. ☐

Lemma F. For every bitopological space X, for every U⁺ ∈ O⁺X, (η_X)^–1 (♢⁺U⁺) = U⁺; for every U^– ∈ O^–X, (η_X)^–1 (♢^–U^–) = U^–.

Proof. (η_X)^–1 (♢⁺U⁺) is the collection of points x of X such that ↓⁺x intersects U⁺. Since U⁺ is upwards-closed with respect to ≤⁺, the latter condition is equivalent to: x ∈ U⁺. Hence (η_X)^–1 (♢⁺U⁺) = U⁺. We reason similarly in order to show that (η_X)^–1 (♢^–U^–) = U^–. ☐

Fact 8.2.24 of the book states that, relative to the O ⊣ pt adjunction, the unit at a space X is bijective if and only if it is a homeomorphism, and that this is equivalent to X being sober. We have a similar phenomenon here, and we use the resulting condition as a definition of the analogous notion of d-sobriety.

Proposition G. For a bitopological space X, the following are equivalent:

1. η_X : X → dSX is bijective;
2. η_X : X → dSX is an isomorphism in biTop;
3. X is d-sober, namely every irreducible pair is equal to (↓⁺x, ↓^–x) for a unique point x of X.
   An irreducible pair is a pair (C⁺, C^–) ∈ S⁺X × S^–X (namely, of irreducible closed subsets of X with its first and second topologies respectively) such that:
   • (a) C⁺ and C^– intersect,
   • (b) and for every pair of sets U⁺ ∈ O⁺X and U^– ∈ O^–X, if U⁺ intersects C⁺ and U^– intersects C^–, then U⁺ and U^– intersect.

Proof. Condition 3 is simply a rephrasing of condition 1, hence is trivially equivalent to it. Clearly, condition 2 implies condition 1. Let us show that condition 1 implies condition 2. We assume that η_X is bijective. Let g be its inverse. We need to show that g is bicontinuous, namely that g is continuous from dSX with its O⁺ dSX topology to X with its O⁺X topology, and from dSX with its O^– dSX topology to X with its O^–X topology. By Lemma F, for every U⁺ ∈ O⁺X, (η_X)^–1 (♢⁺U⁺) = U⁺; hence g^–1 (U⁺) = ♢⁺U⁺. Similarly, g^–1 (U^–) = ♢^–U^–, proving the claim. ☐

The relation to sobrification

We can always see any topological space X as a bitopological space, in many ways.

One is to define O⁺X as the original topology OX, and to define O^–X as the indiscrete topology, whose only open subsets are ∅ and X. Then S⁺X is the usual sobrification SX of X, and S^–X consists of just one element, which is X itself (if X is non-empty; otherwise, S^–X is empty). If X is empty, then dSX is empty. Otherwise, the points of dSX are the irreducible pairs (C⁺, X) ∈ S⁺X × S^–X, and being an irreducible pair means that: (a) C⁺ intersects X (trivially true) and (b) for every open subset U⁺ ∈ O⁺X = OX that intersects C⁺, for the unique U^– ∈ O^–X that intersects X (namely, X itself), U⁺ intersects U^– (that is trivially true, too). In other words, the points of dSX are the pairs (C, X) where C ∈ SX (if X is non-empty), so we can equate the points of dSX with those of SX.

The first topology O⁺ dSX consists of those sets of the form ♢⁺U ≝ {(C, X) ∈ dSX | U intersects C}, where U ranges over OX, and that topology can therefore be equated with that of SX.

The second topology O^– dSX consists of those sets of the form ♢^–U^– ≝ {(C, X) ∈ dSX | U^– intersects X}, where U^– ranges over {∅, X}. Those are just ∅ and dSX, hence that second topology is just the indiscrete topology.

All this holds provided that X is non-empty. If X is empty, then dSX and SX are both empty. In each case, we have therefore shown:

Fact H. Let Ind : Top → biTop be the functor that maps every topological space X to the bitopological space whose first topology is OX and whose second topology is the indiscrete topology, and which is the identity on morphisms. Then dS o Ind = Ind o S.

As I said above, there are several ways of considering a topological space X as a bitopological space, but the others do not behave as well. I will let you check by yourselves that:

• If you consider a topological space X as a bitopological space by taking OX for its first topology and the discrete topology for its second topology, then dSX will be the collection of irreducible pairs (C, {x}) where C ∈ SX and x ∈ X; irreducible means that: (a) x ∈ C and (b) every open subset U of X that intersects C contains x, namely x is the largest element of C. In other words, dSX is the collection of points (↓x, {x}) with x ∈ X, and one can check that with the appropriate two topologies, dSX is isomorphic to X itself, seen as a bitopological space with its original topology and the discrete topology.
• If you consider a topological space X as a bitopological space by taking OX for both topologies, then dSX is a bit weird. Its points are the irreducible pairs (C⁺, C^–) ∈ SX × SX, and irreducibility means that: (a) C⁺ and C^– intersect and (b) for every pair of sets U⁺, U^– ∈ O^–X, if U⁺ intersects C⁺ and U^– intersects C^–, then U⁺ and U^– intersect. For example, we find all the pairs (↓x⁺, ↓x^–) such that (a) x⁺ and x^– have a common lower bound and (b’) x⁺ and x^– have a common upper bound ((b’) is implied by (b) but is not equivalent to it even when C⁺=↓x⁺ and C^–=↓x^–, unless X is weakly Hausdorff). Let us note that there is no reason why x⁺ and x^– should be the same point. It follows that, even if X is sober (as a topological space), hence SX is isomorphic to X, dSX contains more points than X.

The d-sobrification monad is idempotent

For every topological space X, its sobrification SX is sober (Corollary 8.2.23 in the book). That may seem natural: a sobrification should be sober just like a completion should be complete, and so on. But that is also not completely trivial. This means that SSX is (naturally) homeomorphic to SX, and is indicative that S is an idempotent monad.

An adjunction F ⊣ U such that the unit at every object of the form U(-) is an isomorphism is called an idempotent adjunction. This has many other equivalent definitions. (The one I have taken is item 7 of Definition 1.1 of the nCatLab article. I have already talked about idempotent adjunctions here for example, and I have already mentioned the fact that the monad UF would then be an idempotent monad.) The O ⊣ pt adjunction is idempotent, since the unit at every space of the form pt L (for every frame L) is an isomorphism. Indeed, pt L is sober (see Proposition 8.2.11 in the book).

We have a similar situation here. Strangely, I have not spotted this result in [1] or in [2], but then my reading of those was very cursory. Let us proceed: our goal is to show that dpt L is d-sober for every d-frame L, much as pt L is sober for every frame L. Now sobriety splits into two properties: a topological space is sober if and only if it is T₀ and every irreducible closed subset is the closure of some point. (That point is then unique because of the T₀ property.) Similarly:

Lemma I. A bitopological space X is d-sober if and only if it is:

• pairwise T₀, namely its patch topology, defined as the coarsest topology finer than both O⁺X and O^–X, is T₀; or equivalently, the intersection of the specialization preorderings ≤⁺ and ≤^– of O⁺X and O^–X respectively is a partial ordering (is antisymmetric);
• and every irreducible pair (C⁺, C^–) ∈ S⁺X × S^–X is of the form (↓⁺x, ↓^–x) for some point x of X.

Proof. We first show that all the conditions defining pairwise T₀ spaces are equivalent. It suffices to observe that the specialization preordering ≤ of the patch topology is the intersection of ≤⁺ and ≤^–. Indeed, if x ≤ y then every patch-open set containing x contains y, and this applies notably to all the subsets U ∈ O⁺X that contain x, so x ≤⁺ y. Similarly, x ≤^– y. Conversely, if x ≤⁺ y and x ≤^– y, then for every patch open subset U that contains x, we can write U as a union of intersections U_i⁺ ⋂ U_i^–; one of them contains x, and then y ∈ U_i⁺ since x ≤⁺ y and y ∈ U_i^– since x ≤^– y; therefore y ∈ U.

Let X be d-sober. By definition, every irreducible pair is of the form (↓⁺x, ↓^–x) for some (unique) point x of X. Let ≤ be the intersection of ≤⁺ and ≤^–. We assume that x ≤ y and y ≤ x, and we wish to show that x=y. The pairs (↓⁺x, ↓^–x) and (↓⁺y, ↓^–y) are irreducible, because they are equal to η_X(x) and to η_X(y) respectively, and η_X takes its values in dSX. But ↓⁺x=↓⁺y since x ≤⁺ y and y ≤⁺ x, and similarly ↓^–x=↓^–y. Hence (↓⁺x, ↓^–x) and (↓⁺y, ↓^–y) are equal. Since X is d-sober, they are of the form (↓⁺z, ↓^–z) for some unique z ∈ X; whence x=z=y, and in particular x=y.

Conversely, let X be such that every irreducible pair is of the form (↓⁺x, ↓^–x) for some point x of X. If we can also write it as (↓⁺y, ↓^–y), then ↓⁺x=↓⁺y, so x ≤⁺ y and y ≤⁺ x, and similarly x ≤^– y and y ≤^– x. Therefore x ≤ y and y ≤ x, so x=y by pairwise T₀-ness. This shows that x is unique. ☐

Theorem J. For every d-frame L ≝ (L⁺, L_^–, tot, con), dpt L is d-sober. The dO ⊣ dpt adjunction is idempotent, so the monad dS is idempotent on biTop.

Proof. Let X ≝ dpt L. Its first topology O⁺dpt L consists of the sets O⁺_u⁺ ≝ {(x⁺, x^–) ∈ dpt L | u⁺ ∈ x⁺}, where u⁺ ranges over L⁺. We claim that the specialization preordering ≤⁺ of X with its first topology is given by (x⁺, x^–) ≤⁺ (y⁺, y^–) if and only if x⁺ ⊆ y⁺. Indeed, (x⁺, x^–) ≤⁺ (y⁺, y^–) if and only if for every u⁺ ∈ L⁺, if (x⁺, x^–) ∈ O⁺_u⁺ then (y⁺, y^–) ∈ O⁺_u⁺; but (x⁺, x^–) ∈ O⁺_u⁺ is equivalent to u⁺ ∈ x⁺ and (y⁺, y^–) ∈ O⁺_u⁺ is equivalent to u⁺ ∈ y⁺, so (x⁺, x^–) ≤⁺ (y⁺, y^–) if and only if every u⁺ ∈ L⁺ that is in x⁺ is in y⁺.

Similarly, the specialization preordering ≤^– of X with its second topology if given by (x⁺, x^–) ≤^– (y⁺, y^–) if and only if x^– ⊆ y^–. The intersection of ≤⁺ and ≤^– is then the product ⊆ × ⊆, which is antisymmetric. Hence, referring to Lemma I, X is pairwise T₀.

Using Lemma I, we need to show that every irreducible pair (C⁺, C^–) ∈ S⁺X × S^–X is of the form (↓⁺z, ↓^–z) for some z ∈ X. Since X = dpt L, we will need to build z as a pair (z⁺, z^–) satisfying certain properties. Also, since (C⁺, C^–) is an irreducible pair, we know that: C⁺ is irreducible closed with respect to O⁺dpt L, C^– is irreducible closed with respect to O^–dpt L, (a) C⁺ and C^– intersect and (b) and for every pair of sets U⁺ ∈ O⁺X and U^– ∈ O^–X, if U⁺ intersects C⁺ and U^– intersects C^–, then U⁺ and U^– intersect.

We define z⁺ as the union ∪{x⁺ | (x⁺, x^–) ∈ C⁺}, and similarly z^– as the union ∪{y^– | (y⁺, y^–) ∈ C^–}. We notice that those unions make sense: for each (x⁺, x^–) ∈ C⁺, x⁺ is a subset of L⁺ (in fact a completely prime filter of elements of L⁺), and similarly with minus signs.

Claim J.1. z⁺ is a completely prime filter of elements of L⁺, z^– is a completely prime filter of elements of L^–.

Proof. We only prove the claim about z⁺. The claim about z^– is entirely similar. Since C⁺ is irreducible (and closed, namely an element of S⁺X), it is non-empty, so it contains some point (x⁺, x^–). Since x⁺ is a (completely prime) filter of elements of L⁺, it contains the top element of L⁺. Then x⁺ ⊆ z⁺ by definition of z⁺, so z⁺ also contains the top element of L⁺.

Also, z⁺ is a union of (completely prime) filters x⁺, which are all upwards-closed in L⁺, so z⁺ is also upwards-closed in L⁺.

Showing that z⁺ is closed under binary infima taken in L⁺ is a bit more complicated. Let u⁺, v⁺ be two elements of z⁺. By definition of z⁺, u⁺ ∈ x⁺ for some point (x⁺, x^–) ∈ C⁺, and v⁺ ∈ y⁺ for some point (y⁺, y^–) ∈ C⁺. We rewrite u⁺ ∈ x⁺ as (x⁺, x^–) ∈ O⁺_u⁺. Similarly, v⁺ ∈ y⁺ means that (y⁺, y^–) ∈ O⁺_v⁺. Hence C⁺ intersects both O⁺_u⁺ and O⁺_v⁺. Since C⁺ is irreducible, C⁺ must intersect their intersection O⁺_u⁺ ⋂ O⁺_v⁺. But O⁺_u⁺ ⋂ O⁺_v⁺ = O⁺_{u⁺⋀ v⁺}, where ⋀ denotes binary infimum in L⁺. (We have already proved that while proving Theorem C. But you may decide to see whether you can prove it by yourself, too.) Therefore we can find a point (t⁺, t^–) in the intersection of C⁺ and of O⁺_{u⁺⋀ v⁺}. By definition of O⁺_{u⁺⋀ v⁺}, u⁺⋀ v⁺ is in t⁺, and by definition of z⁺ as the union of all the first component of points of C⁺, t⁺ is included in z⁺; so u⁺⋀ v⁺ is in z⁺, which is what we wanted to prove.

Finally, we show that z⁺ is completely prime. Let (u_i⁺)_{i ∈ I} be an arbitrary family in L⁺, with supremum u⁺ in z⁺. By definition of z⁺, u⁺ must be in x⁺ for some (x⁺, x^–) ∈ C⁺. Since x⁺ is completely prime, some u_i⁺ is in x⁺, hence in the larger set z⁺. (End of Claim J.1. ☐)

Claim J.2. (z⁺, z^–) is in dpt L.

Proof. Claim J.1 says that z⁺ is a point of L⁺ and that z^– is a point of L^–. We need to show that every pair (u⁺, u_^–) ∈ con is such that u⁺ ∉ z⁺ or u_^– ∉ z^–; and that every pair (u⁺, u_^–) ∈ tot is such that u⁺ ∈ z⁺ or u_^– ∈ z^–. This is a bit technical.

For the first one, let (u⁺, u_^–) ∈ con, and let us assume for the sake of contradiction that u⁺ ∈ z⁺ and u_^– ∈ z^–. By definition of z⁺ and of z^–, there is a point (x⁺, x^–) ∈ C⁺ such that u⁺ ∈ x⁺, and there is a point (y⁺, y^–) ∈ C^– such that u^– ∈ z^–. Since u⁺ ∈ x⁺, x⁺ is in O⁺_u⁺, and similarly y^– is in O^–_u^–. It is time to remember that (C⁺, C^–) is an irreducible pair, and in particular condition (b): since O⁺_u⁺ intersects C⁺ (at (x⁺, x^–)) and O^–_u^– intersects C^– (at (y⁺, y^–)), O⁺_u⁺ and O^–_u^– themselves have a non-empty intersection. Let (t⁺, t^–) be a point in that intersection. By definition of O⁺_u⁺ and of O^–_u^–, u⁺ ∈ t⁺ and u^– ∈ t^–. But, since (t⁺, t^–) is a point, namely an element of L, and since (u⁺, u_^–) ∈ con, we must have u⁺ ∉ t⁺ or u_^– ∉ t^–; and that is impossible.

For the second one, let (u⁺, u_^–) ∈ tot. Since (C⁺, C^–) is an irreducible pair, condition (a) of the definition of irreducible pairs tells us that C⁺ and C^– intersects, say at (x⁺, x^–). Since (x⁺, x^–) is in dpt L, and since (u⁺, u_^–) ∈ tot, we must have u⁺ ∈ x⁺ or u_^– ∈ x^–. But x⁺ ⊆ z⁺ by definition of z⁺, so u⁺ ∈ z⁺ in the first case; similarly, u_^– ∈ z^– in the second case. Hence, whatever happens, u⁺ ∈ z⁺ or u_^– ∈ z^–. (End of Claim J.2. ☐)

Claim J.3. (z⁺, z^–) is in C⁺, and in C^–.

Proof. We will only show that (z⁺, z^–) is in C⁺, the case of C^– is symmetric. By Claim J.2, (z⁺, z^–) is in dpt L, so we only have to assume that (z⁺, z^–) is not in C⁺ and aim for a contradiction. Since C⁺ is (irreducible) closed in X with the topology O⁺dpt L, its complement is in O⁺dpt L, hence is of the form O⁺_u⁺ for some u⁺ ∈ L⁺. The fact that (z⁺, z^–) is not in C⁺ means that (z⁺, z^–) is in O⁺_u⁺, namely that u⁺ ∈ z⁺. By definition of z⁺, there is a point (x⁺, x^–) ∈ C⁺ such that u⁺ ∈ x⁺. In particular, (x⁺, x^–) ∈ O⁺_u⁺. But O⁺_u⁺ is the complement of C⁺, and therefore (x⁺, x^–) ∈ O⁺_u⁺ contradicts (x⁺, x^–) ∈ C⁺. (End of Claim J.3. ☐)

We can now conclude and show that (C⁺, C^–) = (↓⁺z, ↓^–z) where z ≝ (z⁺, z^–) (a point in dpt L, by Claim J.2). In order to do so, we show that C⁺ = ↓⁺z; the proof that C^– = ↓^–z is symmetric. By Claim J.3, z = (z⁺, z^–) ∈ C⁺. Since C⁺ is closed with respect to the topology O⁺dpt L, it is downwards-closed in its specialization ordering ≤⁺, so ↓⁺z ⊆ C⁺. Conversely, every point (x⁺, x^–) ∈ C⁺ is such that x⁺ ⊆ z⁺ by definition of z⁺, namely (x⁺, x^–) ≤⁺ (z⁺, z^–). (Remember our characterisation of ≤⁺, at the beginning of this proof, as being inclusion on first components.) Therefore C⁺ ⊆ ↓⁺z, and then C⁺ = ↓⁺z. As I have said above, we show that C^– = ↓^–z in a symmetric way. (End of proof of Theorem J. ☐)

Let us stop here! You might want to learn more: in [1], you will find that several examples, a proof that every order-separated bitopological space is d-sober (an analogue of the fact that Hausdorff spaces are sober), a study of locally compact d-frames and a bitopological version of the Hofmann-Mislove theorem. In [2], you will find… much more than I can say. This is a PhD thesis! Free d-frame constructions, quotients, Vietoris constructions for bitopological spaces and d-frames, an application to the theory of stably compact spaces (T. Jakl once recommended me his approach of the theory of Nachbin pospaces, and I have not yet talked about it here—sorry), and an application to Belnap-Dunn logic, at least.

1. Achim Jung and M. Andrew Moshier. A Hofmann-Mislove theorem for bitopological spaces. Electronic Notes in Theoretical Computer Science 173:159-175, 2007. Available from https://achimjungbham.github.io/pub/papers/HM-journal.pdf
2. Tomáš Jakl. d-Frames as algebraic duals of bitopological spaces, Ph.D. thesis, Charles University and University of Birmingham, 2018.

— Jean Goubault-Larrecq (June 20th, 2025)