Compactly Choquet-complete spaces II: completely Baire spaces

The compactly Choquet-complete spaces were introduced in [1], and we had started to study them last time, where we had shown that the class of compactly Choquet-complete spaces contains the locally compact sober spaces, are closed under taking G_δ subspaces, and therefore also contains the LCS-complete spaces (the G_δ subspaces of locally compact sober spaces). The latter include Matthew de Brecht quasi-Polish spaces [2], and we have seen that the secound-countable compactly Choquet-complete spaces are exactly the quasi-Polish spaces.

Another important property of compactly Choquet-complete spaces is that they are all Baire, but we can say more.

A Baire space is a space in which every every countable intersection of dense open subsets is dense.  You probably know that every compact Hausdorff space and every complete metric space is Baire.  Those results can be generalized: every locally compact sober space is Baire (Proposition 8.3.24 in the book, and originally a result due to Isbell [3]), every Yoneda-completely quasi-metrizable space is Baire in its open ball topology; both results are in fact special cases of the fact that every Choquet-complete space is Baire, and both locally compact sober spaces and Yoneda-completely quasi-metrizable spaces are Choquet-complete (Theorem 7.6.8 the book).

Baire and completely Baire spaces

It was shown in [1] that every compactly Choquet-complete is Baire.  But, as we have just said, every Choquet-complete space is Baire, not just the compactly Choquet-complete or convergence Choquet-complete spaces.

Something that was not stated in [1] is that every compactly Choquet-complete space is completely Baire.  A completely Baire space is a space X whose closed subsets (with the subspace topology) are all Baire.  It turns out that this is a stronger property than just being Baire. The following counterexample was found on the Math StackExchange.

Countexample A. Let Q be the space of rational numbers with its usual metric topology, and let ⊤ be some point outside of Q. We form the union X of Q and {⊤}, with the topology whose open sets are the empty set, plus all the sets U ∪ {⊤}, where U ranges over the open subsets of Q. Its specialization ordering makes all rational numbers incomparable, and places ⊤ above all of them.

• We argue that X is a Baire space. Every dense open subset of X contains ⊤, because the only one that does not contain ⊤ is the empty set, which is of course not dense. Hence every intersection of dense open subsets of X (even uncountable) contains ⊤. But every subset A of X that contains ⊤ is dense: every non-empty open subset of X contains ⊤, hence intersects A.
• Q is a closed subspace of X. This is due to the fact that {⊤} is open.
• Q is not Baire in the subspace topology. The subspace topology is simply the usual metric topology, and it is well-known that Q is not Baire (see Exercise 7.6.10 in the book).

A reminder on compact and convergent Choquet-completeness

The strong Choquet game is played between two players, α and β. Player β starts the game by picking a point x₀ and an open neighborhood V₀ of x₀. Then α replies with an open neighborhood U₀ of x₀ included in V₀; β picks a possibly different point x₁ in U₀, an open neighborhood V₁ of x₁ included in U₀; α replies with an open neighborhood U₁ of x₁ included in V₁; β picks a possibly different point x₂ in U₁, an open neighborhood V₂ of x₂ included in U₁, and so on. See the following picture.

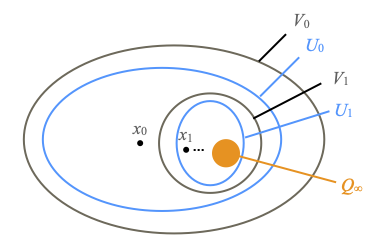
After both players have played for as many turns as there are natural numbers, α is declared to win if ∩_n ∈ N U_n (which is also equal to ∩_n ∈ N V_n) is non-empty. Otherwise, β wins. We say that α wins compactly if and only if ∩_n ∈ N U_n is a non-empty compact set Q_∞ and the sets U_n form a base of open neighborhoods of Q_∞; α wins convergently if and only if it wins compactly and Q_∞ is the upward closure of a point x_∞.

Each player plays according to a strategy: σ for α, τ for β. Player α finds U_n as σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n), and player β finds the pair x_n, V_n as τ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n–1, V_n–1, U_n–1). A strategy σ for α that wins compactly (resp., convergently) against every possible strategy τ that β uses is compactly winning (resp., convergently winning). A space is compactly Choquet-complete (resp., convergence Choquet-complete) if and only if α has a compactly (resp., convergently) winning strategy.

A stationary strategy for α is one that only depends on the last pair x_n, V_n played by β, and we write σ(x_n, V_n) instead of σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) in that case. A space is stationary compactly Choquet-complete (resp., stationary convergence Choquet-complete) if and only if α has a stationary compactly (resp., stationary convergently) winning strategy.

Every compactly Choquet-complete space is completely Baire

Proposition B.  Every closed subspace of a compactly Choquet-complete space is compactly Choquet-complete.  Similarly with stationary compact Choquet-completeness.

Proof. We start with the second part, which is simpler but carries most of the same ideas.  We assume that α has a stationary compactly winning strategy σ on X, and we let F be a closed subset of X, with the subspace topology.

We will use similar game hacking as last time. We define a strategy σ’ for player α on F by letting σ'(x_n, V_n) ≝ σ(x_n, V’_n) where V’_n ≝ V_n ∪ (X–F). In other words, we simulate σ, as though we were playing on X, with the point x_n and some open neighborhood V’_n of x_n in X computed as a function of V_n. We cannot take V_n itself, which is not in general open in X. The V’_n we take is the largest open neighborhood of x_n in X whose intersection with F equals V_n. The following picture may help. In order to play on F, α needs to react to x₀, V₀ (below, left) inside the subspace F, and it uses its strategy σ on x₀, V‘₀, where V‘₀ is shown below, right.

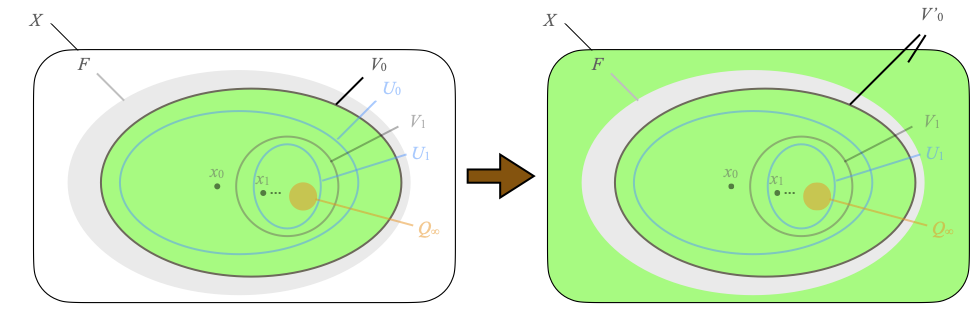
Given any strategy τ for player β on F (not necessarily stationary), we define a new strategy τ’ for player β on X by τ'(x₀, V’₀, U’₀, x₁, V’₁, U’₁, ···, x_n, V’_n, U’_n) ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F, x₁, V’₁ ⋂ F, U’₁ ⋂ F, ···, x_n, V’_n ⋂ F, U’_n ⋂ F). In other words, we let β play in a myopic way, where instead of seeing the open neighborhoods V’_i of x_i in X, it only sees their intersections with the subspace F. This definition is only valid when every point x_i is in F. Otherwise, we define τ'(x₀, V’₀, U’₀, x₁, V’₁, U’₁, ···, x_n, V’_n, U’_n) arbitrarily: we do not care, this case will not happen below.

When α plays according to σ and β plays according to τ’ on X (the σ/τ’ scenario), we obtain:

• x₀, V’₀ where V’₀ ≝ V₀ ∪ (X–F) and x₀, V₀ ≝ τ();
• U’₀ ≝ σ(x₀, V’₀);
• x₁, V’₁ where V’₁ ≝ V₁ ∪ (X–F) and x₁, V₁ ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F) = τ(x₀, V₀, U’₀ ⋂ F);
• U’₁ ≝ σ(x₁, V’₁);
• x₂, V’₂ where V’₂ ≝ V₂ ∪ (X–F) and x₂, V₂ ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F, V’₁ ⋂ F, U’₁ ⋂ F) = τ(x₀, V₀, U’₀ ⋂ F, V₁, U’₁ ⋂ F);
• etc.

When α plays according to σ’ and β plays according to τ on F (the σ’/τ scenario), we obtain:

• x₀, V₀ ≝ τ();
• U₀ ≝ U’₀ ∩ F where U’₀ ≝ σ(x₀, V’₀) (as in the σ/τ’ scenario), V’₀ ≝ V₀ ∪ (X–F);
• x₁, V₁ ≝ τ(x₀, V₀, U₀);
• U₁ ≝ U’₁ ∩ F where U’₁ ≝ σ(x₁, V’₁), and V’₁ ≝ V₁ ∪ (X–F);
• x₂, V₂ ≝ τ(x₀, V₀, U₀, x₁, V₁, U₁);
• etc.

Hence the open sets U_n played by α on F in the σ’/τ scenario are equal to U’_n ∩ F for every n ∈ N, where U’_n is played by α on X in the σ/τ’ scenario.

Since σ is a compactly winning strategy for α on X, the open subsets U’_n played in the σ/τ’ scenario form a base of open neighborhoods of a compact saturated subset Q’_∞ of X.  Let Q_∞ ≝ Q’_∞ ∩ F.  This is the intersection of a compact set with a closed set, hence is compact in X.  Being compact in X and included in F, it is compact in F.  Clearly, Q_∞ is included in every U_n = U’_n ∩ F.  Every open neighborhood of Q_∞ is a set of the form U ∩ F with U open in X (by definition of the subspace topology) that contains Q_∞.  Since Q_∞ = Q’_∞ ∩ F, Q’_∞ is included in Q_∞ ∪ (X–F), which is included in (U ∩ F) ∪ (X–F) = U ∪ (X–F).  But the open subsets U’_n form a base of open neighborhoods of Q’_∞, so one of them is included in U ∪ (X–F).  Then U_n = U’_n ∩ F ⊆ U ∩ F.  This shows that the sets U_n form a base of open neighborhoods of Q_∞ in F.  Therefore σ’ is a compactly winning strategy on F.

We now deal with the first part of the theorem, where the strategies that α uses are no longer assumed to be stationary.  We start with a compactly winning strategy σ on X, which is no longer assumed to be stationary.  We will also build a new strategy σ’, but it will be easier to build it as a memoryful strategy.  The memory will consist of the list of open sets U’₀, U’₁, ···, U’_n–1 played on X until now.

Given a history x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n and a memory U’₀, U’₁, ···, U’_n–1 (for the game played on F), we form the open subsets V’_i ≝ V_i ∪ (X–F) for each i such that 0≤i≤n.  Then we define U’_n ≝ σ(x₀, V’₀, U’₀, x₁, V’₁, U’₁, ···, x_n, V’_n), we add it to the memory—so the new memory is U’₀, U’₁, ···, U’_n–1, U’_n—and we let U_n ≝ U’_n ∩ F be the desired value of σ'(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n).

Whatever strategy τ player β uses to play on F, we show that the sets U_n we obtain by letting α play according to σ’ (as above) and β play according to τ on F are related to the corresponding open subsets U’_n of X obtained by letting α play according to σ and β play according to τ’ on X instead, where τ’ is defined as mapping every history x₀, V’₀, U’₀, x₁, V’₁, U’₁, ···, x_n, V’_n, U’_n to x_n+1, V’_n+1 with x_n+1, V_n+1 ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F, x₁, V’₁ ⋂ F, U’₁ ⋂ F, ···, x_n, V’_n ⋂ F, U’_n ⋂ F) and V’_n+1 ≝ V_n+1 ∪ (X–F); this makes sense if x₀, …, x_n are all in F, otherwise we let x_n+1 ≝ x_n and V_n+1 ≝ U’_n ⋂ F for example (this is an unimportant case, just as in the stationary case we dealt with above).  By related, I mean that U_n = U’_n ∩ F for every n ∈ N.  Let us check this at least on the first few steps on the game, although one should do a proper induction on n ∈ N.

When α plays according to σ and β plays according to τ’ on X (the σ/τ’ scenario), we obtain:

• x₀, V’₀ where V’₀ ≝ V₀ ∪ (X–F) and x₀, V₀ ≝ τ();
• U’₀ ≝ σ(x₀, V’₀);
• x₁, V’₁ where V’₁ ≝ V₁ ∪ (X–F) and x₁, V₁ ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F) = τ(x₀, V₀, U’₀ ⋂ F);
• U’₁ ≝ σ(x₀, V’₀, U’₀, x₁, V’₁);
• x₂, V’₂ where V’₂ ≝ V₂ ∪ (X–F) and x₂, V₂ ≝ τ(x₀, V’₀ ⋂ F, U’₀ ⋂ F, V’₁ ⋂ F, U’₁ ⋂ F) = τ(x₀, V₀, U’₀ ⋂ F, V₁, U’₁ ⋂ F);
• etc.

When α plays according to σ’ and β plays according to τ on F (the σ’/τ scenario), we obtain:

• x₀, V₀ ≝ τ(); those are the same x₀, V₀ as in the σ/τ’ scenario;
• U₀ ≝ U’₀ ∩ F where U’₀ ≝ σ(x₀, V’₀) (as in the σ/τ’ scenario), V’₀ ≝ V₀ ∪ (X–F); the memory was initially empty, and is now equal to the one-element list U’₀; we note that we obtain the same V’₀, and hence also the same U’₀ as in the σ/τ’ scenario;
• x₁, V₁ ≝ τ(x₀, V₀, U₀); those are the same x₁, V₁ as in the σ/τ’ scenario;
• U₁ ≝ U’₁ ∩ F where U’₁ ≝ σ(x₀, V’₀, U’₀, x₁, V’₁), U’₀ ≝ σ(x₀, V’₀) and V’₀ ≝ V₀ ∪ (X–F) as two items above, and V’₁ ≝ V₁ ∪ (X–F); U’₀ and V’₀ are as in the σ/τ’ scenario, so are x₀ and x₁, so is V₁ hence also V’₁, and therefore U’₀ is as in the σ/τ’ scenario, too;
• x₂, V₂ ≝ τ(x₀, V₀, U₀, x₁, V₁, U₁); again, those are the same x₁, V₁ as in the σ/τ’ scenario;
• etc.

Hence U_n = U’_n ∩ F for every n ∈ N.  The rest of the proof is as in the stationary case. Since σ is a compactly winning strategy for α on X, the open subsets U’_n played in the σ/τ’ scenario form a base of open neighborhoods of a compact saturated subset Q’_∞ of X.  We define Q_∞ ≝ Q’_∞ ∩ F, and we verify that the sets U_n form a base of open neighborhoods of Q_∞ in F, because the sets U’_n form a base of open neighborhoods of Q’_∞ in X.  Therefore σ’ is a compactly winning strategy on F.   ☐

Corollary C.  Every compactly Choquet-complete space is completely Baire.

Proof.  Given a compactly Choquet-complete space X and and closed subset F of X, F is compactly Choquet-complete by Proposition B, hence Baire.   ☐

A final word (for now)

A better series of results, compared to what I have explained above, would be to show that:

Conjecture D. Every Π⁰₂ subspace of a compactly Choquet-complete space is compactly-Choquet-complete.

A Π⁰₂ subset of X is a countable intersection of UCO subsets, where a UCO subset (“union of closed and open”) of a topological space is a subset of the form U ⇒ V where U and V are open; the notation U ⇒ V stands for the set of points x such that if x ∈ U then x ∈ V. UCO subsets were mentioned in the March 2019 post on countably presented locales, or in the August 2019 post on sober subspaces and the Skula topology, and the name comes from R. Heckmann. In the February 2021 post, we have shown that every Π⁰₂ subspace of a quasi-Polish space (defined as G_δ subset of an ω-continuous dcpo) is quasi-Polish. Every G_δ subset, every closed subset is a Π⁰₂ subset.

Among the indications that conjecture D might be true, we find:

1. every Π⁰₂ subspace of a completely Baire space is completely Baire [4, Theorem 4.1];
2. every G_δ subspace of a compactly Choquet-complete space is compactly Choquet-complete (Theorem C of last time);
3. every closed subspace of a compactly Choquet-complete space is compactly Choquet-complete (Proposition B in this post).

I have tried to show conjecture D, and there is a strategy that I don’t think is too hard to invent, that makes Q_∞ ≝ ∩_n ∈ N U_n compact and non-empty, but I didn’t manage to show that the open sets U_n form a base of open neighborhoods of Q_∞.

If Conjecture G is true, then one could generalize the proof that every LCS-complete space is compactly Choquet-complete, and show that every Π⁰₂ subspace of a locally compact sober space is compactly Choquet-complete. But I don’t know whether that is true.

1. Matthew de Brecht, Jean Goubault-Larrecq, Xiaodong Jia, and Zhenchao Lyu. Domain-complete and LCS-complete Spaces. In Proceedings of the International Symposium on Domain Theory (ISDT’19), volume 345 of Electronic Notes in Theoretical Computer Science, pages 3–35, Yangzhou, China, June 2019. Elsevier Science Publishers. doi:10.1016/j.entcs.2019.07.014.
2. Matthew de Brecht. Quasi-Polish spaces, Annals of Pure and Applied Logic 164:356–381, 2013.
3. John R. Isbell. Function spaces and adjoints, Mathematica Scandinavica 36:317–339, 1975.
4. Matthew de Brecht.  A generalization of a theorem of Hurewicz for quasi-Polish spaces. Logical Methods in Computer Science, 14(1:13)2018, pages 1–18, 2018; arXiv report 1711.09326.

— Jean Goubault-Larrecq (September 20th, 2025)