Season’s greetings, first!
Last time, I explained how one can build the étale space of a presheaf F over a topological space X. Let me remind you how this is built. I will then show how one can retrieve a sheaf from an étale map, leading to a nice adjunction and its associated monad, sheafification. This is all well-known (see Chapter 10 in [1], for example), but then I would like to apply all that to the presheaf of locally monotone functions of a prestream, which we had already started to examine last time.
From presheaves to étale spaces and maps
Let F be a presheaf over a space X. For each open set U of X, the presheaf gives us a set FU, and restriction maps rUV from FV to FU, for every pair of open sets U ⊆ V. We build the stalk Fx of F at each point, as the quotient F[x]/≡x, where F[x] is the disjoint union of the sets FU, where U ranges over the open neighborhoods of x, and (U, f) ≡x (V, g), if and only if there is an open neighborhood W of x included in both U and V such that rWU(f)=rWV(g). I will often omit the U and V parts, and I will just write f ≡x g instead of (U, f) ≡x (V, g).
The étale space S(X, F) is the disjoint union of all the stalks Fx; its elements are the pairs (x, [f]), where x is a point in X and [f] is the equivalent class modulo ≡x of an element f of a set FU, where U is an open neighborhood of x. There is a projection map p : S(X, F) → X, which maps (x, [f]) to x, and p is a surjective local homeomorphism.
For this to work, we had to define the topology on S(X, F) as the finest that makes all the overlined maps f continuous, where f : U → S(X, F) is defined by f(x) ≝ (x, [f]) for every x in U, this for every open subset U of X and for every f ∈ FU. Finally, we had observed that the sets f(U), where U ranges over the open subsets of X, and f ranges over FU, form a base of the topology of S(X, F).
A surjective local homeomorphism p from a space Y to X is called an étale map on X. As is usual in category theory, the data of a map (or a morphism) includes the specification of the domain and of the codomain. In particular, an étale map on X is given by a pair (Y, p) of a space Y and a surjective local homeomorphism p onto X. We do not need to specify X in the pair, since I said “an étale map on X“, but I may later say “an étale map” to mention a triple (Y, p, X).
From étale maps to sheaves
Let us try to retrieve a presheaf from an étale map (Y, p) on X. We form the sheaf LSect(Y, p) of local sections of p. A local section is a continuous map s from an open subset U of X to Y such that p o s is the identity on U. It is easy to see that LSect(Y, p) is always a sheaf on X—not just a presheaf!—, with the obvious notion of restriction: rVU(s) is really the restriction s|V of s : U → Y to V ⊆ U.
Let us say all that in more categorical terms. For a fixed topological space X, there is a category PreSh(X) of presheaves on X. (Reminder: X is fixed!) Since presheaves on X are just functors from OXop to Set, it should come as no surprise that the morphisms on PreSh(X) are the natural transformations. Explicitly, a morphism φ of presheaves on X from F to G is a collection of functions φU : FU → GU, one for each open subset U of X, which commutes with restrictions.
There is also a full subcategory Sh(X) of sheaves on X. Its objects are the sheaves on X, and its morphisms are the same, namely, natural transformations.
Finally, there is a category Etale(X) of étale maps on X. Its objects are the surjective local homeomorphisms (Y, p) on X, and the morphisms from (Y, p) to (Z, q) are the continuous maps f : Y → Z such that q o f = p. You may have recognized a full subcategory of the slice category Top/X, whose objects are all the pairs (Y, p) where p is a continuous map from Y to X, not just the surjective local homeomorphisms.
There is a functor E : PreSh(X) → Etale(X). On objects, it maps every presheaf F on X to the projection map p : S(X, F) → X, the étale map of F. Its action on morphisms φ : F → G (namely, natural transformations) is defined by E(φ) (x, [f]) ≝ (x, [φ(f)]). I will let you check by yourselves that E(φ) is indeed a continuous map from S(X, F) to S(X, G). This is just a play on symbols; just make sure that you do not get lost in notation.
We have defined the sheaf of local sections LSect(Y, p) of an étale map on X, and this construction, too, extends to a functor from Etale(X) to PreSh(X), and in fact to the full subcategory Sh(X). Given any morphism of étale maps f : LSect(Y, p) → LSect(Z, q), we define LSect(f) ≝ φ as the natural transformation such that, for every subset U of X, for every local section s : U → Y of p, φU(s) is the map f o s, which is a local section (from U to Z) of q.
Those two functors are related, as you may have guessed. For every presheaf F on X, there is a morphism ηF : F → LSect(E(F)) of presheaves on X, which maps every element f of FU to our old friend f : U → S(X, F). Indeed, that is a continuous map, by definition of the topology on S(X, F), and a section of the corresponding étale map p, since f(x)=(x, [f]) for every x in U, by definition. I will let you check that ηF is natural in F, too, although that is really a consequence of the following proposition.
Proposition (E ⊣ LSect). LSect is right adjoint to E, with unit the natural transformation η that we have just defined.
Proof sketch. In order to see this, it is enough to show that, given any morphism φ : F → LSect(Y, p) of presheaves on X, there is a unique morphism φ* : E(F) → (Y, p) of étale maps such that LSect(φ*) o ηF = φ.
If φ* exists, then it must map every element (x, [f]) of S(X, F) to an element y of Y such that p(y)=x, first (being a morphism of étale maps). The condition LSect(φ*) o ηF = φ means that, for every open subset U of X, for every f ∈ FU, φ* o f = φU(f). In other words, for every x ∈ U, we must have φ*(x, [f]) = φU(f). In particular, φ* is unique, if it exists.
Hence we define φ* as mapping (x, [f]), for every open subset U of X and every f ∈ FU, to φU(f)(x). I will let you check the rest for yourselves: that this is well-defined, that this is continuous, and that p(φ*(x, [f])) = x. This is not difficult, just try not to get lost in notation—again. ☐
The counit of the adjunction E ⊣ LSect
The counit ε of the adjunction E ⊣ LSect is defined at each object (Y, p) of Etale(X) by ε(Y, p) ≝ idLSect(Y, p)*, as is usual for every adjunction. Explicitly, ε(Y, p) maps every point (x, [s]) in S(LSect(Y, p)) (where s : U → Y is a local section of p, U is an open neighborhood of x in X, and the equivalence class [s] is taken relative to ≡x) to s(x) ∈ Y. The following is pretty remarkable.
Lemma. The unit ε(Y, p) of the adjunction E ⊣ LSect is a (natural) isomorphism, in Etale(X), from the étale map q : S(LSect(Y, p)) → X that maps (x, [s]) to x, to the étale map p : Y → X.
This may seem extraordinary, since there does not seem to be any way of retrieving (x, [s]) from just one single value s(x) in the range of s, not even considering that s is itself unknown. However, the lemma does not say that ε(Y, p) is an isomorphism of S(LSect(Y, p)) into Y in Top, but an isomorphism in the category Etale(X) of étale maps on X.
Proof. We will build the inverse to ε(Y, p) explicitly. That must be a continuous map ε–1 : Y → S(LSect(Y, p)) such that, for every y in Y, if p(y) is a point x of X, then q(y)=x. In other words, ε–1(y) must be equal to (x, [s]) where x≝p(y), for some local section s : U → Y of p, for some open neighborhood U of x. This is where we need the fact that p is a local homeomorphism. By definition, there is an open neighborhood V of y such that p restricts to a homeomorphism of V onto some open neighborhood U of x. On U, p has exactly one section, and that is s≝p–1|U.
We therefore define ε–1 as mapping every point y of Y to (x, [p–1|U]), where x≝p(y), V is a small enough neighborhood of y, U is the image of V by p—by small enough, we mean that V is small enough around x so that p restricts to a homeomorphism of V onto its image U.
For every point (x, [s]) in S(LSect(Y, p)), we have ε–1(ε(Y, p)(x, [s])) = ε–1(x) = (x, [p–1|U]). We claim that this is equal to (x, [s]). It suffices to show that s and p–1|U agree on a sufficiently small open neighborhood of x. Since s is a local section of p, s is a continuous map from some open neighborhood U’ of x such that p o s = id. The sufficiently small open neighborhood of x is U ∩ U’: for every x’ in U ∩ U’, p(s(x’))=x’, so s(x’)=p–1|U(x’). All this shows that ε–1 o ε(Y, p) = id.
For every point y in Y, we have ε(Y, p)(ε–1(y)) = ε(Y, p)(x, [p–1|U]), where x≝p(y), V is a small enough neighborhood of y, and U is the image of V by p. Hence ε(Y, p)(ε–1(y)) = p–1|U(x) = y. This shows that ε(Y, p) o ε–1 = id.
Finally, we claim that ε–1 is continuous. For this, we do not need to know the definition of ε–1; it suffices to remember that q o ε–1 = p, which follows from the fact that q = p o ε. We take an arbitrary open neighborhood W of ε–1(y) in S(LSect(Y, p)), and we claim that there is an open neighborhood V of y whose image by ε–1 is included in W. Because q is a local homeomorphism, we may replace W by a smaller open neighborhood of ε–1(y) such that q restricts to a homeomorphism of W onto its image by q (in X). We let V be p–1(q(W)). For every y’ in V’, we show that ε–1(y‘) is in W. Since q is a homeomorphism of W onto q(W), it suffices to show that q(ε–1(y‘)) is in q(W). This is now obvious: since q o ε–1 = p, this boils down to p(y’) ∈ q(W), which follows from the fact that y’ is in V = p–1(q(W)). ☐
The adjunctions whose counit is a natural isomorphism are a well known object, see Section 3 of the nCatLab entry on reflective subcategories. In particular, we learn that the monad LSect o E, from PreSh(X) to PreSh(X), with unit η, is idempotent; that LSect is fully faithful; and that Etale(X) is equivalent to its so-called essential image by LSect, which then turns out to be a reflective subcategory of PreSh(X). As usual with category theory, this involves quite a lot of notions, which will benefit from some concrete explanations.
The sheafification functor LSect o E
Let me recall that LSect(Y, p) is always a sheaf, not just a presheaf. It so happens that the essential image I just mentioned is the full subcategory Sh(X) of sheaves on X. This can be checked by hand by verifying the following series of lemmata.
Lemma A. Let F be a sheaf on X, with restriction map rUV : FV → FU for all pairs of open sets U⊆V. Let U, V be two open subsets of X, f ∈ FU, g ∈ FV, and let us assume that for every y in U ∩ V, f ≡y g (namely, there is an open neighborhood W of y included in both U and V such that rWU(f)=rWV(g)). Then r(U ∩ V)U(f) = r(U ∩ V)V(g).
Proof. For every y in U ∩ V, there is an open neighborhood W of y included in both U and V such that rWU(f)=rWV(g), and we call it W(y). The family of open sets W(y) forms an open cover of U ∩ V, when y varies over U ∩ V. The family C of elements rW(y)U(f), when y varies over U ∩ V, is trivially consistent, since it is the family of restrictions of a single element f. By the sheaf property, it must be the collection of restrictions to each W(y) of a unique element h of FU ∩ V. Since rW(y)U(f) is equal to rW(y)(U ∩ V)(r(U ∩ V)U(f)) for every y, that unique element h must be r(U ∩ V)U(f). C is also the family of elements rW(y)V(g), when y varies over U ∩ V, since rW(y)U(f)=rW(y)V(g). By a symmetric argument, the unique element h must be equal to r(U ∩ V)V(g), and the claim follows. ☐
Lemma B. Let F be a sheaf of X, and let s : U → S(X, F) be any local section of p : S(X, F) → X, where U is any open subset of X. There is a unique f ∈ FU such that s=f.
Let me recall that f(x) ≝ (x, [f]) for every x in U. Let me also recall from last time that the sets f(U), where U ranges over the open subsets of X, and f ranges over FU, form a base of the topology of S(X, F).
Proof. By definition, s maps every point x of U to (x, [fx]), for some element fx of FU(x), for some sufficiently small open neighborhood U(x) around x. The equivalence class [fx] of fx is with respect to ≡x, and I should probably write it as [fx]x to reflect this, but the notation would start to feel somewhat redundant. Still, we will have to be careful about this point below.
We will pick U(x) so small that it is included in U. Since p is a local homeomorphism, we can also pick U(x) so small that p restricts to a homeomorphism from some open neighborhood V(x) of s(x) to U(x): there is an open neighborhood V of s(x) such that p restricts to a homeomorphism from V onto p(V), and if needed, we replace U(x) by its intersection with the open set p(V), and we define V(x) as V ∩ p–1(U(x)). Since p o s = id, the inverse of p|V(x) is s|U(x).
Finally, we can replace V(x) by any basic open subset of it that still contains s(x). This means that we can assume that V(x) is actually of the form f(U’) for some open subset U’ of X and some element f of FU’. If that is so, then the image of f(U’) by p is U, and since the image of V(x) by p is U(x), we must have U’=U(x). Also, since s(x) is in V(x)=f(U(x)), we must have [fx]=[f], so V(x) is, in fact, equal to fx(U(x)).
This implies that, for every point x of U, for every y ∈ U(x), s(y)=(y, [fx]y). (Note that the definition of s(y) is (y, [fy]y), with a “y” as subscript to “f“, not “x“; I am claiming that you can put an “x” there, and this will make no difference.) Explicitly, s(y)=(y, [fy]y); since y is in U(x), s(y)=s|U(x)(y) is in V(x)=fx(U(x)), and is therefore of the form (y’, [fx]y’), for some point y’, which must of course be equal to y.
Hence, given any two points x and x’ in U, we obtain that for every y in U(x) ∩ U(x’), s(y) is both equal to (y, [fx]y) and to (y, [fx’]y), so that fx ≡y fx’. Lemma A tells us that r(U(x) ∩ U(x’))U(x)(fx) = r(U(x) ∩ U(x’))U(x’)(fx’). Therefore, as x varies in U, the family of elements fx ∈ FU(x) forms a consistent family. Since the open sets U(x) form an open cover of U, the sheaf property implies that there is a unique element f of FU such that fx=rU(x)U(f) for every x in U.
In particular, for every x in U, fx and f have the same restriction to U(x), showing that fx ≡x f. Therefore s(x) = (x, [f]), with the same f for all the points x in U. In other words, s=f. The fact that this f is unique is obvious. ☐
Theorem. For every presheaf F on X, the unit ηF : F → LSect(E(F)) at F of the adjunction E ⊣ LSect is an isomorphism of presheaves if and only if F is a sheaf.
Proof. Let me recall that a morphism in the category of presheaves on X is a natural transformation. Hence an isomorphism of presheaves is a natural isomorphism. If F is a sheaf, it is easy to see that any isomorphic presheaf will also be a sheaf. The interesting direction is to show that if F is a sheaf, then ηF is an isomorphism of (pre)sheaves.
For every open subset U of X, the component ηF,U of the natural transformation ηF at U maps every f ∈ FU to f : U → S(X, F); let me recall that f(x) ≝ (x, [f]) for every x in U. We need to show that ηF,U is a bijection. To this end, we consider an arbitrary local section s : U → S(X, F) of p, and we must show that s=f for some unique f ∈ FU. This is exactly what we proved in Lemma B. ☐
In particular, if the presheaf F we start with is already a sheaf, then F is already isomorphic to its sheafification LSect(E(F)), through ηF. The adjunction E ⊣ LSect then restricts to an adjunction equivalence of categories between the category Sh(X) of sheaves on X and the category Etale(X) of étale maps on X.
Because it arises from an adjunction, LSect o E is the functor part of a monad, the sheafification monad. It replaces a presheaf by the best sheaf that approximates it, and shows that the category Sh(X) of sheaves on X is a reflective subcategory of the category of presheaves on X.
What about streams, then?
Everything I have said until now is well known. I would like to apply this to streams and prestreams.
Last time, we had seen that we could start from a prestream (X, (⊑U)U ∈ OX), build its presheaf F of locally monotone maps to any prescribed poset P, and that F is a sheaf if and only (X, (⊑U)U ∈ OX) is a stream. I had also drawn pictures of the étale space S(X, F) of that sheaf in the case where the given stream is the directed circle, and that P is the Sierpiński poset {0 < 1}:
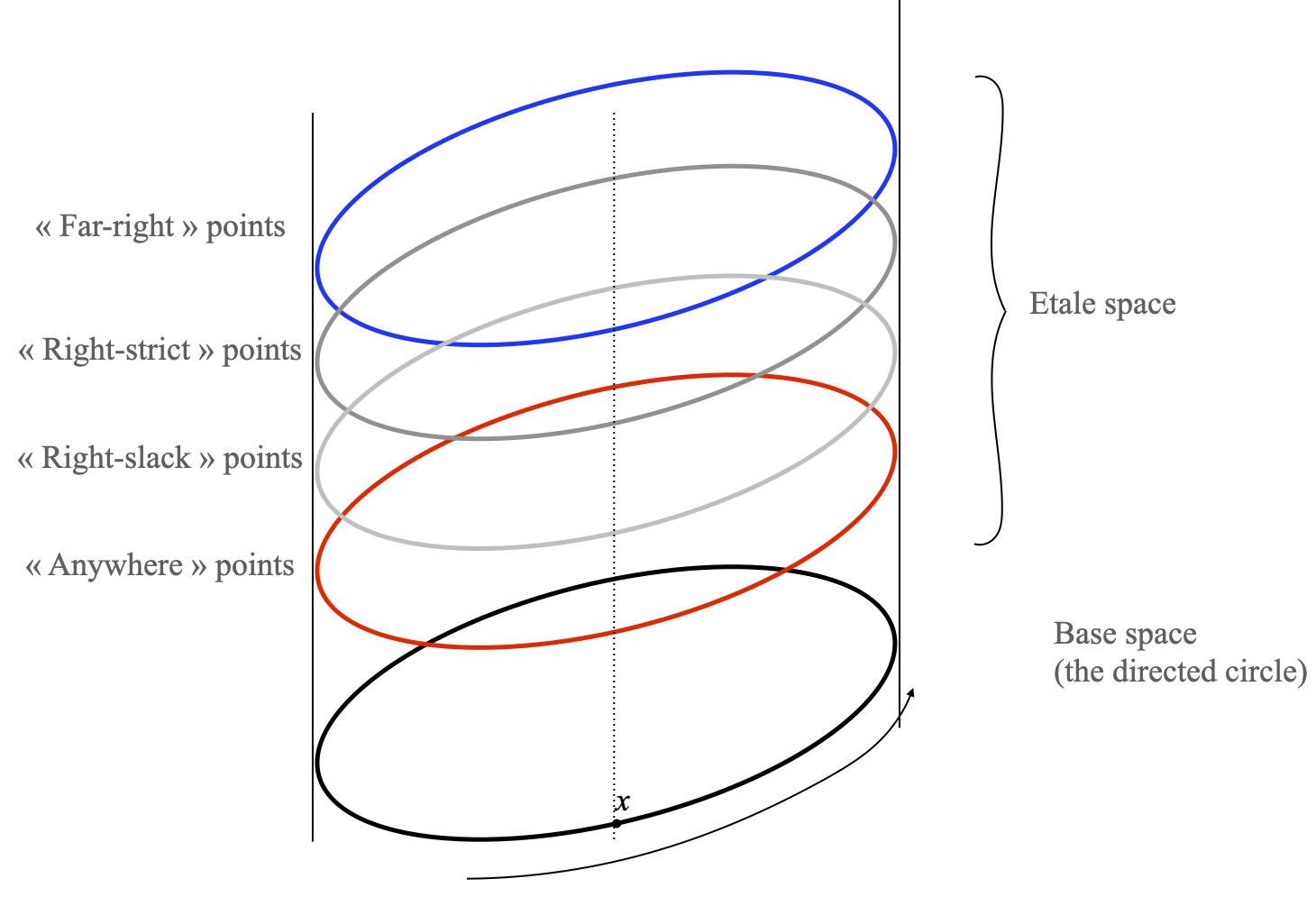
The étale space itself is the collection of four stacked circles on top, and the étale map p is projection down to the circle at the bottom.
Last time, we had observed that the stalks Fx = p–1({x}), at any point x, are ordered, by [f] ≤x [g] if and only if, for some sufficiently small open neighborhood W included in the domains of f and g, f|W ≤ g|W. May this is the start of some form of additional structure on the étale map (S(X, F), p) that would allow us to retrieve the whole stream, right? In other words, if I give you an arbitrary étale map (Y, p), plus some additional structure, surely you can reconstruct a sheaf from that, namely, LSect(Y, p), but maybe one could recognize that sheaf of local sections precisely as the sheaf of locally monotone maps for some circulation on X.
My impression is that the additional structure is not that ordering. Instead, it should simply be a map from Y to P, with some extra properties. Let us discover which. I am not completely happy with what follows, but that is certainly a solution.
Etale streams
When Y=S(X, F) and F is the sheaf of locally monotone maps from a prestream (X, (⊑U)U ∈ OX) to P, there is an obvious map from Y to P, which I will call eval: for every point (x, [f]) of S(X, F), let me define eval(x, [f]) as f(x). In the example of the directed circle, where we had in fact taken P to be {0 < 1}, eval maps the top two circles (“far-right” and “right-strict”) to 0, and the next two circles (“right-slack” and “anywhere”) to 1.
The definition of eval(x, [f]) as f(x) is independent of the choice of representative f in the equivalence class [f], because any pair of such representatives agrees on some open neighborhood of x, in particular on x itself. Diagrammatically, the situation is as follows.
For every open subset U of X, the local sections s : U → Y of p are exactly the maps f : x ↦ (x, [f]), where f ranges over the monotone maps from (U,⊑U) to P. We retrieve f as eval o s. In particular, this allows us to compare local sections by defining s ≤U s’ if and only if eval o s ≤ eval o s’, for all local sections s, s’ : U → Y of p; this mimics the usual pointwise ordering of monotone maps from (U,⊑U) to P. Although I will not mention that ordering explicitly below, it really subtends everything.
From now on, we will assume that P is a complete lattice. (This is certainly the case of {0 < 1}!) Then the collection of all the maps eval o s, where s : U → Y ranges over the local sections of p with domain U, is a complete lattice that is isomorphic to the complete lattice of all monotone maps from (U,⊑U) to P. Moreover, for every x ∈ U and for every a ∈ P, there is a local section s : U → Y such that (eval o s)(x)=a. There is an obvious one, which is the one such that eval o s is the constant map with value a. Perhaps more importantly, there is a smallest one; explicitly, for s that smallest local section, eval o s is characterized as mapping every x‘ ∈ U to a if x ⊑Ux’, and to the least element of P otherwise. We arrive at the following definition.
Definition. Let P be a fixed complete lattice, and X be a fixed topological space. A stratified étale map on X is a triple (Y, p, e), where Y is a topological space, and:
- p is a surjective local homeomorphism of Y onto X;
- e is a map from Y to P, such that for every open subset U of X:
- the collection of all maps e o s, where s ranges over the local sections of p with domain U, forms a complete lattice, where infima and suprema are computed pointwise;
- for all local sections s, s’ : U → Y of p such that e o s=e o s’, s=s’;
- and for every x ∈ U and for every a ∈ P, there is a local section s : U → Y of p such that (e o s)(x)=a.
We have just seen that, given any prestream (X, (⊑U)U ∈ OX), and letting F be its presheaf of locally monotone P-valued maps and p be first projection, (S(X, F), p, eval) is a stratified étale map (and item 2 is obvious).
Proposition. Let P be a fixed complete lattice, with least element 0 and largest element 1, and (Y, p, e) be a stratified étale map on X. For every open subset U of X, let the preordering ⊑U be defined by: for all x, x’ ∈ U, x ⊑U x’ if and only if, for every local section s : U → Y of p, (e o s)(x) ≤ (e o s)(x’). Then:
- for all x ∈ U and a ∈ P, there is local section cx,a : U → Y of p such that e o cx,a is the least map of the form e o s, where s ranges over the local sections of p with domain U such that (e o s)(x)=a;
- for all x, x’ ∈ U, x ⊑U x’ if and only if for every a ∈ P, (e o cx,a)(x’) ≥ a;
- the monotone maps f from (U,⊑U) to P are exactly the maps of the form e o s, where s ranges over the local sections of p with domain U, and for each each f, s is determined uniquely;
- (X, (⊑U)U ∈ OX) is a stream.
Proof. 1. There is a local section s : U → Y of p such that (e o s)(x)=a. Hence the set Lx,a ≝ {e o s | s : U → Y local section of p such that (e o s)(x)=a} is non-empty. Let cx,a be its infimum. Since infima are computed pointwise, e o cx,a maps x to a. Therefore e o cx,a is the least element of Lx,a.
2. If x ⊑U x’, then (e o s)(x) ≤ (e o s)(x’) for every local section s : U → Y of p. We use item 1, and we take s≝cx,a, where a is arbitrary: then (e o cx,a)(x)=a, so (e o cx,a)(x’) ≥ a. Conversely, let us assume that (e o cx,a)(x’) ≥ a for every a ∈ P. Let s : U → Y be an arbitrary local section of p with domain U. We let a≝(e o s)(x). By item 1, and the fact that e o cx,a is least, we have e o cx,a ≤ e o s. In particular, (e o s)(x) = a ≤ (e o cx,a)(x’) ≤ (e o s)(x’). Since s is arbitrary, x ⊑U x’.
3. For every local section s : U → Y of p, e o s is monotone by definition of ⊑U. Let us now consider any monotone map f from (U,⊑U) to P. Let L be the set {e o cx,a | x ∈ U, a ∈ P, a≤f(x)}. L has a supremum of the form e o s. Since suprema are computed pointwise and (e o cx,a)(x)=a for all x and a, we obtain that for every x ∈ U, (e o s)(x) ≤ f(x). Letting a≝f(x), e o cx,a is in L, and maps x to a, so (e o s)(x) is even larger; namely, (e o s)(x) ≥ f(x). Therefore (e o s)(x) = f(x), and this holds for every x ∈ U.
The fact that there is a unique s such that f = e o s is due to the fact that for all local sections s, s’ : U → Y of p such that e o s=e o s’, s=s’.
4. (X, (⊑U)U ∈ OX) is a prestream: for all open subsets U and V of X, for all points x, x’ of U such that x ⊑U x’, we consider any local section s : V → Y of p; its restriction s|U : U → Y is also a local section of p, and since x ⊑U x’, (e o s|U)(x) ≤ (e o s|U)(x’), so that (e o s)(x) ≤ (e o s)(x’); as s is arbitrary, x ⊑V x’.
Now Proposition A of last time shows that any prestream whose presheaf of locally monotone functions with values in {0<1} is a sheaf, is a stream. The same proof works verbatim if we replace {0<1} by any poset in which {0<1} embeds, and item 3 shows that the presheaf of locally monotone functions on X is isomorphic to the sheaf of local sections of (Y, p). Therefore (X, (⊑U)U ∈ OX) is a stream. ☐
From there, it should be easy to show that there is an equivalence between the category of streams on fixed topological space X and the category of stratified étale maps on X. There should really be not much to be done in addition to what we have done already. One most likely recovers the notion of cosheafification of a prestream by sheafifying its presheaf of locally monotone maps. But I have not checked that, and I should not make this post too long either: maybe another time, maybe not!
A last point on terminology
It is always hard to find a name for a new kind of structure. The adjective stratified in “stratified étale map” should have an intuitive meaning: for each a ∈ P, there is a stratum consisting of all those points y in Y such that e(y)=a (resp., eval(y)=a, for the stratified étale map of a prestream).
The literature already has notions of stratified spaces, see [2] or [3] for example, and the idea is roughly the same. A stratified space is a space Y with a map from Y to a poset P, satisfying some conditions. However, the conditions are very different from the ones I imposed; I decided that this would not prevent me from using the term “stratified”, as the conditions also vary wildly from one paper to the next. The simplest one is due to Dai Tamaki [2, Definition 2.1], and requires the map e from Y to P to be continuous, where P is given its Alexandroff topology.
Well, eval is continuous in no meaningful way, namely, only if P is given the coarse topology (or indiscrete topology: the topology whose only open sets are the empty set and P itself). This can be obtained by an analysis of the open subsets of S(X, F) for the sheaf F of locally monotone functions on the directed circle. Here are the four kinds of open neighborhoods of points of that étale space, which we had found last time:

This should be read as follows: we consider points (x, [f]), which can be on any of the four stacked circles that form the étale space of the directed circle (all except the bottom circle); depending on which of these circles it lies on, I have drawn an open neighborhood of that point in green. If (x, [f]) is in any of the two intermediate cases (the second and third stacks, from left to right), then that neighborhood contains (x, [f]), and that is the only point of that open neighborhood that lies on the same circle, and then it also contains a green region from the topmost (blue) circle to and a green region from the bottommost (red) circle of the stack. Looking at images by the eval map, (x, [f]) is sent either to 0 or to 1, but its open neighborhood contains a part in the blue circle, which gets sent to 0, and a part in the red circle, which gets sent to 1. This shows that neither eval–1({0}) nor eval–1({1}) is open. Therefore the only topology on P = {0 < 1} for which eval is continuous is the coarse topology.
- Jean Gallier and Jocelyn Quaintance. Homology, cohomology, and sheaf cohomology for algebraic topology, algebraic geometry, and differential geometry. December 2021. To be published, World Scientific. (Please mind the terms and conditions.)
- Dai Tamaki. Cellular stratified spaces. arXiv:1609.04500v1 [math.AT], September 15th, 2016.
- Jon Woolf. The fundamental category of a stratified space. arXiv:0811.2580v3 [math.AT], September 13th, 2013.

— Jean Goubault-Larrecq (December 20th, 2021)

