I initially wanted to talk about a few recent results of Jimmie Lawson [3]. But then I realized I should talk about Koch’s arc theorem first [1]. There is a proof of it in the red book [2, Exercises VI-5.16 through VI-5.18]. And then, I realized that I should talk about arc chains, the central notion of that theorem, and the relation between arc chains and arcs… and the fact that arc chains are, deep down, a purely order-theoretic notion; and all that will already be enough for one post. Here we go.
Arcs
The intuition behind the notion of an arc is the image of [0, 1], with its usual metric topology, by an injective continuous map f with values in some Hausdorff space. Any such image space (which I will write as f([0, 1])) must be compact and connected, since [0, 1] is, and since those properties are preserved by continuous maps. It must also be Hausdorff.
Finally, all its points except f(0) and f(1) are cut-points: if you remove any point f(t) from the image space f([0, 1]), you get a space that is no longer connected. Indeed, the resulting space is the union of the images f([0, t[) and f(]t, 1]), since f is injective. The complement of f([0, t[) in f([0, 1]) is the image f([t, 1]), and that is the image of a compact set by a continuous map; hence it is compact, and being compact in the Hausdorff space f([0, 1]), it is closed; so f([0, t[) itself is open in f([0, 1]). Similarly, f (]t, 1]) is open in f([0, 1]). The two sets f([0, t[) and f (]t, 1]) then form a partition of f([0, 1])–{f(t)} in two disjoint non-empty open sets, showing that f([0, 1])–{f(t)} is not connected. This completes our argument that all the points f(t) with 0<t<1 are cut-points. To the contrary, f(0) and f(1) are not cut-points, and since f is injective, they are disjoint.
Abstracting from this special case, we will define an arc as follows. This is the definition used by Koch, as far as I can tell [1].
Definition. An arc is a compact, connected Hausdorff space with exactly two non-cut-points.
The definition of an arc varies, and sometimes you will see that an arc is additionally required to be second-countable, or to be metrizable (that is equivalent, by Urysohn’s original metrizability theorem, see Exercise 6.3.18 in the book). We will not.
Example 0. (A silly example) A one-element set {a} is not an arc, because it does not have two cut-points. (In fact, it does not have any, because the empty set is connected, by definition.) But it is certainly compact, connected and Hausdorff.
Example 1. [0, 1] is, of course, an arc.
Counterexample 2. {0, 1}, with the discrete topology, is not an arc, as it is not connected: a partition in two disjoint non-empty open sets is given by {0} and {1}.
Counterexample 3. The circle S1, obtained as the subset of points at distance 1 to the origin in R2, is not an arc: none of its points is a cut-point. But S1 is compact, connected, and Hausdorff.
Counterexample 4. The collection of rational points in [0, 1] is not an arc: it is not compact (otherwise it would be as a subset of R, hence closed, but it is definitely not), and not connected (for any irrational number a such that 0<a<1, the set of rational points in ]a, 1] and the set of rational points in [0, a[ partition the space in two disjoint non-empty open sets).
I am mentioning this space because it is order-dense: inbetween any two distinct points, there is third one; and order density will play an important role later on in this post.
Example 5. We consider the (truncated) closed topologist’s sine curve. This is the set of points (x, y) of R2 such that:
- (left) x=0 and -1≤y≤1 (the vertical bar on the left),
- (right) or 0<x≤1/(2π) and y=sin(1/x).
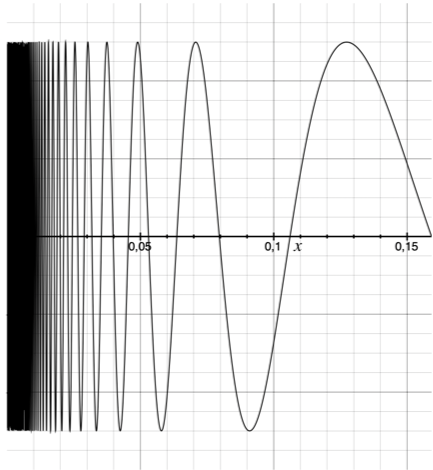
This space is really the closure of the (right) part in R2. It is closed and bounded in R2, hence compact. It is connected; I will let you prove it, this is a standard exercise (but you will need to know about path-connectedness—this space is itself an example of a connected, non-path-connected space). The rightmost point (1/(2π), 0) is a non-cut-point. All the other points in the (right) part are cut-points. And all the point in the (left) part are non-cut-points… so this space is not an arc, as its has more than two non-cut-points.
One may wonder at this point whether there are any arcs other than [0, 1], and the spaces that are homeomorphic to it. Look at the following one, and try to guess whether it is an arc, and if it is, whether it is homeomorphic to [0, 1]. (Answer below the picture.)
Example 6. Let us consider the subspace Xspring of R2 consisting of the points (x, y) such that:
- (left) -1≤x≤0 and y = 0
- (right) or 0<x≤1/(2π) and y=√x . sin(1/x).
I use √x to mean square root of x. This space looks as shown below: a variant of the topologist’s sine curve on the right, plus a horizontal line segment on the left.
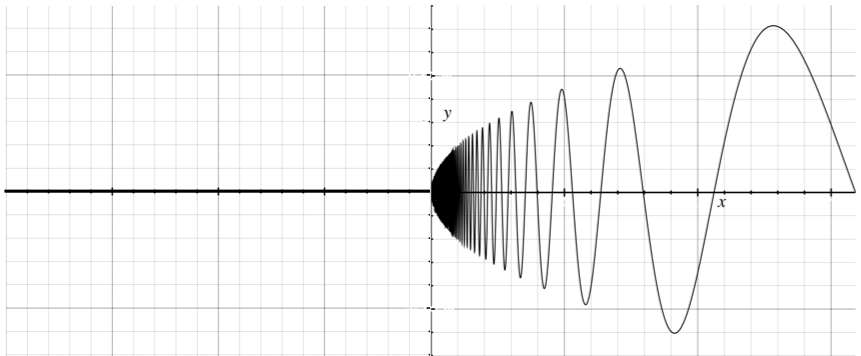
I claim that this space is an arc. Xspring looks rather different from [0, 1], but it is really homeomorphic to it; and this is why Xspring is an arc. Let f be the (continuous) function that maps every t ∈ [-1, 0] to 0 and every t ∈ ]0, 1/(2π)] to √t . sin(1/t). The function g : [-1, 1/(2π)] → R2 defined by g(t) = (t, f(t)) is then continuous, injective, and its image is Xspring. (Note added Feb. 10th, 2025: I previously claimed that f itself was injective, which is wrong; thanks to Xiaodong Jia for catching this.) By composing g with a suitable affine map, we obtain a continuous injective function from [0, 1] to R2, whose image is Xspring. Every continuous injective map from a compact space to a Hausdorff space is a topological embedding (Exercise 4.10.10 in the book), hence every continuous bijection from a compact space to a Hausdorff space is a homeomorphism, and that is the case of g.
Hence it seems that finding an arc that is not homeomorphic to [0, 1] is hard. Here is one.
Example 7. Let Lex be the set [0, 1]2, ordered lexicographically. Let us write <lex for that ordering: (x, y) <lex (z, t) if and only if x<z, or x=z and y≤t.
- Lex has a least element ⊥, namely (0, 0), and a largest element ⊤, namely (1, 1). We write [⊥, (x, y)[ for the set of points <lex (x, y), ](x, y), ⊤] for the set of points >lex (x, y). We equip Lex with the coarsest topology that makes those two kinds of sets open. (This generalizes to any poset, and is generally called the order topology.)
- We will see later that Lex, with that topology, is an arc, and its two cut-points are ⊥ and ⊤… Oh yes, sorry, we really have not learned enough to realize that Lex is an arc yet. We will see that in Remark N, at the very end of this post.
- Lex is not second-countable. Indeed, with the obvious notation for open intervals, the sets ](x, 1/3), (x, 2/3)[ are pairwise disjoint open subsets, and when x ranges over [0, 1], there are uncountably many of them. Given a base B of the topology, each point (x, 1/2) must have an open neighborhood included in ](x, 1/3), (x, 2/3)[, and therefore there are at least as many open sets in B as there are elements x of [0, 1].
- Since [0, 1] is second-countable, Lex is an arc that is not homeomorphic to [0, 1].
Lex is really a variant of the long line, which is best described on its Wikipedia article.
By Urysohn’s metrization theorem (Exercise 6.3.18 in the book), every second-countable T4 space is metrizable, and every compact Hausdorff space is T4 (Proposition 4.4.17 in the book). Hence every second-countable arc is metrizable. There is a theorem due to Oswald Veblen (according to this post on the Math Stackexchange) that says that every metrizable arc is homeomorphic to [0, 1]. Maybe we will see this next time.
Arc chains
An arc chain is a similar notion as an arc, except its elements are totally ordered. The ordering must also be compatible with the topology in a precise sense: it must be semiclosed, a notion we introduce right away.
A partial ordering ≤ on a topological space X is lower semiclosed if and only if ↓x is closed for every x in X; it is upper semiclosed if and only if ↑x is closed for every x in X. It is semiclosed if and only if it is both lower and upper semiclosed. For example, given any dcpo P, its ordering ≤ is lower semiclosed with respect to the Scott topology of ≤ (or with the Alexandroff topology, or with the upper topology), but in general not upper semiclosed. However, ≤ is semiclosed for P with its Lawson topology, because the Lawson topology explicitly requires ↑x to be closed for every point x.
In the book, there is a stronger notion (Definition 9.1.1): a pospace is a topological space X with an ordering ≤ whose graph (≤), namely the set of pairs (x, y) of points such that x≤y, is closed in X × X. The ordering ≤ of a pospace is always semiclosed. For a proof, we consider an arbitrary point x of X, and we aim to show that X – ↓x is open. For every y ∈ X – ↓x, (y, x) is in the complement of the closed set (≤), so (y, x) belongs to an open rectangle U × V that does not intersect (≤). Then U is an open neighborhood of y that is included in X – ↓x: otherwise there would be a point z in ↓x that would also be in U; hence (z, x) would be in U × V, and also in (≤), which is impossible. Similarly, X – ↑x is open. The argument is symmetric: for every y ∈ X – ↑x, (x, y) is in the complement of the closed set (≤), hence belongs to an open rectangle U × V that does not intersect (≤), and then y is in V, which is included in X – ↑x.
The converse certainly fails. There is probably a counterexample, but I did not find one. (I didn’t spend too much time on this, though. That is not central to our discussion, and the point will be moot anyway when talking about arc chains, as we will see in Proposition C below.)
Definition. An arc chain is a compact, connected topological space X of cardinality at least 2, with a semiclosed total ordering ≤.
Remark. (Warning: Reading this remark may leave your mind confused.) A semiclosed ordering on a topological space has sometimes been called semicontinuous, see for example Ward [4, p.145]; a topological space with what Ward calls a continuous partial ordering is what we call a pospace. We will refrain from using those names: in the book, and more generally in domain theory, a continuous poset is a poset in which every point is the supremum of a directed family of elements way-below it. This is a different notion. The funny thing (or the confusing thing) is that we will see later (Fact H) that arc chains really are certain continuous posets, in the domain-theoretic sense.
We will see that every arc chain is an arc. We first observe the following.
Lemma A. Given any non-empty compact space X with a semiclosed total ordering ≤, in particular any arc chain,
- every non-empty closed subset C of X has a least element and a largest element;
- X is a complete lattice with respect to ≤.
Proof. 1. We consider the sets ↓x where x ranges over C. Since ≤ is (lower) semiclosed, those sets are closed. If the intersection of all the closed sets ↓x ∩ C, when x ranges over C, were empty, then there would be finitely many points x1, …, xn in C such that ∩i=1n (↓xi ∩ C) is empty, since X is compact. If n=0, this would be the empty intersection, namely the whole of X, but that cannot be the case, since X is non-empty. Otherwise, ∩i=1n (↓xi ∩ C) is equal to ↓x ∩ C, where x is the least of the points x1, …, xn (which exists because ≤ is total), and that is non-empty since those point are all in C. Hence the intersection of all the closed sets ↓x ∩ C, when x ranges over C, is non-empty. Let us pick a point z in that intersection. By definition, z is in C, and z is smaller than or equal to every point x of C. Therefore z is the least element of C.
Symmetrically, and using the fact that ≤ is upper semiclosed, every non-empty closed subset of X has a largest element. Hence every subset of X has a greatest lower bound (an inf).
2. Let F be an arbitrary subset of X. Its collection of upper bounds is ∩x ∈ F ↑x is is closed, being an intersection of closed sets. By item 1, it must have a least element z. By definition, z is the least upper bound (the sup) of F. We reason symmetrically to show that F has a greatest lower bound (an inf); that is actually useless, since every poset in which every subset has a sup is such that every subset also has an inf. ☐
As a special case (take C ≝ X), an arc chain must have a least element, which we write as ⊥, and a largest element, which we write as ⊤.
Lemma B. In an arc chain (X, ≤), the only non-cut-points (if any) are ⊥ and ⊤. In other words, every point x of X different from ⊥ and from ⊤ is a cut-point.
Proof. We define U ≝ X – ↓x and V ≝ X – ↑x. Those are disjoint open sets. They are non-empty because x is different from ⊥ and from ⊤, and their union is X – (↓x ∩ ↑x) = X – {x}. Hence X – {x} is not connected, showing that x is a cut-point. ☐
It turns out that neither ⊥ nor ⊤ is a cut-point, but this requires some extra effort. We will only arrive at this conclusion in Proposition F below. In the meantime, let us establish some useful facts.
Arc chains are compact pospaces, and characterizing their topologies
To start with, I said that (quite likely) not every semiclosed ordering on a topological space turns it into a pospace. The situation is simpler with arc chains.
Proposition C. Every topological space X with a semiclosed total ordering ≤ is a pospace. In particular, every arc chain (X, ≤) is a compact pospace.
Proof. Let X be a topological space with a semiclosed total ordering ≤. Let (x, y) be a pair of points outside (≤). Hence x ≰ y. The set V ≝ X – ↑x is open since the ordering ≤ is semiclosed, and similarly the set U ≝ X – ↓y is open. Then (x, y) is in U × V, and U × V is included in the complement of (≤). Indeed, for every pair (x’, y’) of points in U × V, if (x’, y’) were in (≤), we would have x’ ≤ y’; but x’ is in U = X – ↓y, so x’ ≰ y, hence x’ > y since the ordering is total; similarly y’ is in V ≝ X – ↑x, so x ≰ y’, which means that x > y’ since the ordering is total. It follows that x > y’ ≥ x’ > y, in particular x ≰ y. We have shown that U × V is an open neighborhood of (x, y) included in the complement of (≤). Since this holds for every pair (x, y) in the complement of (≤), the complement of (≤) is open, hence (≤) is closed, as promised. ☐
This will imply that the topology of (X, ≤) is entirely determined by the ordering ≤.
In order to see this, we will use the theory of Nachbin duality between compact pospaces and stably compact spaces (see Section 9.1 of the book). Given a compact pospace (X, ≤), the space with the same points as X but with the upward topology, consisting of all ≤-upwards-closed open subsets of X, is a stably compact space. Let me write it as X↑. Additionally, the specialization ordering of X↑ is ≤, and the patch topology of X↑ is the original topology on X.
Given an arc chain (X, ≤), or more generally a compact space X with a semiclosed ordering ≤, I claim that the ≤-upwards-closed open subsets of X, namely the open subsets of X↑, are the half-open intervals ]a, ⊤], a ∈ X, plus X itself. The notation ]a, b] refers to the set of all points strictly larger than a and smaller than or equal to b, and I will also use the notations [a, b[, ]a, b[, [a, b]. In order to prove the claim, let U be an ≤-upwards-closed open subset of X, and C be its complement. If C is empty, then U must be the whole of X. Otherwise, by Lemma A, item 1, C has a largest element a. Since U is upwards-closed with respect to ≤, C is downwards-closed, and is therefore equal to ↓a = [⊥, a]; the complement of the latter is ]a, ⊤].
Let us call proper open subset of X any open subset of X other than X itself. We can write X as the interval [⊥, ⊤]. We will show that the remaining open sets, namely the proper open sets, are unions of o-intervals (for “open or half-open interval”), which I am defining as follows:
- any non-empty open interval, namely of the form ]a, b[ with a<b in X (if ]a, b[ is non-empty then certainly a<b, and we will see in Fact E, item 1 that the two conditions are equivalent),
- or a non-empty half-open interval [⊥, b[, with b≠⊥,
- or a non-empty half-open interval ]a, ⊤] (with a≠⊤).
Oh, I forgot: a<b means “a≤b and a≠b“—just to be sure we agree. I will also use the notation b>a.
Proposition D. For every compact space X with a semiclosed ordering ≤, in particular for every arc chain (X, ≤), the proper open subsets of X are exactly the unions of families F of o-intervals. We can require F to consist of pairwise disjoint non-empty o-intervals, of which at most one is of the form [⊥, b[ and at most one is of the form ]a, ⊤].
Proof. We have already discovered what the open subsets of X↑ are, using Proposition C and Lemma A. The open subsets of its de Groot dual (X↑)d, which by definition are the complements of compact saturated subsets of X↑, are also the open subsets of X that are ≤-downwards-closed, by the general theory of compact pospaces. By a symmetrical argument as above (or by considering the arc chain (X, ≥)), the open subsets of (X↑)d are therefore the half-open intervals [⊥, b[, b ∈ X, plus X itself. The open subsets of X are the open subsets in the patch-open topology, which is the coarsest topology generated by the open subsets of X↑ and of (X↑)d. The intersection of ]a, ⊤] with [⊥, b[ is ]a, b[ if a<b, and is empty otherwise. Hence the open subsets of X are exactly the unions of intervals, either of the form ]a, b[ with a<b, or [⊥, b[ or ]a, ⊤], namely, o-intervals.
Let U be a proper open subset of X. U is a union of o-intervals. It remains to see that one can turn any such union into a union of a family F of o-intervals that obeys all the constraints stated in the lemma, and which, notably, will consist of pairwise disjoint o-intervals.
For each x ∈ U, let Ix be the union of all the o-intervals containing x and included in U. We claim that Ix is also an o-interval. Any union of a family of open intervals ]ai, bi[, where i varies in some non-empty set I (and ai<x<bi), is equal to ]infi ∈ I ai, supi ∈ I bi[; indeed, a point y is outside this union if any only if either y≤ai for every i ∈ I, or y≤bi for every i ∈ I, if and only if y≤infi ∈ I ai or y≥supi ∈ I bi. Similarly, a union of a non-empty family of half-open intervals [⊥, bi[ is equal to [⊥, supi ∈ I bi[, and a union of a non-empty family of half-open intervals ]ai, ⊤] is equal to ]infi ∈ I ai,⊤] . Hence Ix can be written as ]a, b[ (if no o-interval containing x and included in U is half-open), or as a half-open interval, or as a union [⊥, b’[ ∪ ]a, b[ (which we can rewrite as [⊥, max(b, b’)[, since [⊥, b’[ and ]a, b[ overlap at x) or as a union ]a, b[ ∪ ]a’, ⊤] (which we rewrite as ]min(a, a’), ⊤]); it cannot be equal to a union of the form [⊥, b’[ ∪ ]a, b[ ∪ ]a’, ⊤] (with x in all three intervals), which would be equal to [⊥, ⊤], since we have assumed U proper.
Hence Ix is an o-interval: this is the largest o-interval containing x and included in U.
We claim that the family F consisting of the o-intervals Ix, where x varies over U, consists of pairwise disjoint o-intervals. Indeed, if Ix and Iy are distinct and intersect at some point z, then Ix ∪ Iy is an o-interval, too, or the whole interval [⊥, ⊤]. The latter is impossible, since we have assumed U proper. But Ix ∪ Iy contains x, so by maximality of Ix, Ix = Ix ∪ Iy. Similarly, Iy = Ix ∪ Iy, so Ix = Iy, which is absurd.
Finally, at most one of the o-intervals in F can be of the form [⊥, b[, and that is I⊥, and similarly at most one of the o-intervals in F can be of the form ]a, ⊤]. ☐
Order-density and (finally!) ⊥ and ⊤ are non-cut-points
We will now rely on the following fact. This relies on connectedness, a property we have not used for quite some time.
Fact E. Let (X, ≤) be an arc chain. Then:
- (X, ≤) is order-dense, meaning that for all x<y in X, there is a z in X such that x<z<y;
- given any two disjoint o-intervals I and I’, where I is of the form ]a, b[ with a<b or ]a, ⊤] with a<⊤, a does not belong to I’;
- given any two disjoint o-intervals I and I’, where I is of the form ]a, b[ with a<b or [⊥, b[ with ⊥<b, b does not belong to I’.
Proof. 1. Let us imagine that x<y, but that there is no point z in X such that x<z<y. Then [⊥, y[ and ]x, ⊤] are two disjoint open subsets of X, and their union is the whole of X, using the fact that ≤ is a total ordering. But none of these open subsets is empty, since [⊥, y[ contains x and ]x, ⊤] contains y. This is impossible because X is connected.
2. Let us imagine that a ∈ I’. We write I’ as ]a’, b’[ with a’<a<b’, or as [⊥, b’[ with a<b’. I’ cannot be of the form ]a’, ⊤] with a’<a, since otherwise it would contain I, hence in particular would intersect I, since every o-interval is non-empty by assumption. We have a<b’, whichever the form of I’ is. When I is of the form ]a, b[ with a<b, we obtain that a<min(b,b’).
By item 1, and since a<b’ (in the case I=]a, ⊤]; resp., a<min(b,b’) in the case I=]a, b[), there is a point z in X such that a<z<b’ (resp., a<z<min(b,b’)). Then z is both in I and in I’, a contradiction.
3. This is similar to item 2. ☐
Proposition F. In an arc chain (X, ≤), ⊥ and ⊤ are (the only) non-cut-points.
Proof. Let us imagine that ⊥ is a cut-point. Hence X – {⊥} is not connected. We can therefore partition X – {⊥} in two disjoint non-empty open sets, necessarily of the form U – {⊥} and V – {⊥} for two open subsets U and V of X. But U – {⊥} is equal to U – ↓⊥, which is open in X. Similarly, V – {⊥} is open in X. Let U’ ≝ U – {⊥} and V’ ≝ V – {⊥}: X – {⊥} is the union of the two non-empty disjoint open subsets U’ and V’ (open in X, that is). We use Proposition D and we write U’ as a union of a family F of pairwise disjoint intervals Ii, where i ranges over a non-empty index set I, and V’ as a union of a family G of pairwise disjoint intervals Ij, where j ranges over a non-empty index set J. Since U’ and V’ are disjoint, every Ii is disjoint from every Ij with j in J, so {Ii | i ∈ I} ∪ {Ij | j ∈ J} is a collection of pairwise disjoint intervals. Their union is X – {⊥} = ]⊥, ⊤], a proper open subset of X.
Let us pick any i ∈ I. Then Ii must be of the form ]a, b[ or ]a, ⊤]: it cannot be of the form [⊥, b[ because ⊥ does not belong to Ii. We have just seen that Ii is disjoint from every Ij with j in J, and Fact E, item 2, then tells us that a cannot be in any Ij with j in J. Hence a is not in V’. But a is not in U’ either, for the same reason: it is not in Ii by definition, and it cannot be in any Ii’ for any other index i’ in I, since Ii’ and Ii are disjoint, using Fact E, item 2. Therefore a is not in U’ ∪ V’, namely not in X – {⊥}, and it follows that a=⊥.
We have just obtained that every Ii with i ∈ I must be of the form ]⊥, b[ with ⊥<b or ]⊥, ⊤]. Hence U’ must contain of just one such o-interval. Indeed, we claim that if it contained two, then they would intersect, which is impossible since they are disjoint. In order to see this, the intersection of any two intervals ]⊥, b[ with ⊥<b (or ]⊥, ⊤]) and ]⊥, b’[ with ⊥<b’ (or ]⊥, ⊤]) must be of the form ]⊥, min(b,b’)[ (or ]⊥, b’[ or ]⊥, b[ or ]⊥, ⊤]), which cannot be empty, since X is order-dense (Fact E, item 1).
Similarly, V’ must consist of just one o-interval, of the form ]⊥, b’[ with ⊥<b’ or ]⊥, ⊤]. And then, as in the previous paragraph, U’ ∩ V’ must be non-empty. This is absurd, since U’ and V’ were chosen disjoint. Hence we must conclude that our initial assumption was wrong: ⊥ cannot be a cut-point.
Symmetrically, or replacing (X, ≤) with the arc chain (X, ≥), ⊤ is not a cut-point either. ☐
In particular, an arc chain has exactly two cut-points, so we have finally obtained:
Corollary G. For every arc chain (X, ≤), X is an arc, and its two non-cut-points are ⊥ and ⊤.
Order-dense pointed d-chains
We have seen that every arc chain (X, ≤) is order-dense (Fact E, item 1), and is a complete lattice (Lemma A, item 2). In particular, it is a pointed dcpo; pointed means that it has a least element ⊥.
It is also totally ordered. A chain is a totally ordered set, and we will call d-chain any chain that is a dcpo as well. A d-chain is a chain in which every directed family has a supremum, but since every non-empty family in a chain is directed, a d-chain is a chain in which every non-empty family has a supremum. Hence a pointed d-chain is the same thing as a chain in which every family has a supremum, namely a chain that is also a complete lattice. In particular, a pointed d-chain must have a top element ⊤, in addition to a bottom element ⊥.
It might be that ⊥=⊤, in which case our pointed d-chain will be reduced to one element. We will call non-trivial pointed d-chain any pointed d-chain with at least two elements.
In the August 2020 post, and precisely in Proposition A there, we noticed that every chain, namely every totally ordered poset (P, ≤) is a continuous poset, and that its way-below relation ≪ contains <, namely that for all points x and y in P, x<y implies x≪y. (Yes, “continuous” in the domain-theoretic sense, not in Ward’s sense.) We have already mentioned that every pointed d-chain is a complete lattice.
Fact H. Every pointed d-chain is a continuous complete lattice. If it is order-dense, then its way-below relation ≪ is given by x≪y if and only if x=⊥ or x<y.
The only thing that remains to be proved is that if x≪y and if x≠⊥, then x<y, under the assumption that the pointed d-chain is order-dense. We consider the collection D of points z<y. Since x≪y, we have x≤y, and since x≠⊥, D contains ⊥ and is therefore non-empty; being totally ordered, it is directed. If sup D<y, then by order density there is a point z such that sup D<z<y. By definition of D, z<y means that z is in D; this contradicts sup D<z. Hence sup D=y. Since x≪y, we must have x≤z for some z in D; then x≤z<y, so x<y, as we had claimed.
Every continuous complete lattice is stably compact (Fact 9.1.6 in the book), so every pointed d-chain (P, ≤) is stably compact in its Scott topology.
In order to set notations, we write Pσ for P with the Scott topology of its ordering ≤. We can form its Nachbin pospace ((Pσ)patch, ≤), and that is a compact pospace. In particular, (Pσ)patch is compact Hausdorff, and ≤ is a semiclosed ordering on it.
We will see that for every order-dense, non-trivial pointed d-chain (P, ≤), ((Pσ)patch, ≤) is an arc chain. The only thing that remains to be proved is that (Pσ)patch is connected. This will follow from the following result [2, Proposition VI-5.6, item (i)]. The proof there says that this works like in [0, 1], and indeed this is how the proof below will proceed.
Proposition I. Let (X, ≤) be a pospace. Every compact subset K of X of cardinality at least 2 that is totally ordered and order-dense with respect to ≤ is an arc chain, when considered as a subspace with the restriction ≤|K of ≤ to K as ordering.
Proof. K is compact, has cardinality at least 2. It remains to show that ≤|K is semiclosed, and that K is connected. For the former, we show that (K, ≤|K) is even a (compact) pospace: the graph (≤|K) of ≤|K is the intersection of the closed set (≤) with K × K, which is compact; so (≤|K) is compact in X × X, hence also in the subspace K × K.
Let us show that K is connected. As a subspace of X, K is compact with a semiclosed ordering ≤|K. Hence Lemma A, item 2 applies: K is a complete lattice with respect to ≤|K. This will allow us to take suprema in what follows.
Let us imagine that we can write K as a union of two disjoint non-empty open subsets U and V. We pick a point a from U and a point b from V. Exchanging U and V (and a and b) if necessary, and since ≤|K is total, we may assume that a<b. We let c be the supremum of {x ∈ U | x<b} in K, with respect to ≤|K. Since c is a supremum of points that are all less than or equal to b, we have c≤b. Now c is in K, hence is either in U or in V.
- Case 1: c is in U. We use Proposition D on the space K, ordered by ≤|K. Since V is non-empty, its complement U is a proper open subset of K, hence is a (disjoint) union of o-intervals. In particular, there is an o-interval I containing c and included in U. I cannot be of the form ]a’, ⊤] with a’<⊤ (and a’<c, because c is in I), since together with c≤b, this would entail that b is in I, hence in U; and that is impossible since b is in V and U and V are disjoint.
Hence I is of the form ]a’, b’[ with a’<b’ or [⊥, b’[ with ⊥<b’, and in both cases c<b’. We have c≤b, and c≠b because c is in U, b is in V, and U and V are disjoint. Hence c<b. Whichever of b and b’ is the smallest (let us remember that ≤|K is total), we have c<min(b,b’). We use order-density, and we find a point z such that c<z<min(b,b’). Since c<z<b’, z is in I, hence in U; since z<b, z is even in the set {x ∈ U | x<b} of which c is the supremum. This is impossible since c<z. - Case 2: c is in V. Using Proposition D as above, there is an o-interval I’ containing c and included in V. I’ cannot be of the form [⊥, b’[ with ⊥<b’ (and, necessarily, c<b’ since c is in I), since then a would be in I’, hence in V, contradicting the fact that it is in its complement U. Hence I’ is of the form ]a’, b’[ with a’<b’, or ]a’, ⊤] with a’<⊤. In both cases, a’<c, since c is in I’.
By order-density, there is a point z such that a’<z<c. In particular, the whole interval [z, c] is included in I’, hence in V. Since U and V are disjoint, no point of [z, c] can be in U. Hence the points in the set {x ∈ U | x<b}, which are all less than or equal to c by definition of c, cannot be larger than or equal to z. Since ≤|K is total, all the elements of {x ∈ U | x<b} are (strictly) less than z, so their supremum is less than or equal to z. But this supremum is c, by definition: we have obtained that c≤z. This direcly contradicts the fact that z<c.
We have reached a contradiction in both cases. Therefore U and V do not exist, showing that K is connected. ☐
As we had announced before Proposition I, we obtain the following.
Corollary J. For every order-dense, non-trivial pointed d-chain (P, ≤), ((Pσ)patch, ≤) is an arc chain.
The topology on (Pσ)patch has a simple description.
Lemma K. For every order-dense, pointed d-chain (P, ≤), the open subsets of (Pσ)patch are the unions of o-intervals.
Proof. By Corollary J, ((Pσ)patch, ≤) is an arc chain, hence the notion of o-intervals makes sense; let ⊥ be the least element of P, and ⊤ be its largest element.
By Fact H, P is a continuous complete lattice, and ≪ is characterized by x≪y if and only if x=⊥ or x<y. Hence the (Scott) topology of Pσ has a base of open sets of the form ↟a, namely ]a, ⊤] where a ranges over X–{⊥} or [⊥, ⊤].
We claim that the non-empty compact saturated subsets of Pσ are exactly the sets of the form ↑b with b in X. Those are certainly all compact saturated; conversely, any non-empty compact saturated subset Q has a minimal element b (see Lemma A of the February 2021 post, for example), which must be unique since the ordering ≤ is total, so Q=↑b.
Hence the topology of de Groot dual of Pσ (the cocompact topology), which consists of the complements of compact saturated subsets of Pσ, consists of P itself (=X), plus the complements of the sets ↑b with b in X, namely the sets [⊥, b[ with b in X.
It follows that the topology (Pσ)patch has a base of open sets consisting of the half-open intervals ]a, ⊤] and [⊥, b[, where a and b range over X (plus [⊥, ⊤], in principle, but as [⊥, ⊤] is already the intersection of the empty family, we do not need to include it in any base). This is what we wanted to prove. ☐
We sum up everything we have learned. This shows that arc chains can be presented as a purely order-theoretic notion. The whole topological side of the notion is already encoded in the ordering.
Theorem L (Arc chains≡order-dense non-trivial pointed d-chains). Given any arc chain (X, ≤), the poset (X, ≤) is an order-dense, non-trivial pointed d-chain. Given any order-dense, non-trivial pointed d-chain (P, ≤), ((Pσ)patch, ≤) is an arc chain. The two constructions are inverse of each other.
Proof. The first part is obtained by collecting item 1 of Fact E and item 2 of Lemma A, as argued at the beginning of the current section, together with the fact that X is non-trivial because an arc chain has two non-cut-points, hence must have cardinality at least 2. The second part is Corollary J. It remains to see that the two constructions are inverse of each other.
Given an order-dense, non-trivial pointed d-chain (P, ≤), the second construction forms X ≝ (Pσ)patch, keeping ≤ as ordering, then the first construction extracts the set of points of (Pσ)patch—that is just P—and produces (P, ≤).
Given an arc chain (X, ≤), the first construction produces the order-dense, non-trivial pointed d-chain (P, ≤) where P is simply X seen as a set, and the second construction applied to the latter produces ((Pσ)patch, ≤). We need to show that X = (Pσ)patch, namely that the topology of X is the patch topology obtained from the Scott topology on P. Lemma K says that the open subsets of (Pσ)patch are the unions of o-intervals, and Proposition D says that the open subsets of X are also the unions of o-intervals: hence the two topologies coincide. ☐
Remark M. I have used the patch topology here, but the Lawson topology would fit equally well, for the silly reason that the patch and Lawson topologies on Pσ coincide. This can be seen by realizing that every compact saturated subset of Pσ is either empty or of the form ↑b, as we have shown in the course of the proof above. Hence the cocompact topology coincides with the lower topology. Since the Lawson topology is the coarsest topology finer than the Scott and lower topologies, and the patch topology is the coarsest topology finer than the Scott and cocompact topologies, they coincide. More generally, the Lawson and patch topologies coincide on every continuous dcpo (see Exercise 9.1.36 in the book).
Remark N. The space Lex of Example 7 is an order-dense, non-trivial pointed d-chain. Perhaps the only fact in the previous sentence that would not be completely obvious is that it is a dcpo. We remember that the elements of Lex are those of [0, 1]2, ordered lexicographically. We consider a directed family D in Lex. Let A be {x | (x, y) ∈ D for some y}, and x∞ ≝ sup A. If x∞ ∉ A, then (x∞, 0) is the supremum of D in Lex. Otherwise, let B be {y | (x∞, y) ∈ D}, and y∞ ≝ sup B; then (x∞, y∞) is the supremum of D in Lex.
By Corollary J, it follows that Lex is an arc chain in the patch topology of its Scott topology. That patch topology consists of the unions of o-intervals, by Lemma K, so we retrieve exactly the topology that we had put on Lex in Example 7.
Finally, using Corollary G, we conclude that Lex is an arc, as we had claimed in Example 7.
- Robert Jacob Koch. Arcs in partially ordered spaces. Pacific Journal of Mathematics 9:723–728, 1959.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Jimmie Lawson. Chains in partially ordered spaces. Topology Proceedings 61:123–137, 2023.
- Lewis Edes Ward, Jr. Partially ordered topological spaces. Proceedings of the American Mathetical Society 5:144–161, 1954.

— Jean Goubault-Larrecq (January 20th, 2025)
