Compactly Choquet-complete spaces I: LCS-complete and Gδ subspaces

The purpose of this post and of those that will follow is to start a study of a notion introduced in [1]: the compactly Choquet-complete spaces. This will be an opportunity to examine a few techniques in topological game theory; and also, somewhat less gloriously, to fill in a few gaps in [1].

The strong Choquet game was invented by Gustave Choquet in order to characterize completely metrizable spaces [2]. Theorem 7.6.15 in the book states that for a subspace Z of a complete metric space X (with its open ball topology), it is equivalent to say that:

• Z is completely metrizable, namely there is a metric—in general unrelated to that of X—that makes Z complete and whose open ball topology coincides with the subspace topology induced by the inclusion in X,
• or that Z is a G_δ subset of X (a countable intersection of open subsets),
• or that Z is Choquet-complete, namely that player α has a winning strategy in the strong Choquet game on Z.

The notion applies outside the realm of metrizable spaces. For example, every continuous dcpo is Choquet-complete in its Scott topology (Lemma 7.6.3 in the book). This is crucial in Martin’s Theorem (Proposition 7.7.19, Theorem 7.7.21 in the book).

The strong Choquet game is described in Section 7.6 of the book. It is played between two players, α and β. Player β starts the game by picking a point x₀ and an open neighborhood V₀ of x₀. Then α replies with an open neighborhood U₀ of x₀ included in V₀; β picks a possibly different point x₁ in U₀, an open neighborhood V₁ of x₁ included in U₀; α replies with an open neighborhood U₁ of x₁ included in V₁; β picks a possibly different point x₂ in U₁, an open neighborhood V₂ of x₂ included in U₁, and so on. After both players have played for as many turns as there are natural numbers, α is declared to win if ∩_n ∈ N U_n (which is also equal to ∩_n ∈ N V_n) is non-empty. Otherwise, β wins.

Both players play according to strategies, which are functions that take all the points and open sets played until now, and tell you what next open set U_n to play (for α) knowing x₀, V₀, U₀, x₁, V₁, U₁, …, x_n–1, V_n–1 or what next point x_n and what next open set V_n to play (for β) knowing x₀, V₀, U₀, x₁, V₁, U₁, …, x_n–1, V_n–1, U_n–1 (for n=0, this tells β how to start the game). Giving a strategy σ for α and a strategy τ for β, there is a unique way to play the game.

A winning strategy for α is a strategy σ for α such that, whatever strategy τ player β uses, α will win the game. There is a symmetric notion of winning strategy for β.

There are many variants of this game. One can change the rules of the game itself, as in the Banach-Mazur game (Exercise 7.6.12 in the book). Even without changing the rules of the game, we can change the winning conditions.

For example, a convergent winning strategy for α is a strategy σ for α such that, whatever strategy τ player β uses, the sequence of open sets U_n played by α forms a base of open neighborhoods of some point x_∞. This was invented by Dorais and Mummert [3]. If there is such a convergent winning strategy for α, then ∩_n ∈ N U_n must be equal to the upwards closure ↑x_∞ of x_∞, and in particular must be non-empty. Hence a convergent winning strategy is winning in the original sense. A space is convergence Choquet-complete if and only if α has a convergent winning strategy. We have just argued that every convergence Choquet-complete space is Choquet-complete.

The continuous dcpo are not just Choquet-complete, they are convergence Choquet-complete (Exercise 7.6.6 in the book). Every Smyth-complete quasi-metric space, with its open ball topology, is convergence Choquet-complete (Exercise 7.6.5 in the book), while every Yoneda-complete quasi-metric space is Choquet-complete (Proposition 7.6.2 in the book). Among the T₀ spaces, the first-countable images of complete metric spaces under continuous open maps are exactly the convergence Choquet-complete spaces, and among the T₁ spaces, the images of complete metric spaces under continuous open maps are exactly the convergence Choquet-complete spaces (Exercise 7.6.20 the book; the second part is due to Dorais and Mummert [2]).

LCS-complete spaces

LCS-complete spaces were introduced and studied in [1], as one of the largest classes of spaces on which a certain measure extension theorem holds. LCS stands for “locally complete sober”: an LCS-complete space is a topological space X that is homeomorphic to a G_δ subspace of a locally compact sober space Y.

Let me reproduce a diagram from [1], showing the relation between LCS-complete spaces and various other classes of spaces. There are many classes of spaces here that I will not even try to define. An arrow from A to B means that every A is a B. Hence, for example, every locally compact sober space is LCS-complete (I guess that this much was obvious); every quasi-Polish space is LCS-complete, too.

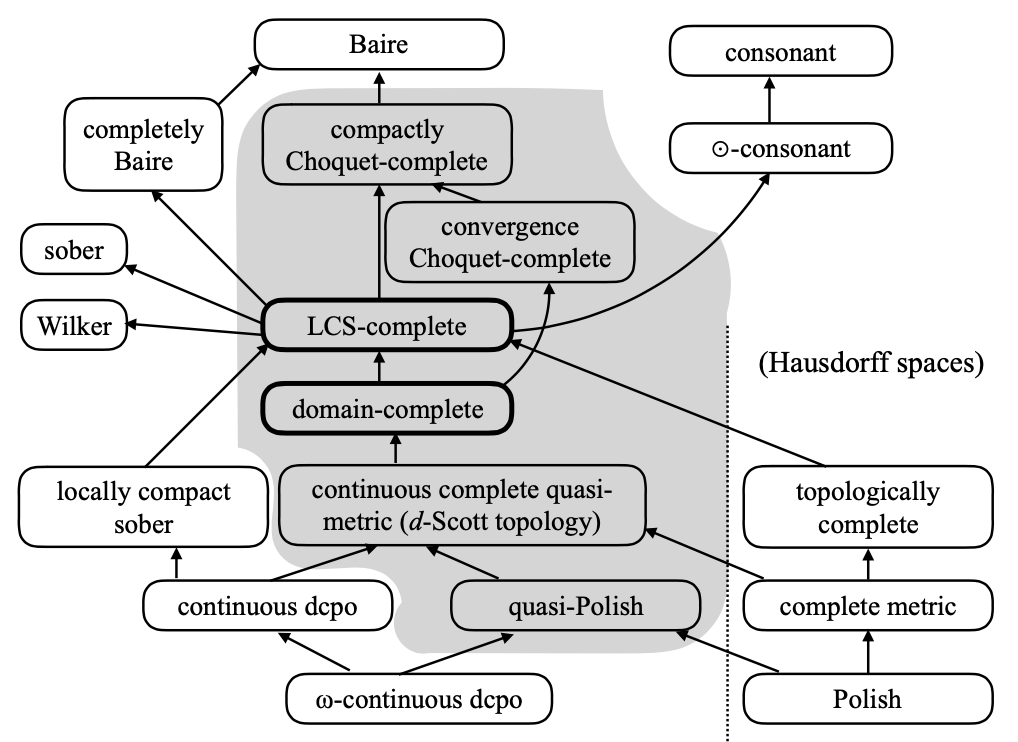
The point of the current post is to explain the “compactly Choquet-complete” box, to justify the arrow leading to it and going out of it, and to ask a few questions. Rongqi Xiao (肖荣奇) is working on related questions right now.

Compact Choquet-completeness

Since every continuous dcpo is convergence Choquet-complete, one may inquire whether this is also true for the larger class of LCS-complete spaces. In [1], we tried that and we only obtained that LCS-complete spaces satisfied a slightly weaker property, weaker than convergence Choquet-completeness but still stronger than Choquet-completeness. The notion and the argument are due to Matthew de Brecht.

Definition. A compactly winning strategy for α is a strategy σ for α such that, whatever strategy τ player β uses, the sequence of open sets U_n played by α forms a base of open neighborhoods of some non-empty compact subset Q_∞ (namely, Q_∞ is compact, non-empty, included in every U_n and every open neighborhood of Q_∞ is included in some U_n).
A space is compactly Choquet-complete if and only if α has a compactly winning strategy.

Clearly,

• Every convergence Choquet-complete space is compactly Choquet-complete: just let Q_∞ be ↑x_∞, where x_∞ is given in the definition of convergence Choquet-completeness.
• Every compactly Choquet-complete space is Choquet-complete: this is because Q_∞ is non-empty and included in ∩_n ∈ N U_n.

We will show that every LCS-complete space is compactly Choquet-complete below. In [1, Proposition 9.1], this is done directly, but: (1) there is a gap in the proof (we need to ensure that Q_n ⊆ int(Q_n–1) in addition to the other conditions on Q_n) (2) it is more elegant to do this in two steps: showing that every locally compact sober space is Choquet-complete first, then showing that the class of Choquet-complete spaces is closed under G_δ subspaces. The first step is easy, and we will do it right away. The second step is more complicated, and will require us to have a discussion on memoryfull and memoryless strategies.

Locally compact sober spaces

We will see that every locally compact sober space X is compactly Choquet-complete. In fact, player α even has a stationary compactly winning strategy, in the following sense.

A stationary strategy for α is one that only depends on the last pair x_n, V_n played by β, and we write σ(x_n, V_n) instead of σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) in that case (see Lemma 7.6.3 in the book). Note that σ(x_n, V_n) does not even depend on the length n of the history. A space is stationary compactly Choquet-complete (resp., stationary convergence Choquet-complete) if and only if α has a stationary compactly (resp., stationary convergently) winning strategy.

Proposition A. Every locally compact sober space X is compactly Choquet-complete; player α even has a stationary compactly winning strategy.

Proof. Given that β has just played x_n, V_n, α computes U_n ≝ int(Q_n) where Q_n is a compact neighborhood of x_n included in V_n. This is possible because Y is locally compact, and x_n is in V_n. At the risk of being pedantic, we need to make that into a stationary strategy σ, and to this end we need to define it as a choice function (using the Axiom of Choice) σ mapping every pair (x, V) where x is a point of X and V is an open neighborhood of x to a compact neighborhood of x included in V;

The list of points and open sets played during the game will be V₀ ⊇ Q₀ ⊇ U₀ ⊇ V₁ ⊇ Q₁ ⊇ U₁ ⊇ … In particular, Q_∞ ≝ ∩_n ∈ N Q_n is also equal to ∩_n ∈ N U_n.

Q_∞ is a filtered intersection of compact saturated subsets in the sober space X. Every sober space is well-filtered (Proposition 8.3.5 in the book), and in a well-filtered space every filtered intersection of compact saturated subsets is compact saturated (Proposition 8.3.6 in the book). Therefore Q_∞ is compact saturated in X.

Maybe I should recall (Proposition 8.3.5 in the book, just cited) that a well-filtered space is a space in which every filtered family of compact saturated subsets whose intersection is included in an open set U already contains an element that is included in U.

If Q_∞ were empty, then Q_∞ = ∩_n ∈ N Q_n would be included in the open set ∅, so some Q_n would be included in ∅. This is impossible since the interior int(Q_n), hence also Q_n itself, contains x_n. Therefore Q_∞ is non-empty.

Since Q_∞ = ∩_n ∈ N U_n, Q_∞ is included in every U_n. It remains to see that (U_n)_n∈N forms a base of open neighborhoods of Q_∞ in X. Let U be any open neighborhood of Q_∞ in X. Then U contains Q_∞ = ∩_n ∈ N Q_n, so by well-filteredness some Q_n is included in U. But U_n = int(Q_n) is then included in Q_n, hence in U. ☐

In order to show that every LCS-complete space (a G_δ subspace of a locally compact sober space Y) is compactly Choquet-complete, we will show that every G_δ subspace of a compactly Choquet-complete space is compactly Choquet-complete. There does not seem to be any hope that α can use a stationary strategy here. In fact, α will require a strategy that is fairly complicated to describe, and it will be practical to make a detour through memoryful strategies, which we introduce now.

A note on memoryful versus memoryless strategies

It is customary in game theory to not specify strategies formally (for player α, say), but to describe how α will play, in a more relaxed and leisurely way; e.g., « at step n, knowing that β has just played x_n, V_n, α will play U_n ≝ […] ».  This makes things more intuitive, but this is dangerous, and can hide a variety of mistakes.

One thing we sometimes do is let α compute U_n by first finding other objects, for example a compact saturated neighborhood Q_n of V_n containing x_n, and then defining U_n as the interior of Q_n, say.  This is what we did in the proof of Theorem A.

Sometimes we need to remember these auxiliary objects for future steps in the game.  (We did not have to do so in the proof of Theorem A.) For example, and this is essentially what the proof of Proposition 9.1 of [1] does, we might want to define U_n as some open subset of V_n, obtained by first finding some auxiliary compact saturated set Q_n, and intersected with int(Q_n–1) if n≥1, where we remember Q_n–1 from the previous step.

Now try to formalize this using the actual definition of strategies we have recalled above: you cannot.  Indeed, U_n must be obtained as a function σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) of the history x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n alone.  Whatever Q_n–1 you have produced at the previous step has been forgotten: σ is memoryless.

Here is one possible way of solving the issue.  We define a memoryful strategy (for α) as a function μ (μ for memory) that takes a pair consisting of a history x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n and a memory m (in some fixed set M), and returns a pair consisting of an open set U_n satisfying the usual conditions x_n ∈ U_n ⊆ V_n, and a new, updated memory m‘ ∈ M.  We also need an initial memory m₀.  We can now define what it means to play the strong Choquet game with a memoryful strategy:

• using its own strategy τ, player β produces x₀, V₀;
• from the current history x₀, V₀ and the initial memory m₀, α uses μ to compute U₀ and a new memory m₁;
• β now produces x₁, V₁ from the new history x₀, V₀, U₀  (no, β does not have access to α’s memory);
• from the current history x₀, V₀, U₀, x₁, V₁, and the memory m₁, α uses μ to compute U₁ and a new memory m₂;
• etc.

At the end, we decide whether α wins the game by the usual formula (compactly winning, convergent winning, etc.—let us say xxx-winning, whatever xxx may be), which disregards memories entirely.

Memoryful strategies are a practical expedient, but let me argue that if α has a xxx-winning memoryful strategy μ, then it also has a xxx-winning memoryless strategy σ.  (The converse implication is obvious: given a xxx-winning memoryless strategy, define the space M of memories as any one-element space {*}; the memoryful strategy σ that takes a history x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n and the unique possible memory * and returns σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) and the only possible memory * is xxx-winning.)

Here is how we define σ from μ. The value μ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n; m) is a pair (U_n; m’) consisting of an open subset U_n and a new memory m’.  We write μ₁(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n; m) for its first component U_n and μ₂(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n; m) for its second component m’.  We define σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) so that it computes the same open set U_n without having access to any memory by reconstructing the missing memories, by induction on n:

• The initial memory m₀ is given.
• For every i ∈ {1, …, n}, we reconstruct memory m_i as μ₂(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_i–1, V_i–1;m_i–1).
• Finally, we define σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) as μ₁(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n; m_n).

In other words, instead of storing a memory somewhere, we recompute it every time we need it.  It is easy to see that, during a play between α and β, whether α uses the memoryful strategy μ or the memoryless strategy σ, the same sequence of points and open sets x₀, V₀, U₀, x₁, V₁, U₁, …, x_n, V_n, … will be produced.

G_δ subspaces of compactly Choquet-complete spaces

As promised, we can now show that the class of compactly Choquet-complete spaces is closed under the formation of G_δ subspaces. We will need to know the following easy fact (and well-known—if you want to sound savant, say “compactness is absolute”).

Lemma B. Let Y be a subspace of a topological space X. The compact subspaces of Y are exactly the compact subspaces of X included in Y.

Proof. Let Q be compact in Y. For every open cover (U_i)_{i ∈ I} of Q in X, (U_i ⋂ Y)_{i ∈ I} is an open cover of Q in Y, from which we extract a finite subcover (U_i ⋂ Y)_{i ∈ J} (namely, J is a finite subset of I). Then (U_i)_{i ∈ J} is a finite subcover of Q in X.

Conversely, let Q be a compact subset of X that is included in Y. Every open subset of Y can be written as the intersection of an open subset of X with Y. Therefore an open cover of Q in Y is of the form (U_i ⋂ Y)_{i ∈ I} where each U_i is open in X, and (U_i)_{i ∈ I} is then an open cover of Q in X. Since Q is compact in X, it has a finite subcover (U_i)_{i ∈ J}. Then (U_i ⋂ Y)_{i ∈ J} is a finite subcover of Q in Y. ☐

Theorem C. Every G_δ subspace of a compactly Choquet-complete space is compactly Choquet-complete.

Proof. Let X be a compactly Choquet-complete space, and σ be a compactly winning strategy for player α on X. Let Y be a G_δ subset of X, with the subspace topology. We write Y as ∩_i ∈ N W_i, where each W_i is open in X.

For every n ∈ N and every point y ∈ Y, let W(n) be the intersection of all the open sets W_i with 0≤i≤n.

For every open subset V of Y, by definition we can write V as the intersection of Y with some open subset V’ of X. Among those subsets V’, there is a largest one, which is the union of all the open subsets of X whose intersection with Y is equal to (equivalently, included in) V. Let us call V for this largest open subset of X such that V ∩ Y = V.

We define a new memoryful strategy σ’ for α on Y as follows. Given a history y₀, V₀, U₀, y₁, V₁, U₁, ···, y_n, V_n (on the subspace Y), we form a mirror history y₀, V₀ ∩ W(0), U‘₀, y₁, V₁ ∩ W(1), U‘₁, ···, y_n, V_n ∩ W(n) on X. The open sets U‘₀, U‘₁, ···, U‘_n–1 are the memory. Player α will play according to σ on X, obtaining U‘_n ≝ σ(y₀, V₀ ∩ W(0), U‘₀, y₁, V₁ ∩ W(1), U‘₁, ···, y_n, V_n ∩ W(n)), and adding it to its memory right away. It will then play U_n ≝ U‘_n ∩ Y as the result of applying σ’.

Let τ be any strategy for β on Y. Letting α play according to σ’ and β play according to τ on Y (the σ’/τ scenario), we will obtain a series of points and open sets y₀, V₀, U₀, y₁, V₁, U₁, ···, y_n, V_n, U_n, ···, and we claim that we would obtain a related series of points and open sets y₀, V₀ ∩ W(0), U‘₀, y₁, V₁ ∩ W(1), U‘₁, ···, y_n, V_n ∩ W(n), U‘_n, ···, where U_n ≝ U‘_n ∩ Y for every n ∈ N, if we had let α play according to σ and β play according to some strategy τ’ on X that we will define right away (the σ/τ’ scenario).

Given a history x₀, V‘₀, U‘₀, x₁, V’₁, U’₁, ···, x_n–1, V’_n–1, U’_n–1 on X, τ’ first checks that the pair x₀, V‘₀ is equal to the pair y₀, V₀ ∩ W(0) where y₀, V₀ ≝ τ(); if so, it then checks that the pair x₁, V’₁ is equal to the pair y₁, V₁ ∩ W(1) where y₁, V₁ ≝ τ(y₀, V₀, U‘₀ ∩ Y); and so on, until it finally checks that the pair x_n–1, V’_n–1 is equal to the pair y_n–1, V_n–1 ∩ W(n–1) where y_n–1, V_n–1 ≝ τ(y₀, V₀, U‘₀ ∩ Y, y₁, V₁, U‘₁ ∩ Y, ···, y_n–1, V_n–1, U’_n–1 ∩ Y). If any of these checks fails, then we let τ'(x₀, V‘₀, U‘₀, x₁, V’₁, U’₁, ···, x_n–1, V’_n–1, U’_n–1) be any pair of a point and an open subset of X, for example x_n–1, U’_n–1; this is unimportant, because this case will never happen below. Otherwise, we let τ'(x₀, V‘₀, U‘₀, x₁, V’₁, U’₁, ···, x_n–1, V’_n–1, U’_n–1) be y_n, V_n ∩ W(n) where y_n, V_n ≝ τ(y₀, V₀, U‘₀ ∩ Y, y₁, V₁, U‘₁ ∩ Y, ···, y_n–1, V_n–1, U’_n–1 ∩ Y).

Let us check our claim. In the σ’/τ scenario (on Y),

• β plays y₀, V₀ ≝ τ();
• α responds with U₀ ≝ U‘₀ ∩ X where U‘₀ ≝ σ(y₀, V₀ ∩ W(0)), and keeps U‘₀ in memory;
• β plays y₁, V₁ ≝ τ(y₀, V₀, U₀);
• α responds with U₁ ≝ U‘₁ ∩ X where U‘₁ ≝ σ(y₀, V₀ ∩ W(0), U‘₀, y₁, V₁ ∩ W(1)) and keeps U‘₀ and U‘₁ in memory;
• etc.

In the σ/τ’ scenario (on X),

• β plays y₀, V₀ ∩ W(0) where y₀, V₀ ≝ τ() (the same y₀, V₀ as in the σ’/τ scenario);
• α responds with σ(y₀, V₀ ∩ W(0)), namely with the same U‘₀ as in the σ’/τ scenario; then the set U₀ played in the σ’/τ scenario is equal to U‘₀ ∩ Y;
• β checks that the current history x₀, V‘₀, U‘₀ is such that x₀=y₀ and V‘₀=V₀ ∩ W(0), and therefore produces y₁, V₁ ∩ W(1) where y₁, V₁ ≝ τ(y₀, V₀, U‘₀ ∩ Y); since U₀ ≝ U‘₀ ∩ Y, this pair y₁, V₁ is the same as in the σ’/τ scenario;
• α responds with σ(y₀, V₀ ∩ W(0), U‘₀, y₁, V₁ ∩ W(1)), and that is the same U‘₀ as in the σ’/τ scenario; then the set U₁ played in the σ’/τ scenario is equal to U‘₁ ∩ Y;
• etc.

Since σ is compactly winning, the open sets U’_n form a base of open neighborhoods of a non-empty compact subset Q_∞ ≝ ∩_n ∈ N U’_n of X. But every U’_n played by α is included in the last open set V_n ∩ W(n) played by β (in the σ/τ’ scenario), hence is included in W(n); so Q_∞ is included in ∩_n ∈ N W(n) = ∩_i ∈ N W_i = Y. Every compact subset that is included in Y is also compact in the subspace Y (by Lemma B), so Q_∞ is compact in Y.

For every n ∈ N, Q_∞ is included in U’_n, and Q_∞ is included in Y, so Q_∞ is included in U’_n ∩ Y = U_n. In order to see that the sets U_n form a base of open neighborhoods of Q_∞ in Y, let U be any open neighborhood of Q_∞ in Y. Then U = U ∩ Y and U is an open neighborhood of Q_∞ in X. The sets U’_n form a base of open neighborhoods of Q_∞ in X, so one of them is included in U. Then U_n = U’_n ∩ Y ⊆ U ∩ Y = U. ☐

Corollary D ([1, Proposition 9.1]). Every LCS-complete space is compactly Choquet-complete.

Proof. An LCS-complete is, up to homeomorphism, a G_δ subspace of a locally compact sober space. A locally compact sober space is compactly Choquet-complete by Proposition A and taking a G_δ subspace preserves compact Choquet-completeness by Theorem C. ☐

I remember that Matthew de Brecht was somehow disappointed by not being able to show that every LCS-complete space is convergence Choquet-complete. And you cannot! The following counterexample is Remark 9.3 of [1], and is due to Zhenchao Lyu.

Counterexample E. (An LCS-complete, hence compactly Choquet-complete, that is not convergence Choquet-complete.) We take an uncountable set I, for example the set of all real numbers. We equip the two-element set {0, 1} with the discrete topology, and we form the space {0,1}^I with the product topology. This is a compact Hausdorff space. In particular, it is locally compact and sober, hence LCS-complete, hence compactly Choquet-complete. But no point of {0,1}^I has a countable base of open neighborhoods (a well-known fact, which I will reprove right below), and if {0,1}^I were convergence Choquet-complete, then α would have a winning strategy guaranteeing the existence of a point x_∞ with a countable base of open neighborhoods U_n, contradiction.
I said I would explain why no point of {0,1}^I has a countable base of open neighborhoods. In fact, we can show the even stronger statement: (∗) for every point a of {0,1}^I, every countable family of open neighborhoods (V_n)_n∈N of a must be such that ∩_n ∈ N V_n ≠ {a}. This is proved as follows. Let us write a_i for the ith component of a. For each subset J of I, let V_J(a) be the collection of points b in {0,1}^I that agree with a at all coordinates of J (a_i=b_i for every i ∈ I). This is a basic open subset of the product topology if J is finite. Since a ∈ V_n, there is a finite subset J_n of I such that a ∈ V_Jn(a) ⊆ V_n. Then ∩_n ∈ N V_n contains ∩_n ∈ N V_Jn(a), which is equal to V_J(a) where J ≝ ∪_n ∈ N J_n. But J is countable, so V_J(a) is the collection of points of {0,1}^I that agree with a at countably many coordinates (only). There are infinitely many points in V_J(a), and therefore there are also infinitely many points in the larger set ∩_n ∈ N V_n; hence ∩_n ∈ N V_n cannot contain just a.

The case of second-countable spaces

Counterexample E relies on an uncountability argument. For second-countable, compact Choquet-completeness does coincide with convergence Choquet-completeness, as we will see. This was stated in [1, Proposition 9.4].  There is a gap in the proof, which I will fill in.

At the end of the proof, we will need the following observation, already mentioned in the February 2021 post: the supercompact saturated subsets of a topological space X are exactly the sets of the form ↑x, x ∈ X. By definition, a subset Q of X is supercompact if and only if every open cover (U_i)_i ∈ I of Q in X contains an element U_i such that Q ⊆ U_i.

Let me first state an easier version of [1, Proposition 9.4] first, in order to show some of the techniques more clearly.

Theorem F (stationary version).  A second-countable space X is stationary compactly Choquet-complete if and only if it is stationary convergence Choquet-complete.

Proof.  Every stationary convergent winning strategy is a stationary compactly winning strategy.  Conversely, let σ be a stationary compactly winning strategy for α.  We will build an improved stationary strategy σ’ for α.

Since X is second-countable, it has a countable base B ≝ (B_n)_n∈N of open subsets, meaning that every open subset of X can be written as a union of sets B_n.  For every natural number n and every point x in X, let B(x,n) be the intersection of those sets among B₀, …, B_n that contain x. This is certainly open, and contains x.

Let us fix a strategy τ for β.  (This one is not forced to be stationary, and has access to the whole history.)  At step n of the strong Choquet game, and using strategy τ, β has just played a point x_n in X and an open neighborhood V_n of x_n in X (such that V_n is included in U_n–1 when n≥1).  If α played according to σ, it would produce σ(x_n, V_n).  We define U_n ≝ σ'(x_n, V_n) as σ(x_n, V_n ∩ B(x_n, n)) instead.  The important point is that we would get exactly the same open subset U_n if α were playing according to the original strategy σ, but β was playing according to a modified strategy that returns V_n ∩ B(x_n, n) instead of V_n.

It is also important that we take the intersection of V_n with B(x_n, n) first, then compute σ(x_n, V_n ∩ B(x_n, n)). Computing σ(x_n, V_n) ∩ B(x_n, n) instead would lead nowhere (try it if you are not convinced).

Now let Q_∞ ≝ ∩_n ∈ N U_n, as obtained by letting α play according to σ’ and β play according to τ.  Since the sets U_n are the same if we let instead α play according to σ and β play according to τ’, and since σ is a compactly winning strategy, Q_∞ is compact, non-empty, clearly saturated, and the sets U_n form a base of open neighborhoods of Q_∞.  (This was asserted without justification in the proof of Proposition 9.4 of [1].  I guess you will agree that this deserved an explanation.)

We now claim that: (*) given any two open sets U and V whose union contains Q_∞, Q_∞ must already be included in U or in V.  By definition of the countable base B ≝ (B_n)_n∈N, both U and V are unions of elements from B.  Since Q_∞ is compact and is included in U ∪ V, there are two finite subsets I and J of N such that ∪_i ∈ I  B_i ⊆ U, ∪_j ∈ J  B_j ⊆ V, and Q_∞⊆ (∪_i ∈ I  B_i) ∪ (∪_j ∈ J  B_j).  Since the sets U_n form a base of open neighborhoods of Q_∞, one of them will be included in (∪_i ∈ I  B_i) ∪ (∪_j ∈ J  B_j); then all the sets U_n for n larger than that will also be included in (∪_i ∈ I  B_i) ∪ (∪_j ∈ J  B_j).  Hence we can pick n as large as we wish so that U_n ⊆ (∪_i ∈ I  B_i) ∪ (∪_j ∈ J  B_j); and we choose n larger than every element of I ∪ J.  Since the point x_n played at step n is in the open set U_n, by definition of the strong Choquet game, it is in (∪_i ∈ I  B_i) or in (∪_j ∈ J  B_j).  If x_n ∈ ∪_i ∈ I  B_i, then x_n ∈ B_i for some i ∈ I (in particular, i≤n), so x_n ∈ B(x_n, n), by definition of B(x_n, n) as the intersection of the sets B_i that contain x_n and such that 0≤i≤n.  By definition of the strategy σ’, U_n ≝ σ'(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) is equal σ(x_n, V_n ∩ B(x_n, n)) and is therefore included in V_n ∩ B(x_n, n), hence in B(x_n, n), hence in B_i, hence in the larger set ∪_i ∈ I  B_i, which is itself included in U.  Therefore Q_∞ ⊆U_n ⊆ U.  By symmetry, if x_n ∈ ∪_j ∈ J  B_j instead, then Q_∞ ⊆ V.  This finishes to prove (*).

It follows from (*) that if Q_∞ is included in a union of k open sets with k≥1, then Q_∞ is included in one of them, by induction on k.

We now claim that Q_∞ is supercompact.  Let (W_i)_i ∈ I be an open cover of Q_∞.  Since Q_∞ is compact, it has a finite subcover.  Since Q_∞ is non-empty, this finite subcover must be by a non-zero number k of open sets W_i.  As we have just seen, Q_∞ must then be included in one of them, namely in some W_i.

Since Q_∞ is supercompact, as we have recalled before the statement of Theorem C, Q_∞ must be equal to ↑x_∞ for some point x_∞.  Every open set U_n played during the game must contain Q_∞, hence x_∞.  For every open neighborhood U of x_∞, we have ↑x_∞ ⊆ U, namely Q_∞ ⊆ U.  Since the sets U_n form a base of open neighborhoods of Q_∞, Q_∞ ⊆U_n ⊆ U for some n ∈ N.  In other words, x_∞ ∈ U_n ⊆ U.  Therefore the sets U_n form a base of open neighborhoods of x_∞. ☐

The previous theorem is a baby version of the actual theorem: it is unrealistic to restrict ourselves to stationary strategies, since for example the strategy we built in the proof of Theorem C is not stationary; we built it as a memoryful strategy, and even though it appears to be stationary (except for the use of an auxiliary memory), the compilation process to a memoryless strategy makes it non-stationary.

Theorem G (full version, [1, Proposition 9.4]). A second-countable space X is compactly Choquet-complete if and only if it is convergence Choquet-complete.

Proof.  Convergence Choquet-completeness implies compact Choquet completeness, so we concentrate on the converse implication.  We assume that α has a compactly winning strategy σ, and we will build a better strategy σ’ that will be a convergent winning strategy.  The idea is the same as in Theorem F (stationary version), but the details will be more complex.

Since X is second-countable, it has a countable base B ≝ (B_n)_n∈N of open subsets, we write B(x,n) for the intersection of those sets among B₀, …, B_n that contain x, and we define σ’ so that at step n of the strong Choquet game, if β has just played x_n, V_n, then σ’ will do as though β had just played V_n ∩ B(x_n, n) and apply σ, as before.

The difficulty is that now σ can see the whole history; in playing using σ’, the history will contain V_i ∩ B(x_i, i) at all steps i<n, and then α will call σ on that, while if we were playing using σ throughout, the history would have V_i at the same position.  We have to modify histories so that we get the same pairs x_n, U_n at each step n of the game, whether α plays according to σ’ and β play according to τ or α plays according to σ and β plays according to τ’.  Once we achieve that, the rest of the proof is as with Theorem F (stationary version): Q_∞ ≝ ∩_n ∈ N U_n is compact, non-empty and the sets U_n form a base of open neighborhoods of Q_∞, because they are obtained by letting α play according to the compactly winning strategy σ (whatever β uses—here, τ’), then we argue that Q_∞ is supercompact as before, and this will conclude the proof.

The difficulty sketched above was completely missed in the proof of Proposition 9.4 of [1], where is was claimed that σ'(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) should be equal to σ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n ∩ B(x_n, n)).  Instead, we need to define σ'(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n) as σ(x₀, V₀ ∩ B(x₀, 0), U₀, x₁, V₁ ∩ B(x₁, 1), U₁, ···, x_n, V_n ∩ B(x_n, n)), to reflect the fact that we must have played V_i ∩ B(x_i, i) instead of V_i at all steps i<n.

We wish to show that this strategy σ’ is compactly winning against all possible strategies τ that player β may use. In order to do so, we will show that letting α play according to σ’ and β play according to τ, we will obtain the same points x_n, and the same open sets U_n as though α were playing according to σ, but β were playing according to a possibly different strategy τ’. Since σ is compactly winning against all possible strategies that β may use, it will be compactly winning against τ’ and therefore σ’ will be compactly winning against τ.

The strategy τ’ of player β is a bit tricky to define.  Given a history x’₀, V’₀, U₀, x’₁, V’₁, U₁, ···, x’_n, V’_n, U_n as input, the idea is that τ’ should compute x_n+1, V_n+1 ∩ B(x_n+1, n+1) where x_n+1, V_n+1 is what τ would have returned.  But τ requires a history x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n, and it is unclear how we might compute appropriate values for x₀, V₀, x₁, V₁, ···, x_n, V_n from x’₀, V’₀, U₀, x’₁, V’₁, U₁, ···, x’_n, V’_n, U_n. so that V’_i = V_i ∩ B(x_i, i) for every i<n.  Instead of computing them, we will reconstruct them by playing the game according to the very strategy τ’ that we are defining, on smaller histories, recursively.  This is as in the compilation from memoryful strategies to memoryless strategies (for α), except for β this time.

Explicitly, given a history x’₀, V’₀, U₀, x’₁, V’₁, U₁, ···, x’_n, V’_n, U_n as input, τ’ first computes x₀, V₀ ≝ τ().  If x₀≠x’₀, then τ’ immediately returns an arbitrary point x’_n+1 and an arbitrary open set V’_n+1 meeting our needs (included in U_n and containing x’_n and x’_n+1, for example x’_n and U_n themselves); this is the unimportant part, because the condition we will always have x₀=x_’0 in an actual play.  Hence we assume that x₀=x’₀.  Then τ’ computes x₁, V₁ ≝ τ(x₀, V₀, U₀).  If x₁≠x’₁, then once again we let τ’ return an arbitrary point x’_n+1 and an arbitrary open set V’_n+1 meeting our needs.  We therefore assume that x₁=x’₁, and we continue in the same way until we have generated x_n+1, V_n+1 ≝ τ(x₀, V₀, U₀, x₁, V₁, U₁, ···, x_n, V_n): then τ’ returns x_n+1, V_n+1 ∩ B(x_n+1, n+1).

Let us check that letting α play according to σ’ and β play according to τ or letting α play according to σ and β play according to τ’, we obtain lists of points and open sets played with the same points x_n and the same open sets U_n. If α plays according to σ’ and β plays according to τ (the σ’/τ scenario), we generate:

• x₀, V₀ ≝ τ();
• U₀ ≝ σ(x₀, V₀ ∩ B(x₀, 0)), because that is what σ’ returns on x₀, V₀;
• x₁, V₁ ≝ τ(x₀, V₀, U₀);
• U₁ ≝ σ(x₀, V₀ ∩ B(x₀, 0), U₀, x₁, V₁ ∩ B(x₁, 1);
• etc.

When α plays according to σ and β plays according to τ’ instead (the σ/τ’ scenario), we obtain the following list of points and open sets:

• x₀, V’₀ where x₀, V₀ ≝ τ() and V’₀ ≝ V₀ ∩ B(x₀, 0) (yes, the same x₀, V₀ as in the σ’/τ scenario, but we produce V’₀ instead of V₀);
• σ(x₀, V’₀), and that is equal to the set U₀ obtained in the σ’/τ scenario;
• x’₁, V’₁ where x’₁, V’₁ ≝ τ'(x₀, V’₀, U₀); now, following the definition of τ’, this is obtained by reconstructing x₀, V₀ = τ(), then x₁, V₁ ≝ τ(x₀, V₀, U₀) and letting x’₁ ≝ x₁ and V’₁ ≝ V₁ ∩ B(x₁, 1);
• σ(x₀, V’₀, U₀, x₁, V’₁), and that is equal to U₁;
• etc.

I should really do a formal induction over n here, but I guess the above argument suffices to convince you that we get the same pairs x_n, U_n in both scenarios.  As we have announced, we finish the proof as with Theorem F (stationary version): Q_∞ ≝ ∩_n ∈ N U_n, is compact, non-empty, and the sets U_n form a base of open neighborhoods of Q_∞, because they were obtained by letting α play according to the compactly winning strategy σ (and β play according to some strategy τ’, which no longer matters at this point).  Then Q_∞ is supercompact, and we conclude. ☐

Matthew de Brecht had proved that the quasi-Polish spaces are exactly the second-countable, convergence Choquet-complete T₀ spaces [4, Theorem 51].  (To be precise, he shows this for non-empty spaces.  But the empty space is quasi-Polish, and also convergence Choquet-complete: α has a convergent winning strategy for the silly reason that β has no way of playing any point; therefore there is no strategy τ for β at all, and the winning condition « for every strategy τ for β, … » is then vacuously true.)

1. Matthew de Brecht, Jean Goubault-Larrecq, Xiaodong Jia, and Zhenchao Lyu. Domain-complete and LCS-complete Spaces. In Proceedings of the International Symposium on Domain Theory (ISDT’19), volume 345 of Electronic Notes in Theoretical Computer Science, pages 3–35, Yangzhou, China, June 2019. Elsevier Science Publishers. doi:10.1016/j.entcs.2019.07.014.
2. Gustave Choquet. Lectures on Analysis. Mathematics Lecture Note Series, vol. I – Integration and Topological Vector Spaces. W.A. Benjamin, Inc., 1969.
3. François G. Dorais and Carl Mummert. Stationary and Convergent Strategies in Choquet Games. Fundamenta Mathematicae 209:59–79, 2010.
4. Matthew de Brecht. Quasi-Polish spaces, Annals of Pure and Applied Logic 164:356–381, 2013.

— Jean Goubault-Larrecq (August 20th, 2025)