We have talked about arcs and arc chains in the last two posts of January and February 2025. Let me concentrate on arc chains, namely compact, connected topological spaces X of cardinality at least 2, with a semiclosed total ordering ≤. By semiclosed, we mean that the downward closure and the upward closure of any point is closed. However, instead of looking at arc chains in isolation, we will look at arc chains embedded in a pospace.
A pospace (X, ≤) is a topological space X with a partial ordering ≤ whose graph (≤) is closed in X2. In particular, X is Hausdorff (Proposition 9.1.12 in the book). In every pospace, ≤ is in particular semiclosed. We will consider arc chains inside a pospace (X, ≤), namely arc chains (A, ≤|A) where A arises as a subspace of X and ≤|A is the restriction of ≤ to A. Hence, contrarily to the last posts, we will not have the choice of an ordering to put on A.
Koch’s arc theorem [1, Theorem 2] is a famous theorem saying that, under a few conditions, given any point x of an open subset U of a pospace (X, ≤), one can draw an arc chain from some point on the boundary of U to x. I will state the theorem more precisely below.
The boundary ∂E of a set E is its closure minus its interior; hence the boundary of an open set U is ∂U ≝ cl(U)–U. By drawing an arc chain from a point a to x, I mean that there exists an arc chain (C, ≤|C) embedded in (X, ≤) whose least element is a and whose largest element is x.
The conditions needed for this theorem to hold are, first, that the closure cl(U) be compact in X; and second, that U does not contain any local minimum. A local minimum in a pospace (X, ≤) is a point x of X that is isolated in the downward-closure ↓x of x with respect to ≤; in other words, such that {x} is open in the subspace ↓x; equivalently, such that there is an open neighborghood O of x such that O ∩ ↓x = {x}. Hence U contains no local minimum if and only if for every x ∈ U, every open neighborhood O of x contains a strictly smaller point.
The precise statement of the theorem is as follows. I have taken the version of [3, Theorem 4.5], which is slightly more precise than the one in the red book [2, Theorem VI-5.9] or than Koch’s original version [1, Theorem 2].
Theorem (Koch’s arc theorem). Let U be an open subset of a pospace (X, ≤), and x be a point of U. If cl(U) is compact and if U contains no local minimum of ≤, then there is an arc chain embedded in (X, ≤), from some point of the boundary ∂U to x. Additionally, we can require the arc chain to be included in cl(U).
Remark A. The assumption that cl(U) is compact is automatic if (X, ≤) is a compact pospace. Conversely, in order to prove Koch’s arc theorem, we can reason in the subspace cl(U) of X. Then (cl(U), ≤) will be a compact pospace. Hence, replacing X by cl(U) if necessary, we can prove Koch’s arc theorem by requiring (X, ≤) itself to be a compact pospace, and U to be a dense open subset in X. This is what we will do in the final section of this post.
The proof can be found in [1], of course, and also in the red book [2], as a series of exercises (VI-5.16 through VI-5.18). I really mean that the proof is given there: the hints given in the exercises (almost) form the complete list of arguments that are needed. Let us work it out in detail.
Why the assumptions are necessary
If U contains a local minimum, the conclusion of the theorem fails.
Counterexample 1. The simplest counterexample is given by taking X ≝ {0, 1}, with the discrete topology and 0<1, x ≝ 1, and U ≝ {1}. Then the boundary ∂U is empty, since U is not just open but also closed, and the conclusion of the theorem then fails trivially.
Remark B. As the previous counterexample may have put into light, Koch’s arc theorem implies that an open subset with compact closure and containing no local minimum of its ambient Hausdorff space X (considering X as the pospace (X, =)) must have a non-empty boundary.
Counterexample 2. For a slightly less trivial counterexample, let X be the subspace [0, 1] ∪ [2, 3] of R, with its usual metric topology, and its usual ordering. Let x ≝ 2, U ≝ ]0.5, 1] ∪ [2, 2.5[, see below.
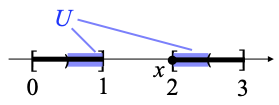
U is open because it is equal to the intersection of ]0.5, 2.5[ with X. The closure of U in X is [0.5, 1] ∪ [2, 2.5], and the only two points in its boundary ∂U are 0.5 and 2.5. There is no arc chain from 2.5 to x, since 2.5 is not below x (=2). There is no arc chain from 0.5 to x either: such an arc chain should consist of the points above 0.5 and below x, namely [0.5, 1] ∪ {2}, which is not connected; alternatively, it is not order-dense, since it contains no point strictly between 1 and 2, and we have seen in the January 2025 post that every order-chain is order-dense.
The assumption that cl(U) is compact is needed, too.
Counterexample 3. Let X be the subspace ]0, 1] ∪ [2, 3] of R, with its usual metric topology, and its usual ordering. Let x ≝ 2, U ≝ ]0, 1] ∪ [2, 2.5[, see below.
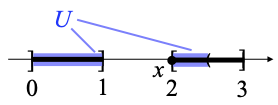
U is open because it is equal to the intersection of ]0, 2.5[ with X. Its closure cl(U) (in X) is equal to ]0, 1] ∪ [2, 2.5]: note that the latter is indeed closed in X, being the intersection of [0, 2.5] with X.
We check that cl(U) is not compact in X as follows. If it were compact, it would also be compact in R (Exercice! every compact subset K of a subspace A of a space B is compact in B), hence closed in R since R is Hausdorff. But ]0, 1] ∪ [2, 2.5] is not closed, since the sequence of numbers 1/2n with n ∈ N has no limit in that set.
Now we verify that there is no arc chain from a point of ∂U to x in X. We have just computed cl(U), and from that we see that ∂U = {2.5}. But there is no arc chain from 2.5 to x=2, since 2.5 is not below 2.
Maximal chains
Among the many equivalents of the Axiom of Choice, we find Zorn’s Lemma, and the Hausdorff maximality theorem (Theorem 2.4.1 in the book): given any chain C in a poset P, C is included in some maximal chain in P. A chain is a totally ordered, non-empty subset of P, and it is maximal if and only if adding any new element (outside of the chain) to it produces something that is no longer a chain, equivalently if and only if every element outside the chain is incomparable with at least one element of the chain.
Here is one idea we might have to prove Koch’s theorem—as we will see, a pretty good idea, but one that does not go the whole way. Given a point x in an open subset U (with compact closure, and containing no local minimum) of a pospace (X, ≤), we consider the poset P ≝ ↓x ∩ cl(U). We use the Hausdorff maximality theorem on the chain {x}, and we obtain a maximal chain C containing x and included in P. This chain consists of points below x, and contains x, so x is its largest element. We may now hope to show that C extends so far down as to contain a point of the boundary ∂U, and to show that C is an arc chain. In particular, C should be order-dense. But that may fail if ≤ is not already order-dense on X, as the following counterexample shows.
Counterexample 4 (the Swiss Flag). Let X be [0, 5]2 – ((]1, 4[ × ]2, 3[) ∪ (]2, 3[ × ]1, 4[)), with the usual metric topology, and ordered by the product ordering. This is the gray region depicted below, including the boundaries, shown in black. (This is familiarly called the Swiss Flag, and I hope you will forgive me for coloring it gray instead of red [really Pantone 485C], and for the wrong proportions of the cross.) X has exactly two local minima, the points (0, 0), at the bottom left, and d ≝ (3, 3); I have drawn two little arrows pointing at them.
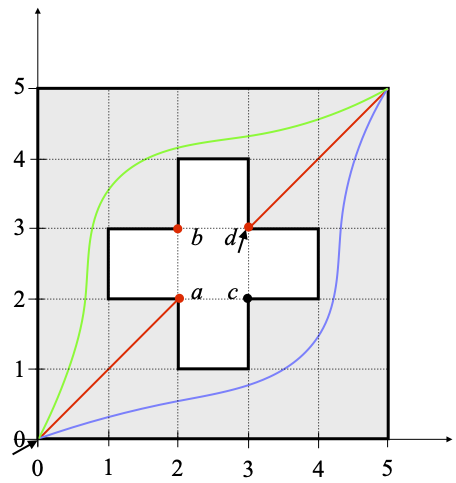
Let U consist of all the points of X except for those on the boundary of its cross-shaped hole and for those on its left and bottom external sides, namely ]0, 5]2 – (([1, 4] × [2, 3]) ∪ ([2, 3] × [1, 4])), or equivalently X intersected with the open set (]0, ∞] × ]0, ∞]) – (([1, 4] × [2, 3]) ∪ ([2, 3] × [1, 4])). This is an open subset of X, with compact closure (indeed, cl(U)=X), and containing no local minimum—indeed, it excludes both (0, 0) and d=(3, 3). The red region is the chain of points (x, x) with x ∈ [0, 2] ∪ [3, 5], plus the point b ≝ (2, 3). This is a maximal chain from (0, 0) to (5, 5)—please do not forget to include b in order to ensure maximality—but it is not order-dense, as there is no point strictly between b and d (or between a and b). Hence this maximal chain is not an arc chain. The green and blue chains, on the contrary, are order-dense.
A few properties of (maximal) chains
Still, taking maximal chains is not totally a bad idea. For example, Lemma C below implies that a maximal chain in a compact pospace must be compact. Considering that we are looking for arc chains, which are compact connected subspaces with exactly two non-cut-points, this takes care of compactness. In a series of further results, we will realize that the only thing we need to make sure that a maximal chain is an arc-chain is to require that it be order-dense. And indeed, the failure of order-density was the issue in the Swiss Flag example.
The following can found in [3, Lemma 3.4], where references to earlier sources of similar results are given.
Lemma C. The closure of a chain in a pospace (X, ≤) is a chain. Hence every maximal chain is closed.
Proof. Let C be a chain in a pospace (X, ≤). Let ≥ be the opposite ordering of ≤; since (≤) is closed, so is (≥). Let x and y be two incomparable points of cl(C). Hence (x, y) is in the open set (X × X) – (≤) and in the open set (X × X) – (≥), hence in their intersection (X × X) – ((≤) ∪ (≥)). We find an open rectangle U × V containing (x, y) and included in (X × X) – ((≤) ∪ (≥)). Then U intersects cl(C) at x, V intersects cl(C) at y, so U intersects C, say at some point x’, and V intersects C at some point y’. We obtain that (x’, y’) is in (X × X) – ((≤) ∪ (≥)), meaning that x’ and y’ are incomparable. This is impossible since x’ and y’ are on the chain C. Hence cl(C) is a chain.
Given a maximal chain C, cl(C) is also a chain. By maximality, C=cl(C), so C is closed. ☐
The next lemma is imitated from the construction of Scott’s dcpo IR (Exercise 4.2.28 in the book). Later in this post, we will apply this to the case where Y is a maximal chain in a space X with a semiclosed partial ordering ≤.
Lemma D. Let Y be a compact space with an semiclosed total ordering ≤. We define the set I(Y) of all (non-empty) closed intervals [a, b] with a, b ∈ Y and a≤b, and we order it by reverse inclusion ⊇.
- In I(Y), [a, b] ⊇ [c, d] if and only if a≤c and b≥d.
- I(Y) is a dcpo. For every directed family ([ai, bi])i ∈ I in I(Y), its supremum is the unique non-empty closed interval [a, b] that arises as the intersection ∩i ∈ I [ai, bi].
- Given a closed subset C of Y, the collection ♢C of elements [a, b] of I(Y) that intersect C is Scott-closed in I(Y).
Proof. 1. If [a, b] ⊇ [c, d], then c and d are in [a, b], hence in particular a≤c and b≥d. If a≤c and b≥d, then for every x ∈ [c, d], a ≤ c ≤ x and x ≤ d ≤ b, so [a, b] ⊇ [c, d].
2. Let ([ai, bi])i ∈ I be a directed family in I(Y), namely a filtered family of closed intervals, and let A ≝ ∩i ∈ I [ai, bi]. Each closed interval [ai, bi] is closed in Y, since it is equal to ↑ai ⋂ ↓bi, and ≤ is semiclosed. It is also non-empty by assumption. Every filtered intersection of non-empty closed subsets of a compact space is non-empty (see Proposition 4.4.9 in the book). It is also closed, being an intersection of closed sets. Hence it is compact, being a closed subset of the compact space Y.
Being compact as a subset, A is also compact as a subspace (Exercise 4.9.11 in the book). By Lemma A of the January 2025 post, every non-empty compact space with a semiclosed total ordering is a complete lattice, and in particular has a least and a largest element; let a be the least element of A and b be its largest element. (In particular, a≤b.) For every i ∈ I, [ai, bi] is order-convex: given three points x≤y≤z with x, z ∈ [ai, bi], y is also in [ai, bi]. It is easy to see that any intersection of order-convex sets is still order-convex, so A is order-convex. Since A contains a and b, it must therefore contain the whole interval [a, b]. The reverse inclusion is by definition of a and b, so A = [a, b].
Hence A = [a, b] is an element of I(Y). It is clear that A is an upper bound of ([ai, bi])i ∈ I, and that any upper bound of ([ai, bi])i ∈ I must be included in A. Therefore A is the supremum of ([ai, bi])i ∈ I, and I(Y) is a dcpo.
3. Let C be a closed subset of Y. For every element [a, b] of ♢C, for every smaller (with respect to reverse inclusion) element [c, d] ⊇ [a, b], [c, d] also intersects C, so [c, d] ∈ ♢C. Hence ♢C is downwards-closed. Given any directed family ([ai, bi])i ∈ I of elements of ♢C, its supremum in I(Y) is ∩i ∈ I [ai, bi], as we have shown in item 2. Each set [ai, bi] is closed and intersects C, which is compact, since it is a closed subset of the compact space Y. Every filtered intersection of closed subsets that each intersect a given compact set also intersects that compact set (Proposition 4.4.9 in the book), so ∩i ∈ I [ai, bi] ∈ ♢C. ☐
The next result is essentially item 1 of Proposition VI-5.6 in the red book [2], except that instead of assuming that (X, ≤) is a pospace, we only assume that ≤ is semiclosed. Also, the proof given there is pretty implicit.
Lemma E. A compact chain C in a space X with a semiclosed ordering ≤ is connected if and only if it is order-dense.
Proof. If C is connected but not order-dense, then there are two points x<y in C with no point strictly inbetween. Using this plus the fact that the ordering ≤ is total on C, ↓x and ↑y form a partition of C in two (non-empty) subsets. Those two subsets are closed because ≤ is semiclosed. Therefore C is not connected, which is absurd.
In the converse direction, let us assume that C is (compact,) order-dense but not connected. Since it is not connected, we can partition C as D ∪ E, where D and E are disjoint, non-empty closed subsets of C. There is a point in D, and one in E, and since ≤ is total on C, one of them is strictly smaller than the other. Up to symmetry, we assume a point a0 in D and b0 in E such that a0<b0. Then [a0, b0] ∈ I(C).
We observe that [a0, b0] intersects D at a0, and E at b0, so [a0, b0] ∈ ♢D ⋂ ♢E.
By Lemma E, I(C) is a dcpo under reverse inclusion, and ♢D ⋂ ♢E is Scott-closed. In particular, ♢D ⋂ ♢E is closed under directed suprema, and is therefore an inductive poset, so we can apply Zorn’s Lemma: there is a maximal element [a, b] of ♢D ⋂ ♢E above any given point, for example [a0, b0].
Let us assume that a<b. Since C is order-dense, there is a point t of C such that a<t<b. Because C = D ∪ E, t is in D or in E. If t ∈ D, then we pick u ∈ [a, b] inside E; such a u exists because [a, b] ∈ ♢D ⋂ ♢E. Then [t, u], or [u, t] depending on whether t<u or u<t, is in ♢D ⋂ ♢E, and is a proper subset of [a, b]: if t<u, this is because a<t, so a ∉ [t, u], and if u<t, this is because t<b, so b ∉ [u, t]. In other words, [t, u]—or [u, t]— is strictly above [a, b], and in ♢D ⋂ ♢E; this is impossible, since that contradicts the maximality of [a, b]. We reach a similar contradiction with [a, t] if t ∈ E instead. Hence it cannot be the case that a<b after all; and therefore a=b.
Now the fact that [a, b] ∈ ♢D ⋂ ♢E means that a (=b) is both in D and in E, which is impossible since D and E are disjoint. Hence our initial assumption that C was not connected must be false. ☐
We finally obtain the result we promised at the beginning of this section: the only thing that may prevent a (non-trivial) maximal chain in a compact pospace from being an arc chain is that it may fail to be order-dense.
Proposition F. Let C be a maximal chain in a compact space with a semiclosed partial ordering ≤, and let C contain at least two elements. Then C is an arc chain if and only if it is order-dense.
Proof. We have already seen that arc chains are order-dense (Fact E, item 1 of the January 2025 post). Conversely, if C is a maximal chain in a compact space with a semiclosed partial ordering, then it is closed by Lemma C, hence compact. If C is order-dense, it is connected by Lemma F. Since C contains at least two elements, C is an arc chain. ☐
Extending pospace orderings
Hence, instead of simply taking maximal chains in a pospace (X, ≤), we need to make sure that our maximal chains are order-dense, too. That was what failed in Couterexample 4 (the Swiss Flag example).
In order to do so, we will modify the ordering ≤ on the space X in such a way that all maximal chains will be order-dense. We will do this by replacing ≤ by the ordering ≤’V, W defined below, for some choice of pair of disjoint open subsets V and W, and repeating the process for transfinitely long, until we reach an ordering that can no longer be improved. This transfinite iteration will be done later—implicitly, really, through one (more) use of Zorn’s Lemma.
Lemma G. Let (X, ≤) be a compact pospace, and V and W be two disjoint open subsets of X. We define the new relation ≤’V, W by x ≤’V, W y if and only if x≤y and (if x ∈ V and y ∈ W then there is a point t ∈ X–(V ∪ W) such that x≤t≤y). Then:
- ≤’V, W is a partial ordering included in ≤;
- the graph (≤’V, W ) of ≤’V, W is closed in X × X, so (X, ≤’V, W) is a compact pospace;
- the local minima of (X, ≤’V, W) are the same as those of (X, ≤).
This is Exercise VI-5.16 of [2], where ≤’V, W is written as ⪯. Before I give the proof, let me illustrate this on the Swiss Flag. There is no point strictly between b and d, and we pick V and W so as to be disjoint open neighborhoods of those two points, as shown below.
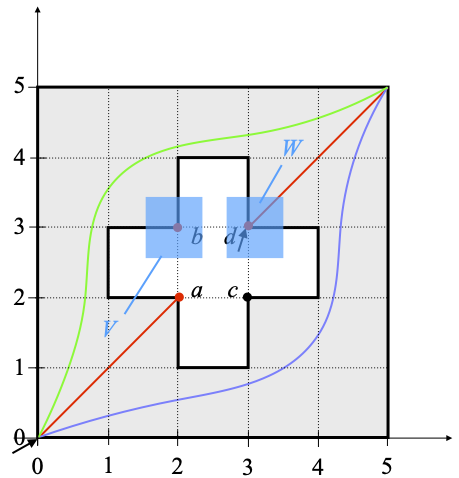
In the new partial ordering ≤’V, W, b is no longer below d. In fact, no point of X ⋂ V is below any point of X ⋂ W, because there is no point t in the “gray minus blue” region X–(V ∪ W) between any point of V and any point of W. The arrows pointing to the right in the picture below intend to describe this: the top two arrows are ways of going up along ≤ that are still allowed with ≤’V, W, and the struck out arrow below is one way of going up along ≤ that is no longer allowed with ≤’V, W.
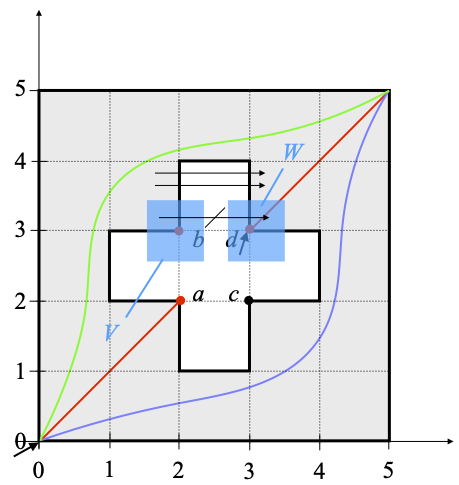
Proof. 1. That ≤’V, W is included in ≤, namely that for all points x and y, x ≤’V, W y implies x≤y, is clear. Reflexivity boils down to checking that for every point x of X, (if x ∈ V and x ∈ W then there is a point t ∈ X–(V ∪ W) such that x≤t≤x). Since V and W are disjoint, the statement inside the parentheses is vacuously true.
Antisymmetry is clear, since x ≤’V, W y and y ≤’V, W x imply x≤y and y≤x, hence x=y.
For transitivity, let us assume x ≤’V, W y and y ≤’V, W z. Then x≤y and y≤z, so x≤z. Let us assume that x is in V and that z is in W. If y ∈ W, then by definition of x ≤’V, W y, there is a point t ∈ X–(V ∪ W) such that x≤t≤y, then x≤t≤z, so x ≤’V, W z. If y ∈ V, then by definition of y ≤’V, W z, there is a point t ∈ X–(V ∪ W) such that y≤t≤z, then x≤t≤z, so x ≤’V, W z. In the remaining case, y is in X–(V ∪ W), and x≤y≤z, so x ≤’V, W z.
2. We must show that the graph (≤’V, W) of ≤’V, W is closed in X × X. Let C be the (closed) complement of V and D be that of W. Let A be the collection of pairs (x, y) of points of X such that x≤t≤z for some t ∈ X–(V ∪ W), namely for some t ∈ C ⋂ D.
We claim that A is closed in X × X. To this end, let (x, y) be any point in the complement of A. For every t ∈ C ⋂ D, x≰t or t≰z, namely, (x, t) is outside (≤) or (t, z) is outside (≤). Since (≤) is closed, this means that there is an open rectangle Ut × Vt containing (x, t) and disjoint from (≤), or there is an open rectangle Vt × Wt containing (t, z) and disjoint from (≤). (I have intentionally chosen the same name Vt in each case. Please mind that Ut and Wt may not be defined for every t ∈ C ⋂ D, but at least one of them is.) The open subsets Vt cover C ⋂ D when t varies over C ⋂ D. Since C ⋂ D is closed in X, which is compact, C ⋂ D is itself compact. Therefore there is a finite subset E of C ⋂ D such that C ⋂ D ⊆ ∪u ∈ E Vu.
Let E1 be the subset of E consisting of those elements u such that (x, u) is outside (≤), in which case Uu is defined. We can form ∩u ∈ E1 Uu; since the intersection is finite, this is an open neighborhood of x. Let E2 ≝ E–E1: for every u ∈ E2, (x, u) is inside (≤) by definition of E1; since u ∈ E2 ⊆ E ⊆ C ⋂ D, it must then be that (u, y) is outside (≤), and therefore Wu is defined. We can now form ∩u ∈ E2 Wu; since the intersection is finite, this is an open neighborhood of y. Then ∩u ∈ E1 Uu × ∩u ∈ E2 Wu is an open neighborhood of (x, y) in X × X, and we claim that it is disjoint from A. Otherwise there would be a pair (x’, y’) ∈ ∩u ∈ E1 Uu × ∩u ∈ E2 Wu and a point t ∈ C ⋂ D such that (x’, t) ∈ (≤) and (t, y’) ∈ (≤). Since C ⋂ D ⊆ ∪u ∈ E Vu, t is in Vu for some u ∈ E. If u ∈ E1, then x’ ∈ Uu and t ∈ Vu, but Uu × Vu is disjoint from (≤) by construction, and this contradicts the fact that (x’, t) ∈ (≤). Hence u ∈ E2. But then, t ∈ Vu and y’ ∈ Wu, with Vu × Wu disjoint from (≤), and that is impossible since (t, y’) ∈ (≤). Hence, as promised, ∩u ∈ E1 Uu × ∩u ∈ E2 Wu is an open neighborhood of (x, y) that is disjoint from A. Since this holds for every pair (x, y) outside A, the complement of A is open, hence A is closed in X × X.
By definition, (≤’V, W) = (≤) ⋂ ((C × X) ∪ (X × D) ∪ A), a finite intersection of finite unions of closed subsets of X × X, hence it is itself closed in X × X.
3. Let us write ↓ for downward closure with respect to ≤ and ↓’ for downward closure with respect to ≤’V, W.
Let y be a local minimum of (X, ≤). There is an open neighborhood O of y in X such that O ⋂ ↓y = {y}. Every element ≤’V, W-below y is ≤-below y, so O ⋂ ↓’y ⊆ O ⋂ ↓y = {y}. Since y ∈ O, we conclude that O ⋂ ↓’y = {y}.
Conversely, let y be a local minimum of (X, ≤’V, W). We will use the fact that for every point x of X, x ≤’V, W y if and only if x≤y, provided that x ∉ V or y ∉ W (or that there is a point t between x and y, but we will not need that).
There is an open neighborhood O of y in X such that O ⋂ ↓’y = {y}. If y ∉ W, then for every point x of X, x ≤’V, W y if and only if x≤y, as we have just seen; so ↓’y=↓y, whence O ⋂ ↓y = {y}, and therefore y is a local minimum of (X, ≤). If y ∈ W, then O ⋂ W is also an open neighborhood of y. Now for every point x of W, x ∉ V since V and W are disjoint, so x ≤’V, W y if and only if x≤y; it follows that W ⋂ ↓’y = W ⋂ ↓y, so O ⋂ W ⋂ ↓y = O ⋂ W ⋂ ↓’y = W ⋂ {y} = {y}. Hence y is a local minimum of (X, ≤). ☐
Minimal closed partial orders with no local minimum in U
We wish to apply Lemma G iteratively as follows. We fix an open subset U of a compact pospace (X, ≤), containg no local minimum. If we can find two disjoint non-empty open subsets V and W such that ≤’V, W is strictly contained in ≤, namely such that there are points x ∈ V and y ∈ W with no point t between x and y outside V ∪ W, then we replace ≤ by ≤’V, W. We iterate this, possibly for transfinitely long, and eventually we obtain a minimal closed partial order with no local minimum in U. This minimal closed partial order will be order-dense (and slightly more), and we will be able to extract a maximal chain from it.
The transfinite iteration I have just hinted to, is really a transfinite sequence of choices (of pairs of open sets V and W), and making such a transfinite sequence of choices is exactly what Zorn’s Lemma does for us. In order to apply it, we have to show that a certain poset NLC(X) of closed partial orderings with no local minimum in U is an inductive poset, and we will prove below (Proposition I below) that it is even a dcpo.
The proof of Proposition I, which is exactly the proof given in Exercise VI-5.17 of [2], by the way, is pretty subtle. We start with an easy observation.
Lemma H. Let X be a space with a lower semiclosed ordering ≤, and Q be a compact subset of X. For every x ∈ Q, there is minimal element y ∈ Q with respect to ≤ such that y≤x.
Proof. We form the poset (Q, ≥), with the opposite ordering ≥, and we claim that it is an inductive poset. Let C be any chain of points of Q. The set of upper bounds (upper since we are considering the opposite ordering ≥) of C in Q is {y ∈ Q | ∀z ∈ C, y ≤ z} = ∩z ∈ C ↓z ⋂ Q, where ↓ is downward closure with respect to ≤. Since X is lower semiclosed, each set ↓z is closed in X. The set ∩z ∈ C ↓z is a filtered intersection of closed subsets of X that all intersect Q, hence it must also intersect Q (see Proposition 4.4.9 in the book); therefore the set of upper bounds of C is non-empty, showing that (Q, ≥) is an inductive poset. By Zorn’s Lemma, there is a maximal element above x in (Q, ≥), and this is the desired point y. ☐
Proposition I. Let X be a compact Hausdorff space, and U be an open subset of X. Let NLC(X) be the set of all partial orderings on X whose graph is closed in X × X and whose local minima do not belong to U. We order NLC(X) by reverse inclusion (of the graphs of the partial orderings). Then NLC(X) is a dcpo, and directed suprema are intersections (of graphs).
Proof. Let (≤i)i ∈ I be a directed family of elements of NLC(X), and ≤ be their intersection; more precisely, let ≤ be the relation whose graph (≤) is equal to ∩i ∈ I (≤i). It is clear that ≤ is a partial ordering, and since intersections of closed sets are closed, (≤) is closed in X × X.
It remains to show that no local minimum of ≤ belongs to U, and this is definitely the most inventive part. To start with, we will consider (≤i)i ∈ I as a monotone net (≤i)i ∈ I, ⊑, by defining ⊑ as: for all i, j ∈ I, i ⊑ j if and only if (≤i) ⊇ (≤j). We will only use this near the end of the proof.
Instead of proving that no local minimum of ≤ belongs to U, we will prove that, given any point x of U, x cannot be a local minimum of ≤. This is of course equivalent.
Let O be an open neighborhood of x. Our aim is to show that O ⋂ ↓x ≠ {x}, where ↓ denotes downward closure with respect to ≤. In other words, we aim to find a point z in O such that z≤x and z≠x.
Every compact Hausdorff space is locally compact (Proposition 4.8.8 in the book). Hence we can find two compact (saturated) subsets Q and Q’ such that x ∈ int(Q’) ⊆ Q’ ⊆ int(Q) ⊆ Q ⊆ U ⋂ O. We find Q’ by relying on local compactness, then Q by the interpolation property for locally compact spaces (Proposition 4.8.14 in the book).
The plan is to find a point zi in Q–int(Q’) such that zi ≤i x for every i ∈ I; then, since Q–int(Q’) is compact, (zi)i ∈ I, ⊑ will have a subnet that converges to a point in Q–int(Q’), and that will be our desired point z. Showing that z ∈ O will be easy, since z ∈ Q–int(Q’) ⊆ O; showing that z ≤ x will involve showing that z ≤i x for every i ∈ I, and that will follow from the definition of z, the fact that each ≤i is semiclosed (we will return to that at the end of the proof); finally, the fact that z is not in int(Q’) will ensure that z≠x.
We find the point zi in the following clever way. For each i ∈ I, there is a point yi in Q’ that is minimal with respect to ≤i and such that yi ≤i x by Lemma H. (This lemma applies because, since (≤i) is closed, ≤ is in particular semiclosed, hence lower semiclosed; see the “arc chains” section in the January 2025 post.) Since yi ∈ Q’ ⊆ U, yi is not a local minimum of ≤i for any i ∈ I. Namely, for every open neighborhood O of yi in X, O ⋂ ↓iyi ≠ {yi}. We apply this to O ≝ int(Q), and we find that there must be a point zi≠yi in int(Q) ⋂ ↓iyi. In other words, zi <i yi and zi ∈ int(Q). Since yi is minimal with respect to ≤i in Q’, zi <i yi implies that zi cannot be in Q’. Therefore zi ∈ int(Q)–Q’.
We recall that int(Q’) ⊆ Q’ ⊆ int(Q) ⊆ Q, so zi is in the larger set Q–int(Q’). The set Q–int(Q’) is the intersection of the compact set Q with the complement of int(Q’). Any intersection of a compact set with a closed set is compact (Corollary 4.4.10 in the book), so Q–int(Q’) is compact. We consider the net (zi)i ∈ I, ⊑; the preordering ⊑ on I was introduced near the beginning of the proof, by i ⊑ j if and only if (≤i) ⊇ (≤j). The net (zi)i ∈ I, ⊑ is a net of points in the compact set Q–int(Q’), so it has a subnet (zα(j))j ∈ J, ⪯ that converges to some point z ∈ Q–int(Q’) (Corollary 4.7.27 in the book).
We claim that, for every i ∈ I, z ≤i x. In order to see this, let ↓i be downward closure with respect to ≤i. Since (≤i) is closed in X × X, ≤i is in particular semiclosed hence lower semiclosed. Therefore ↓ix is closed in X. If z ≰i x, then z would be in the open complement of ↓ix, so zα(j) would be in that same complement for j ∈ J large enough; in other words, there would be an index j ∈ J such that for every j’ ∈ J such that j ⪯ j’, zα(j’) ≰i x. By definition of a subnet, there is an index j’ ∈ J such that i ⊑ α(j’), and we can choose it so that j ⪯ j’ since J is directed under ⪯. Therefore zα(j’) ≰i x. Now that i ⊑ α(j’), by definition of ⊑, we have (≤i) ⊇ (≤α(j’)). But zα(j’) <α(j’) yα(j’) ≤α(j’) x, so zα(j’) ≤α(j’) x, and (≤i) ⊇ (≤α(j’)) then entails that zα(j’) ≤i x, which contradicts zα(j’) ≰i x.
We have shown that for every i ∈ I, z ≤i x. Therefore z ≤ x. Since x ∈ int(Q’) and z ∈ Q–int(Q’), we must have z≠x. Let us recapitulate. We have found a point z ∈ Q–int(Q’) such that z≤x and z≠x. Since Q–int(Q’) ⊆ Q ⊆ O, z is in O. Therefore z is in O ⋂ ↓x and not in {x}, showing that O ⋂ ↓x ≠ {x}. Since O is an arbitrary open neighborhood if x, x is not a local minimum of ≤. Since x is an arbitrary point in U, no point of U is a local minimum of ≤, equivalently no local minimum of ≤ is in U. ☐
The proof of Koch’s arc theorem.
We start with the assumptions of Koch’s arc theorem: (X, ≤) is a pospace, U is an open subset of X whose closure is compact and that does not contain any local minimum of ≤, and x is a point of U.
Let me restate an argument we made in Remark A. In the situation described above, cl(U) is a compact subspace of X, and the restriction of ≤ to cl(U) is still closed; namely, (≤) ⋂ (cl(U) × cl(U)) is closed in cl(U) × cl(U). We will show that given any point x of U, there is an arc chain from a point of ∂U to x in the subspace cl(U). This will clearly be an arc chain in X from a point of ∂U to x in X that is contained in cl(U). Hence, replacing X by cl(U) if necessary, we will assume that X itself is compact, and that cl(U)=X, namely that U is dense in X.
By Proposition I, NLC(X) is a dcpo under reverse inclusion. Hence it is an inductive poset, and since ≤ is an element of NLC(X), Zorn’s Lemma tells us that there is an element ≤min of NLC(X) above ≤ (with respect to reverse inclusion). In other words, there is a minimal (with respect to inclusion) closed partial ordering ≤min on X such that (≤min) ⊆ (≤) and whose local minima are all outside U.
For every pair of disjoint open subset V and W of X, the partial ordering ≤min‘V,W defined and studied in Lemma G is another element of NLC(X), and lies above it in the reverse inclusion ordering; namely, its graph is included in that of ≤min. Since the latter is minimal, ≤min‘V,W = ≤min. In other words, expanding out the definition of ≤min‘V,W:
Fact J. For every pair of disjoint open neighborhoods V and W, for every y ∈ V, for every z ∈ W, there is point t ∈ X–(V ∪ W) such that y ≤min t ≤min z.
Remember that we have fixed a point x in U. Let P be the downward closure of x with respect to ≤min. We use Hausdorff’s maximality theorem and we produce a maximal chain C in P. That was our original idea for proving Koch’s arc theorem, but beware that P is now a maximal chain with respect to the minimal ordering ≤min, not ≤.
Claim K. (X, ≤min) is order-dense, and so is (C, ≤). If C contains at least two elements, then C is an arc chain.
Proof. Let y ≤min z with y≠z. Since X is Hausdorff, there are two disjoint open neighborhoods V of y and W of z. By Fact J, there is point t ∈ X–(V ∪ W) such that y ≤min t ≤min z. Since t is neither in V nor in W, t is distinct from both x and y. Hence (X, ≤min) is order-dense.
In order to see that (C, ≤) is order-dense, too, we consider any two points y and z of C such that y<z. In general, y<z does not imply y <min z, but this is true if both are in C, because C is totally ordered by ≤min: if y <min z failed, then we would have z ≤min y, and since (≤min) ⊆ (≤), this would entail z≤y, contradicting y<z. Hence y <min z. Since (X, ≤min) is order-dense, there is a point t in X such that y <min t <min z.
This point t may fail to be in C, but C is a maximal chain with respect to ≤min. Hence, if no point u of C were strictly between y and z with respect to ≤min, namely if all points of C were either ≤min y or ≥min z (using the totality of ≤min on C), then C ∪ {t} would be a strictly larger chain, which is impossible. Hence there is a point u of C such that y <min u <min z. Since (≤min) ⊆ (≤), it follows that y < u < z.
We now know that C is an order-dense chain. It is an order-dense chain in a compact pospace (hence a compact space with a semiclosed partial ordering), so Proposition F allows us to say that C is an arc chain… provided that C contains at least two elements. We don’t know that yet, and this is why this is left as an assumption in Claim K; but we will prove it below. ☐
Our final claim below, and particular the fact that the least element of C is in ∂U, is the only place in the whole proof where we use the fact that U does not contain any local minimum. The assumptions of Koch’s arc theorem are that U does not contain any local minimum of the original ordering ≤, Proposition I allowed us to refine ≤ into a closed partial ordering ≤min such that U does not contain any local minimum of ≤min, and Claim L below is the place where we (finally!) use the latter property.
Claim L. The largest element of C is x. The least element of C is in ∂U. In particular, C contains at least two elements.
Proof. Let me recall that C is a maximal chain inside P, the downward closure of x with respect to ≤min. Both C and P are ordered by ≤min. If C did not contain x, then C ∪ {x} would be a strictly larger chain, contradicting maximality. Hence x ∈ C, and therefore x is the largest element of C.
Since (≤min) is closed, ≤min is semiclosed, so P, which is the downward closure of x with respect to ≤min, is closed in X. Since (X, ≤min) is a pospace, it follows that (P, ≤min)—or rather, P with the restriction of ≤min to P—is a pospace. Since X is compact, P is compact, too, because P is closed. Lemma C states that every maximal chain in a pospace is closed. Hence C is closed, hence compact in P. It is non-empty, since it is a chain (or since it contains x).
By Lemma A of the January 2025 post, every non-empty compact space with a semiclosed total ordering is a complete lattice. Hence C is a complete lattice, and therefore has a least element a. We observe that a is a minimal element of (X, ≤min): if not, there would be a point x <min a, and then C ∪ {x} would be a strictly larger chain than C, contradicting the maximality of C.
If a were in U, then U would intersect the downward closure ↓mina of a with respect to ≤min at a, and at a only: otherwise there would be another point in the intersection, and that point would necessarily be strictly smaller than a with respect ≤min, which is impossible since a is ≤min-minimal. In other words, if a were in U, then it would be a local minimum of ≤min, and in U. This is impossible, since ≤min is in NLC(X) and (look back at Proposition I) we have defined NLC(X) as a collection of closed partial orderings that have no local minimum in U. We must conclude that a is not in U, hence that a is in X–U. But ∂U = cl(U)–U (since U is open) = X–U (since U is dense in X, namely cl(U)=X). Therefore a is in ∂U.
Finally, C contains at least two elements, because a≠x. Indeed x is in U, while a is in ∂U = X–U. ☐
Let us summarize what we have obtained. Given a compact pospace (X, ≤), a dense open subset U of X that contains no local minimum of ≤, we have built a chain C ⊆ X that has at least two elements (Claim L). The last part of Claim K tells us that C is an arc chain, and Claim L tells us that it is an arc chain from a point of ∂U to x. By Remark A (which I have restated at the beginning of this section), this finishes the proof of Koch’s arc theorem.
- Robert Jacob Koch. Arcs in partially ordered spaces. Pacific Journal of Mathematics 9:723–728, 1959.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Jimmie Lawson. Chains in partially ordered spaces. Topology Proceedings 61:123–137, 2023.

— Jean Goubault-Larrecq (March 20th, 2025)
