On products of dcpos, the Miao-Xi-Li-Zhao lemma, and the complete lattice Lfan (part I)

Given a poset P, we can form the space P_σ obtained by giving P the Scott topology. Now we can form two products, either by forming the poset product of P with itself, and then taking the Scott topology, yielding (P × P)_σ, or taking the Scott topology first, and then building the topological product P_σ × P_σ (namely, with the product topology, generated by open rectangles).

The (Scott) topology of (P × P)_σ is always finer than that of P_σ × P_σ, and is often identical, for example if P is a continuous poset (Proposition 5.1.54 in the book); but also, more generally, if P_σ is core-compact; or if P_σ is first-countable. The latter are points 1(a) and 1(b) from this post, where I discussed the Chen-Kou-Lyu property [1]: P has the Chen-Kou-Lyu property if and only if the Scott topology on the product Pⁿ of P with itself n times (with n an arbitrary natural number) coincides with the product of the Scott topologies.

I would like to state another result of this kind, due to Hualin Miao, Xiaoyong Xi, Qingguo Li, and Dongsheng Zhao [2, Lemma 3.1]. But this is really an excuse: my initial intention was to talk about a funny dcpo that has the Chen-Kou-Lyu property, but is neither core-compact nor first-countable in its Scott topology; and showing that it has the Chen-Kou-Lyu is best obtained as a consequence of the Miao-Xi-Li-Zhao result.

This funny dcpo is very simple, and I will explore its many properties this month and next month. Doing it in just one post would be too much. I will not say what it is right away: you will have to wait until after the statement and proof of the Miao-Xi-Li-Zhao Lemma! But let me say for now that it seems to have been rediscovered many times. The first occurrence I know of it is due to Xu, Shen, Xi and Zhao [3, Example 4.8] in 2020. Then it was rediscovered independently by Chen, Kou and Lyu [1, Example 4.9] and by Hertling [4, Example 4.7] in 2022.

The Miao-Xi-Li-Zhao Lemma

The Miao-Xi-Li-Zhao lemma states that, given two posets P and Q which only have countably many ideals, then (P × Q)_σ = P_σ × Q_σ. The proof shows that we can weaken the assumptions somehow. Let us say that a directed family D is trivial if and only if it has a largest element, and non-trivial otherwise. The trivial directed families are uninteresting when studying the Scott topology: a subset U of a poset is Scott-open if and only if it is upwards-closed and it intersects every non-trivial directed family D whose supremum sup D exists and is in U; indeed, if D is a trivial directed family and sup D is in U, then D intersects U, whatever U may be.

An ideal is a downwards-closed directed subset, and it is non-trivial if and only if it is non-trivial as a directed subset; equivalently, if and only if it is not of the form ↓x for any point x.

We will not assume that there are countably many ideals, or even countably many ideals that have suprema, but just that the family of non-trivial ideals that have suprema is countable. This is a tiny improvement over what Miao, Xi, Li and Zhao stated, but a proper improvement nonetheless: given a poset P with countably many non-trivial ideals that have suprema, adding uncountably many pairwise incomparable points, all incomparable to all the points of P, to P, yields a poset that still only has countably many non-trivial-ideals-that-have-suprema, but uncountably many ideals.

Theorem A (Miao, Xi, Li, Zhao). Let P and Q be two posets. If both P and Q only have countably many non-trivial ideals that have suprema, then (P × Q)_σ = P_σ × Q_σ.

Proof. Let me call a (directed) sup situation on P, for short, any non-trivial ideal I that has a supremum; and similarly in Q. Let me say that a subset U of P (resp., Q) respects a sup situation I if and only if sup I ∈ U implies I intersects U; in other words, if and only if sup I is not in U or I intersects U. These denominations are inspired by very similar notions used in the Rasiowa-Sikorski and Görnemann-Rauszer-Sabalski lemmas, which I have talked about in this post in December 2019. But the sup situations there were not directed, so there are some differences; and we will not need any form of the Baire property to conclude.

I claim that U is Scott-open if and only if it is upwards-closed and respects every sup situation. The only if direction is clear. In the if direction, let us consider any directed family D with a supremum x in U. Then ↓D is an ideal, with supremum x. If x is in ↓D, then x≤y for some y ∈ D, and since x is in U and U is upwards-closed, y is in D and in U, so D intersects U. Otherwise, ↓D is a non-trivial ideal, hence a sup situation. By assumption, U respect ↓D, so ↓D intersects U, and since U is upwards-closed, D must intersect U as well.

The key observation we will use to show the theorem is the following:

Claim. Let W be a Scott-open subset of P × Q, I₀, …, I_n–1, I_n be finitely many sup situations on P, and A and B be two non-empty finite subsets of P and Q respectively such that A × B ⊆ W, and such that ↑A respects the sup situations I₀, …, I_n–1. Then there is a finite subset A’ of P containing A such that A’ × B ⊆ W, and such that ↑A’ respects the sup situations I₀, …, I_n–1 and also I_n.

Proof of the claim. For short, let x_k denote the supremum of I_k, for each k with 0≤k≤n. If the supremum x_n of I_n is not in ↑A, then we simply take A’ ≝ A. Then A’ × B ⊆ W, trivially, ↑A’ = ↑A respects the sup situations I₀, …, I_n–1, trivially as well, and also respects the sup situation I_n because x_n is not in ↑A. Hence, we will assume that x_n is in ↑A from now on. The situation is as in the figure below. The dotted, squiggly lines below each point x_k are meant to denote I_k; ↑A (in orange) respects each of the corresponding sup situations: e.g., x₀ and x₁ are not even in ↑A, while x_m–1, x_m, …, x_n–1 and in ↑A, and some points in the dotted lines below them are in ↑A, too. For x_n, we have assumed that it is in ↑A, but we don’t know whether any point from the dotted line I_n below it is also in ↑A.

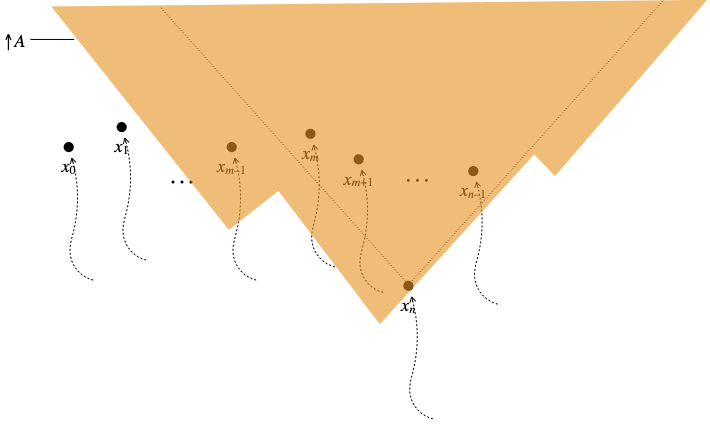
Among x₀, …, x_n–1, some elements may be larger than or equal to x_n, some may not. Up to a permutation of indices, we will assume that x₀, …, x_m–1 are those elements that are not larger than or equal to x_n, while x_m, …, x_n–1 are larger than or equal to x_n. This is the situation shown above: x_m, …, x_n–1 are the points in the cone of points above x_n, materialized by the two slanted, dotted lines originating from x_n and going up and sideways.

Let C be ↓{x₀, …, x_m–1}. This is a Scott-closed subset of P which does not contain x_n. We represent it in blue below.

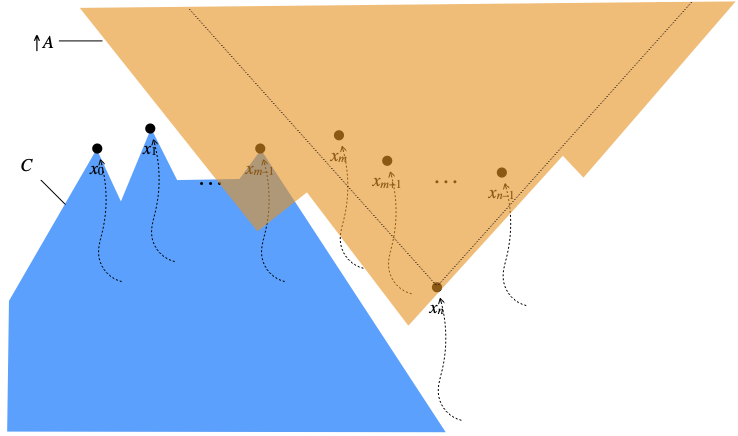
Since C is closed, its complement U is a Scott-open neighborhood of x_n. For each index k with m≤k≤n, we have x_k≥x_n, so x_k is in U as well. (This should be particularly obvious from the picture.) We will build a point x’_k, one for each index k with m≤k≤n, as follows.

• The point x_k is larger than or equal to some point a of A. Indeed, when k=n, this is because x_n is in ↑A, and if m≤k<n, this is because x_k≥x_n and x_n is in ↑A. For each one of the finitely many elements b of B, (a, b) is then in A × B, hence in W. Therefore (x_k, b) is in W, since W is upwards-closed. We have observed that x_k is in U, so (x_k, b) is in W ∩ (U × Q), and that intersection is Scott-open.
• For each b ∈ B, the pair (x_k, b) is the supremum of the directed family of points (x’, b) where x’ ranges over I_k, so since W ∩ (U × Q) is Scott-open, we can find a point in I_k—which we will write as x’_k,b to show its dependency on both k and b—such that (x’_k,b, b) ∈ W ∩ (U × Q). Said otherwise, x’_k,b is in I_k and in U, and (x’_k,b, b) ∈ W.
• Since I_k is directed and B is finite, there is a point x’_k in I_k that is larger than or equal to x’_k,b for every b ∈ B. Since U and W are upwards-closed, we obtain that x’_k is in U, and that (x’_k, b) ∈ W for every b ∈ B.

Here is the situation now. We have highlighted the new points x’_m, …, x’_n. Since they are all in U, we have shown them outside the blue box C.

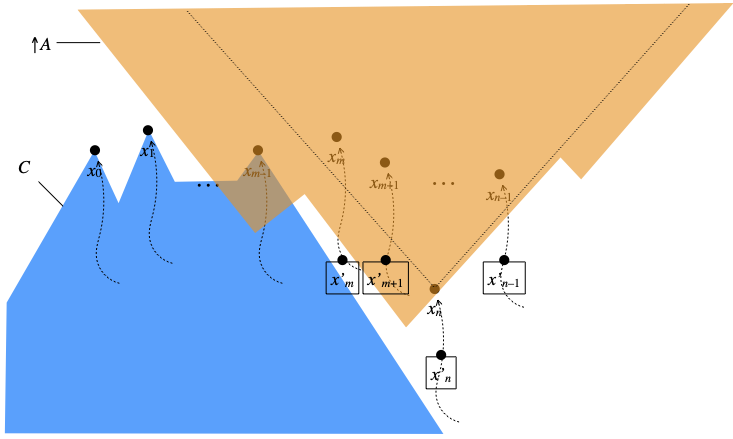
We now define A’ as A ∪ {x’_m, …, x’_n}. It is easy to see that A’ × B ⊆ W, because A × B ⊆ W and (x’_k, b) ∈ W for every b ∈ B. Let us check that ↑A’ respects the sup situations I₀, …, I_n–1 and I_n. We check that it respects the sup situations I_j with 0≤j<m first, then those I_k with m≤k≤n.

• For every j with 0≤j<m, if x_j is in ↑A’, then we claim that x_j is in fact in ↑A. Otherwise, we would have x_j≥x’_k for some k such that m≤k≤n; but x_j is in the Scott-closed set C, by definition of the latter, so x’_k would be in C as well, and that is impossible since x’_k is in U; we recall that U is the complement of C. Hence x_j is in ↑A. Since ↑A respects the sup situation I_j, some element of I_j is in ↑A, hence in ↑A’. Therefore ↑A’ respects the sup situation I_j.
• For every k with m≤k≤n, in order to show that ↑A’ respects the sup situation I_k, we need to show that if x_k is in ↑A’ (which happens to be true, but this will not matter), then ↑A’ contains some element of I_k. And indeed ↑A’ contains some element of I_k, namely x’_k. (End of proof of Claim.)

By exchanging the roles of P and Q, we have the following.

Dual Claim. Let W be a Scott-open subset of P × Q, J₀, …, J_n–1, J_n be finitely many sup situations on Q, and A and B be two non-empty finite subsets of P and Q respectively such that A × B ⊆ W, and such that ↑B respects the sup situations J₀, …, J_n–1. Then there is a finite subset B’ of Q containing B such that A × B’ ⊆ W, and such that ↑B’ respects the sup situations J₀, …, J_n–1 and J_n.

With the help of the Claim and of the Dual Claim, we can now prove the Theorem.

Every open subset of P_σ × Q_σ is Scott-open in P × Q, namely open in (P × Q)_σ, so we concentrate on the converse statement. Let us fix a point (x, y) in P × Q, and W be a Scott-open neighborhood of (x, y) in P × Q. We wish to show that W contains an open rectangle U × V, where U is a Scott-open neighborhood of x in P and V is a Scott-open neighborhood of y in Q. Once we have managed to do so, and making (x, y) vary inside W, we will have obtained that W is an open neighborhood of any of its elements in P_σ × Q_σ, hence is open in P_σ × Q_σ, and the proof will be complete.

We start with the case where both P and Q have at least one sup situation. (There is a formal catch when there is no sup situation at all). Then we can enumerate the sup situations of P as I_n, n ∈ N, and the sup situations of Q as J_n, n ∈ N, possibly repeating some sup situations. For example, if P has just three sup situations I₀, I₁ and I₂, we can simply decide to define I₃, I₄, …, as all being equal to I₂. But we cannot do that if P has no sup situation at all, whence the ‘formal catch’. (I apologize for being so formal.)

Right, anyway, assuming that both P and Q have at least one sup situation, we define sequences A₀ ⊆ A₁ ⊆ … ⊆ A_n ⊆ … and B₀ ⊆ B₁ ⊆ … ⊆ B_n ⊆ … of finite subsets of P and Q respectively in such a way that:

1. each A_n contains x,
2. each B_n contains y,
3. ↑A_n respects the sup situations I₀, …, I_n–1,
4. ↑B_n respects the sup situations J₀, …, J_n–1, and
5. A_n × B_n ⊆ W.

We initialize A₀ to {x} and B₀ to {y}. Then, for every natural number n≥1, we apply the Claim to A ≝ A_n–1 and B ≝ B_n–1; this yields a finite subset A’ of P, and we define A_n ≝ A’. Then we apply the Dual Claim that A ≝ A_n and B ≝ B_n–1; this yields a finite subset B’ of Q, and we define B_n ≝ B’.

If instead P has at least one sup situation and Q has none, then we only use the Claim to define A_n ≝ A’ as above, and we let B_n ≝ B_n–1 at each step; in that case, we guarantee conditions 1, 2, 3 and 5, but not 4, which would be meaningless. The situation is symmetric if Q has at least one sup situation and P has none. If neither P nor Q has a sup situation, we simply define A_n as {x} and B_n as {y} for every natural number n.

In any case, once the sequences A₀ ⊆ A₁ ⊆ … ⊆ A_n ⊆ … and B₀ ⊆ B₁ ⊆ … ⊆ B_n ⊆ … have been built, we define A as the union of the sets A_n, n ∈ N, and U as ↑A, while we define B as the union of the sets B_n, n ∈ N, and V as ↑B. By construction, U respects all the sup situations of P, V respects all the sup situations of Q, so they are Scott-open in P and in Q respectively. Condition 5 above guarantees that U × V ⊆ W, while conditions 1 and 2 ensure that U × V contains (x, y).

And that’s it: we have found the two Scott-open neighborhoods U of x and V of y such that U × V ⊆ W, as promised. We have argued earlier why this was enough to conclude that W is open in P_σ × Q_σ. ☐

The complete lattice L_fan

I started this month’s post by saying that I would present an example of a dcpo L_fan that has the Chen-Kou-Lyu property, because of the just mentioned Miao-Xi-Li-Zhao result, although (L_fan)_σ is neither core-compact nor first-countable. Here it is at last.

L_fan is simply N × N, with equality as ordering on the first component and the usual ordering on the second component, plus an extra bottom element ⊥, plus an extra top element ⊤:

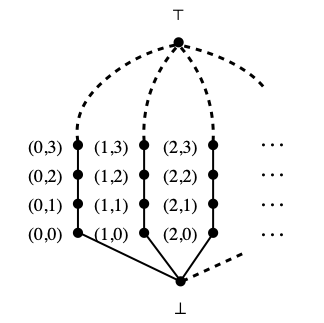
Formally, the elements of L_fan are ⊥, ⊤ and all pairs (m, n) of natural numbers, ordered by x≤y if and only if x=⊥, or y=⊤, or x is a pair (m, n) and y is a pair (m’, n’) with m=m’ and n≤n’. In the sequel, I will call the set of pairs whose first element is equal to m a column, and precisely, column number m.

As I have already said, the first occurrence I know of it is due to Xu, Shen, Xi and Zhao [3, Example 4.8] in 2020. Then it was rediscovered independently by Chen, Kou and Lyu [1, Example 4.9] and by Hertling [4, Example 4.7] in 2022.

I have decided to call it L_fan because what remains when you remove the bottom element ⊥ is very close to the sequential fan; just like it, it will be countable but not first-countable.

L_fan has the Chen-Kou-Lyu property

Hertling showed that L_fan has the property that the product of the Scott topology is the Scott topology of the product, namely (L_fan × L_fan)_σ = (L_fan)_σ × (L_fan)_σ [4, Lemma 4.12]. Hertling’s proof is a bit long and technical… but this is an immediate consequence of the Miao-Xi-Li-Zhao lemma. Indeed, L_fan only has countably many non-trivial ideals, and those are its columns (with ⊥ added). Since L_fan is countable, it even has countably many ideals, trivial or not.

A poset P has the Chen-Kou-Lyu property if and only if, for every natural number n, the n-fold product of P with itself is the same whether with the Scott topology of the poset product, or with the product topology of the Scott topologies. In order to see that L_fan has the Chen-Kou-Lyu property, we need to observe the following: the ideals of any finite product of posets are the products of ideals. You can check it by hand if you will. Here is a hammer of an argument:

• The irreducible closed subsets of a product of spaces are the products of irreducible closed subsets of each space (Proposition 8.4.7 in the book).
• But the ideals of a poset P are exactly the irreducible closed subsets of P_a, where P_a is P with the Alexandroff topology (Fact 8.2.49 in the book), and the Alexandroff topology of a finite product of posets is the product topology of the Alexandroff topologies (Exercise 4.5.19 in the book).

Knowing this, the nth power (L_fan)ⁿ of L_fan (as a poset) has only countably many ideals, since it has exactly as many as there are n-tuples of ideals of L_fan, and L_fan only has countably many ideals. Therefore, by Theorem A (the Miao-Xi-Li-Zhao lemma) and an easy induction on n, ((L_fan)ⁿ)_σ = ((L_fan)_σ)ⁿ: this is clear if n=0, and otherwise ((L_fan)ⁿ)_σ = (L_fan)_σ × ((L_fan)^n–1)_σ (by Theorem L, since both L_fan and (L_fan)^n–1 have countably many ideals) = (L_fan)_σ × ((L_fan)_σ)^n–1 (by induction hypothesis) = ((L_fan)_σ)ⁿ. Therefore, as promised:

Proposition B. L_fan has the Chen-Kou-Lyu property.

As a consequence, and in passing, we can then use the argument in Section ‘The Chen-Kou-Lyu property’ of this post (March 2022):

Corollary C.  The Scott topology coincides with the lower Vietoris topology on H((L_fan)_σ).

Basic properties of L_fan

Let me list some of the basic properties of L_fan; we will see the others next month.

Lemma D. L_fan is a complete lattice.

Proof. The supremum of any subset A that contains ⊤, or two elements from different columns, or elements (m, n) from the same column m but with arbitrarily large n, is ⊤. The supremum of the empty set, the supremum of {⊥}, is ⊥. All other subsets of L_fan consist of pairs (m, n) with the same m, with n bounded, and at least one such pair (plus possibly ⊥), and their supremum is the point (m, n) with the largest value of n. Infima can be described similarly. ☐

Let us investigate the Scott topology on L_fan. For every function f : N → N, let U_f be the subset of those pairs (m, n) of N × N such that n≥f(m), plus ⊤.

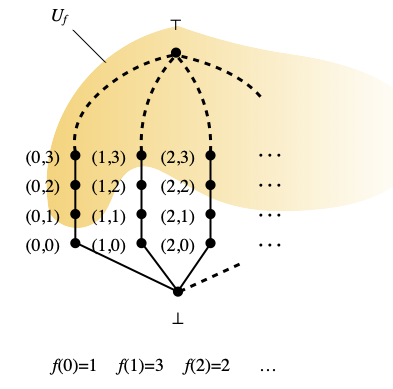
Lemma E. The Scott-open subsets of L_fan are exactly the sets U_f, where f ranges over the functions from N to N, plus the empty set, plus the whole space L_fan.

Proof. A Scott-open subset U is any upwards-closed subset such that every non-trivial directed family D whose supremum is in U already contains an element that is in U. A non-trivial directed family D must be infinite. In particular, in L_fan, every non-trivial directed family D must contain infinitely many elements different from ⊥ and from ⊤. If any two (say x and y) are in two different columns, then D must contain a larger element than both x and y, and that can only be ⊤, which would entail that D is trivial. Hence D (minus ⊥, whereas ⊤ cannot be in D) must be entirely included in a single column, say column m. Additionally, since D is non-trivial, the elements in that column must be equal to (m, n) with n arbitrarily high. Therefore sup D=⊤.

We use this to show that U_f is Scott-open. It is clearly upwards-closed. We consider any non-trivial directed family D as above. We do not need to require that sup D be in U_f, because sup D=⊤, which is in U_f anyway. D contains pairs (m, n) where m is fixed and n can be made as large as we wish; in particular, such that n≥f(m), and then the pair (m, n) is in D and in U_f.

Conversely, let U be a non-empty, proper Scott-open set. (“Proper” means different from the whole space.) Since U is non-empty, and upwards-closed, it contains ⊤. For every natural number m, the directed family {(m, n) | n ∈ N} has ⊤ as supremum, which is in U, so (m, n) is in U for some n ∈ N. We pick the smallest possible n, and we call it f(m). This defines a function f from N to N, and since U is upwards-closed, the elements of U are exactly ⊤ plus all the pairs (m, n) with m arbitrary and n≥f(m). Therefore U=U_f. ☐

The following is easy to see, too:

Fact F. For any two functions f, g : N → N, U_f ⊆ U_g if and only if f≥g, namely if and only if f(m)≥g(m) for every m ∈ N.

Hence:

Proposition G. The lattice O(L_fan) of Scott-open subsets of L_fan is order-isomorphic to the lattice M obtained by adding a top and a bottom element to the poset (N → N)^op of functions from N to N, ordered with the opposite ordering ≥ (not ≤).

M is the letter used by Chen, Kou and Lyu [1, Example 4.13].

Some nasty things about L_fan

We had promised that L_fan would neither be first-countable nor core-compact in its Scott topology, and this is now pretty easy.

Proposition H. L_fan is not first-countable in its Scott topology.

Proof. It suffices to show that ⊤ does not have a countable base of Scott-open neighborhoods. If it has, by Lemma E, there would be countably many functions f_k, k ∈ N, such that every open neighborhood of ⊤ of the form U_f contains U_fk for some k ∈ N. In other words, using Fact F, every function f from N to N would have to be smaller than or equal to some f_k. But this impossible: the function f that maps every k ∈ N to f_k(k)+1 cannot be smaller than or equal to any f_k, since that would imply f(k)=f_k(k)+1 ≤ f_k(k). This is a classical instance of a diagonal argument. ☐

One can see that L_fan is not a continuous dcpo: no pair (m, n) is way-below any element, since {(m+1, j) | j ∈ N} is a directed family whose supremum (⊤) is above (m, n), but no element (m+1, j) is above (m, n). The top element ⊤ is not way-below anything either, and in fact the way-below relation on L_fan is given by x ≪ y if and only if x=⊥.

The situation is much worse than that: in its Scott topology, L_fan is not locally compact, and even more generally, we have the following.

Proposition I. L_fan is not core-compact in its Scott topology.

Proof. We use the definition (Definition 5.2.3 in the book), and we show that the lattice of Scott-open subsets O(L_fan) of L_fan is not a continuous dcpo. By Proposition G, it suffices to show that M = (N → N)^op ∪ {⊥, ⊤} is not continuous.

Let f, g be any element of (N → N)^op, and let us imagine that f is way-below g in M. In particular, f is below g, namely f≥g (remember: we use the opposite ordering ≥). For every n ∈ N, let f_n : N → N map every m<n to g(m), and every m≥n to f(m)+1. The supremum of the maps f_n as n varies, namely its pointwise infimum, is g. But no f_n is above f, namely there is no natural number n such that f_n≤f ; indeed, applying both sides to n, we have f_n(n)=f(n)+1 ≰ f(n).

That is enough to conclude that M is not continuous: the only element way below an element g of (N → N)^op in M is ⊥, and the supremum of that lone element is not g. ☐

Hertling proves the same thing by showing that (∈) ≝ {(x, U) | x ∈ U ∈ O(L_fan)} is not open in the product topology [4, Lemma 4.10]. This is equivalent, because (∈) is open in the product topology if and only if the space is core-compact (Exercise 5.2.7 in the book), but I believe the proof above is simpler.

Let me stop here for this month. We will see additional nice and nasty properties that L_fan enjoys next month.

1. Yu Chen, Hui Kou, and Zhenchao Lyu.  Two topologies on the lattice of Scott closed subsets.  Topology and its Applications, 306, 107918, 2022.
2. Hualin Miao, Xiaoyong Xi, Qingguo Li, and Dongsheng Zhao. Not every countable complete distributive lattice is sober, Mathematical Structures in Computer Science 33(9):809–831, October 2023. arXiv version arXiv:2205.00250v1 [math.GN], 30 Apr 2022.
3. Xiaoquan Xu, Chong Shen, Xiaoyong Xi, and Dongsheng Zhao. First countability, ω-well-filtered spaces and reflections.  Topology and its Applications, 279, 107255, 2020.
4. Peter Hertling.  Topological properties of the binary supremum function. Semigroup Forum 104:618–646, 2022.
5. Klaus Keimel and Jimmie Lawson. Measure extension theorems for T₀-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
6. Douglas N. Hoover.  Maximal Limit Spaces, Powerspaces, and Scott Domains.  Proceedings of the 11th International Conference on Mathematical Foundations of Programming Semantics (MFPS), New Orleans, Louisiana, USA. Electronic Notes in Theoretical Computer Science 1:253–272, 1995.
7. Reinhold Heckmann. An upper power domain construction in terms of strongly compact sets. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds) Mathematical Foundations of Programming Semantics. MFPS 1991. Lecture Notes in Computer Science, vol 598. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-55511-0_14
8. Andrea Schalk. Algebras for Generalized Power Constructions. PhD Thesis, TU Darmstadt, 1993.
9. Xiaoquan Xu and Zhongqiang Yang.  Coincidence of the upper Vietoris topology and the Scott topology.  Topology and its Applications 288, February 2021.

— Jean Goubault-Larrecq (May 20th, 2024)