Let me return to a topic that I have addressed a few times in recent posts: under which conditions does the Scott topology of the product of two posets coincide with the product topology of the Scott topologies? In other words, when does the equation (P × Q)σ = Pσ × Qσ hold? Until now, I had presented four cases:
- when P and Q are continuous posets (Proposition 5.1.54 in the book), but this is subsumed by the next case;
- when Pσ or Qσ are core-compact, see the Proposition after item 1(a) in the post of March 20th, 2022;
- when Pσ and Qσ are first-countable, see the post of May 20th, 2019;
- when both P and Q only have countably many non-trivial ideals with existing suprema; this is the Miao-Xi-Li-Zhao lemma [1], and was the first thing I dealt with in this post of May 20th, 2024.
Jimmie Lawson and Xiaoquan Xu recently published a paper with an interesting idea in it [2], and give a new case where (P × Q)σ = Pσ × Qσ. They call their new class of posets with that property lcω-posets, a special case of a notion they also introduce and which they call lcω-spaces. As we will see, the whole proof that (P × Q)σ = Pσ × Qσ for lcω-posets P and Q revolves around colimits in Top, which products distribute over colimits in Top, and how colimits in Top and in the category of posets and Scott-continuous maps compare.
This is the sequel to last month’s post, where I explored the cases where products distribute over colimits in Top in detail. The only thing to remember from that post is that (basically the only case where) they do distribute is in the case of what I called ω-rigid colimits of core-compact spaces. But I’ll say that again later below.
Topologies determined by families of spaces and subdcpos
Let X be a topological space, and F be a family of subspaces of X. Hence every subspace K in the family F has the subspace topology, and this means that for every open subset U of X, U ∩ K is open in K for every K ∈ F.
The topology of X is determined by the subspaces in F if and only if the converse holds: every subset U of X such that U ∩ K is open in K for every K ∈ F is open in X. This is how compactly generated Hausdorff spaces are usually defined, for example: as Hausdorff spaces whose topology is determined by the family of its compact subspaces.
Let us relax the condition a bit, and drop the requirement that F be a family of subspaces. Instead, we require that each member of F be a subset K of X, with a topology τ that may or may not be the subspace topology. Explicitly, if F is a family of topological spaces (K, τ) where each K is a subset of X, we will say that the topology of X is determined by F if and only if for every subset U of X, U is open in X if and only if U ∩ K is open in (K, τ) for every (K, τ) ∈ F.
As we will see, Lawson and Xu are particularly interested in the case where F is a (countable) family of subdcpos K of a dcpo X (more generally, a sub-d-poset, but let us not make things too complicated for now), and the topology τ associated with K is the Scott topology on K.
A subdcpo P of a dcpo X is a subset P (implicitly ordered by the restriction of the ordering of X) that is closed under directed suprema, as computed in X; namely, a subset P ⊆ X such that for every directed family D of elements of P, the supremum x of D in X actually lies in P. Then x is in fact the supremum of D in P, so P is a dcpo. But one should beware that subsets P of a dcpo X that happen to be dcpos may not be subdcpos; the notion of subdcpo is stronger. For example, the collection HZ of closed subsets of a topological space Z is always a dcpo (even a complete lattice), and occurs as a subset of the dcpo (even a complete lattice, too) PZ of all subsets of Z. But the supremum of a family D ⊆ HZ in PZ, namely its union, is not closed in general, so HZ is not a subdcpo of PZ; rather, the supremum of D is the closure of the union.
Equally tricky is the fact that, given a subdcpo K of a dcpo X, the Scott topology on K, namely the topology of Kσ, may differ from the subspace topology induced by the inclusion of K in Xσ. This is why we require F to be a family of topological spaces (K, τ) where each K is a subset of X, but we will not require τ to be the subspace topology.
To be more precise, given a subdcpo K of a dcpo X, the (Scott) topology on Kσ must be finer than the subspace topology induced from Xσ. Indeed, given any open subset in the subspace topology, namely given any set of the form U ∩ K with U Scott-open in X, we see that U ∩ K is upwards-closed in K: if x≤y in K and x is in U ∩ K, then y is in U, hence in U ∩ K. Given any directed family D in K, with a supremum x in X—necessarily also its supremum in K, since K is a subdcpo of X—if x is in U ∩ K, then it is in U, hence some element of D is in U since U is Scott-open in X. Therefore U ∩ K is Scott-open in K.
The converse may fail, however; in other words, there are cases where K is a subdcpo of X, but some Scott-open subsets of K are not open in the subspace topology, namely cannot be written as U ∩ K with U Scott-open in X. Perhaps the simplest example of such a situation is the following, which bears some resemblance to Johnstone’s space (Exercise 5.2.15 in the book), but is different.
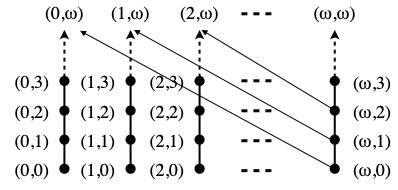
Example A. Let X be the product of N ∪ {ω} with itself, ordered as follows: (i, j) ≤ (k, l) if and only f i=k and j≤l, or i=l=ω and j≤k<ω. Hence, in order to go up in X, starting from (i, j), either you are in a finite column (i≠ω), and you have to increase j, or you are in the infinite column (i=ω), and you also have the choice of increasing j, but you may also go to any point (k, ω) with k≥j, k<ω if j≠ω, from which you will not be able to go higher up.
X is a dcpo, and its only non-trivial directed subsets (namely the only ones that do not already contain their supremum) are the sets D entirely contained in a single column (numbered i, in N ∪ {ω}), with elements (i, j) with arbitrarily high values of j; their supremum is (i, ω).
Let K be the subset of X consisting of the points in the top row, namely of the form (i, ω), i ∈ N ∪ {ω}. The ordering on K, inherited from X, is equality, hence K is trivially a dcpo. It is even a subdcpo of X: the only directed families in K are the one element sets {(i, ω)}, and their supremum in X, which is (i, ω), is clearly in K.
The Scott topology on K is the discrete topology: every subset of K is open (and closed) in Kσ. Hence {(ω, ω)} is open in Kσ. But it is not open in the subspace topology from Xσ: if {(ω, ω)} can be written as U ∩ K with U Scott-open in X, then U must contain points (ω, j) with arbitrary large values of j ∈ N, since the supremum of {(ω, j) | j ∈ N} is (ω, ω). Now (ω, j)≤(j ,ω), so (j ,ω) must be in U. It is in K, by definition of K, but is also distinct from (ω, ω). ☐
Topologies determined by, and colimits
Let us return to our main topic. We are interested in spaces X with a family F of topological spaces (K, τ), where each K is a subset of X, and where the topology of X is determined by F, in the sense that for every subset U of X, U is open in X if and only if U ∩ K is open in (K, τ) for every (K, τ) ∈ F. Lawson and Xu consider more specific families, which are countable and organized as a monotone sequence of subsets K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … , satisfying the property that ∪n ∈ N Kn = X. Each Kn is given a topology τn, and the inclusion maps in: Kn → Kn+1 is required to be continuous.
This is a special case of the well-known categorical notion of a colimit (see Section 4.12.3 in the book). This is defined as follows. A diagram in a category C is a functor F from a small category I (i.e., a category with only a set, not a proper class, of objects) to C. The situation considered by Lawson and Xu is the special case where I is the poset N, seen as a category (the objects are the natural numbers, and there is a unique morphism m → n from m to n if m≤n, and none otherwise), F(n) ≝ Kn, and F(m → n) is the inclusion map of Km into Kn. For that, we only need K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … , together with the fact that the inclusion maps in: Kn → Kn+1 must be continuous; the property ∪n ∈ NKn = X is meaningless at this stage.
A cocone over that diagram is an object X of C, together with morphisms in : F(n) → X for every object n of I (the cocone maps), such that in o F(m → n) = im for every morphism m → n in I. For example, in Lawson and Xu’s situation, namely if K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … and each Kn (with a topology τn) is a subset of a space X (with a topology τ), with a continuous inclusion map in of (Kn, τn) into (X, τ), then the pair (X, τ), (in)n ∈ N is a cocone of F in Top.
A colimit is a universal cocone, namely a cocone X, (in)n object of I of F such that for every cocone Y, (jn)n object of I of F, there is a unique morphism f : X → Y in C such that jn = f o in for every object n of I. In the situation considered by Lawson and Xu, (X, τ), (in)n ∈ N is a colimit of F in Top if and only ∪n ∈ N Kn= X, and the topology τ is determined by the family of spaces (Kn, τn). That it is really a colimit was proved as Lemma C of last month’s post, in the more general case where N is replaced by a general small category, and I called such colimits canonical rigid colimits. Since the indexing category is N, I called the resulting colimits ω-rigid colimits.
The main theorem of last month’s post, a slight improvement of a theorem of Lawson and Xu’s, is the following.
Theorem I. Let F, G : N → Top be two ω-rigid diagrams, where each space F(n) and each space G(n) is core-compact. Then colim (F × G) = colim F × colim G.
In the same post, we have seen various counterexamples showing that such commutations of colimits with products failed for other kinds of diagrams, or when the spaces F(n) or G(n) are not core-compact.
Rigid colimits, and directed rigid colimits in Posσ
Instead of computing colimits and products in the category Top of topological spaces and continuous maps, let us investigate what they are in the category Dcpo of dcpos and Scott-continuous maps, or more generally in the category Posσ of posets and Scott-continuous maps (not the category Pos of posets and monotonic maps).
We have seen in the post of November 20th, 2019, how one can build colimits in Dcpo, and that is not completely straightforward. Instead, we will look at simpler cases, which we will call rigid colimits, by imitation of the situation we have described in Top.
We recall that a subdcpo P of a dcpo X is a subset P that is closed under directed suprema, as computed in X; namely, a subset P such that for every directed family D of elements of P, the supremum x of D in X actually lies in P. A subdcpo is the same thing as a subset P of X that is a dcpo and such that the inclusion map i : P → X is Scott-continuous. Generalizing this situation, Lawson and Xu define a sub-d-poset P of a poset X as a subset such that the inclusion map i : P → X is Scott-continuous; equivalently, P is a sub-d-poset of X if and only if for every directed family D in P that has a supremum x in P, then x is also the supremum of D in X.
We define rigid colimits in Posσ very much as in Top. A rigid diagram in Posσ is a diagram F : I → Posσ where:
- every poset F(i) is a sub-d-poset of a common poset X, with X ≝ ∪i object of I F(i);
- for every morphism φ : i → j in I, F(φ) is the inclusion map of F(i) into F(j), and is required to be Scott-continuous;
- the Scott topology on X is determined by the spaces F(i)σ, where i ranges over the objects of I.
In condition 2, we may as well consider I to be a poset, since any two parallel arrows φ must be mapped by F to the same inclusion map, and then condition 2 expresses that for all pair of indices i and j such that i≤j in I, F(i) is a sub-d-poset of F(j).
Condition 3 is very strong. In order to explain it, we consider Posσ to be a full subcategory of Top, by equating every poset P with the topological space Pσ. (That Posσ is a full subcategory of Top means that a function f : X → Y between posets is Scott-continuous if and only if f is continuous from Xσ to Yσ: this is what Proposition 4.3.5 in the book says.) Then condition 3 expresses that the topological space Xσ is a (rigid) colimit of F in Top.
Lemma B. For every rigid diagram F : I → Posσ, the poset X ≝ ∪i object of I F(i) is a colimit of F in Posσ, with the inclusion maps of F(i) into X as cocone maps.
Proof. Let mi be the inclusion map of F(i) into X. By condition 1, each mi is Scott-continuous, and then it is easy to see that X, (mi)i object of I is a cocone over F in Posσ. Let Y, (pi)i object of I be a cocone over F in Posσ. Then Yσ, (pi)i object of I is a cocone over F in Top. By condition 3, Xσ, (mi)i object of I is a colimit of F in Top. Therefore there is a unique continuous map f : Xσ → Yσ such that f o mi = pi for every object i of I. In other words, there is a unique (Scott-)continuous map f : X → Y such that f o mi = pi for every object i of I. ☐
We will say that a diagram F : I → Posσ is directed if and only if I is a directed poset. This seems to be needed in Lemma C below.
There is a danger in equating Posσ with a full subcategory of Top, as we have done above: products are not computed the same way in the two categories. In order to avoid any confusion, we will keep using × for topological product, and we will use ×p to denote product in Posσ. For any two posets P and Q, P ×p Q is the collection of pairs (p, q) with p ∈ P and q ∈ Q, with the product ordering. We extend this notation to products of diagrams F : I → Posσ and G : J → Posσ, by letting F ×p G map every pair of objects i of I and j of J to F(i) ×p G(j).
The following says that poset products distribute over colimits of directed rigid diagrams in Posσ.
Lemma C. Given any two directed rigid diagrams F : I → Posσ and G : J → Posσ, with respective colimits X ≝ ∪i object of I F(i) and Y ≝ ∪j object of J G(j) in Posσ, the product diagram F ×p G is a directed rigid diagram with colimit X ×p Y.
Proof. The fact that F ×p G is directed, namely that the poset product I ×p J is directed, is clear. We verify conditions 1—3.
- Every (poset or topological) product F(i) ×p G(j) is a sub-d-poset of X ×p Y: this is clear, since directed suprema in products are computed componentwise.
- For all morphisms φ : i → i’ in I (i.e., if i≤i’ in I) and ψ : j → j’ in J (i.e., if j≤j’ in J), F(φ) × G(ψ) is a product of two inclusion maps, hence is itself an inclusion map, and it is Scott-continuous as a product of two Scott-continuous maps;
- The Scott topology on X ×p Y is determined by the spaces (F(i) × G(j))σ, (equivalently, F(i)σ × G(j)σ) where i ranges over the objects of I and j ranges over the objects of J. That is the difficult part. In one direction, given any Scott-open subset W of X ×p Y, W ∩ (F(i) ×p G(j)) is Scott-open in F(i) ×p G(j) because F(i) ×p G(j) is a sub-d-poset of X ×p Y, as we have seen in item 1. In the other direction, let W be a subset of X ×p Y such that W ∩ (F(i) ×p G(j)) is Scott-open in F(i) ×p G(j) for every object i of I and every object j of J.
- We verify that W is upwards-closed. Let (x, y) ∈ W, and let (z, t) be such that x≤z in X and y≤t in Y. Each of the two pairs (x, y) and (z, t) is in some product F(i) ×p G(j), and we can choose the same i and the same j for both, because I ×p J is directed. Then (x, y) ∈ W ∩ (F(i) ×p G(j)), W ∩ (F(i) ×p G(j)) is Scott-open hence upwards-closed in F(i) ×p G(j), so (z, t) ∈ W ∩ (F(i) ×p G(j)), and therefore (z, t) ∈ W.
- Let (x, y) ∈ W, and let us imagine that (x, y) is the supremum of a directed family (xk, yk)k ∈ K in X ×p Y. We form the set W|y ≝ {z ∈ X | (z, y) ∈ W}. There is an index j in J such that y ∈ G(j). For every object i of I, W|y ∩ F(i) = (W ∩ (F(i) ×p G(j)))|y. Since W ∩ (F(i) ×p G(j)) is Scott-open in F(i) ×p G(j), it is easy to see that (W ∩ (F(i) ×p G(j)))|y is Scott-open in F(i): the main part of the argument is that for every directed family (x’p)p ∈ P in F(i) whose supremum x’ is in (W ∩ (F(i) ×p G(j)))|y, (x’, y) is the supremum of the directed family (x’p, y)p ∈ P in F(i) ×p G(j) and lies in W ∩ (F(i) ×p G(j)), so some (x’p, y) is in W ∩ (F(i) ×p G(j)), meaning that some x’p is in (W ∩ (F(i) ×p G(j)))|y. Now that we know that (W ∩ (F(i) ×p G(j)))|y is Scott-open in F(i), namely that W|y ∩ F(i) is Scott-open, for every object i of I, we obtain that W|y is Scott-open in X; this is because the Scott topology on X is determined by the spaces F(i)σ, where i ranges over the objects of I.
Since (x, y) is the supremum of the directed family (xk, yk)k ∈ K in X ×p Y, hence in particular x is the supremum of (xk)k ∈ K in X, and since (x, y) ∈ W, we have x ∈ W|y, so some xk is in W|y. In other words, (xk, y) is in W for some k ∈ K.
As with the W|y construction, the set W|xk ≝ {t ∈ Y | (xk, t) ∈ W} is Scott-open in Y, using the fact that the Scott topology on Y is determined by the spaces G(j)σ, where j ranges over the objects of J.
Since (x, y) is the supremum of the directed family (xk’, yk’)k’ ∈ K in X ×p Y, hence in particular y is the supremum of (yk’)k’ ∈ K in Y, and since (xk, y) ∈ W, we have y ∈ W|xk, so some yk’ is in W|xk. In other words, (xk, yk’) is in W for some k’ ∈ K.
Now there is an index l in K such that (xk, yk) and (xk’, yk’) are both below (xl, yl). In particular, xk≤xl and yk’≤yl. Since W is upwards-closed, (xl, yl) is in W. This shows that W is Scott-open in X ×p Y. ☐
The core of Lawson and Xu’s argument
We finally arrive at the core of Lawson and Xu’s approach.
Let us call gentle (my way of calling it) any class C of posets such that (P × Q)σ = Pσ × Qσ for all P, Q in C; or rather, to be precise, (P ×p Q)σ = Pσ × Qσ.
Consider any two directed rigid diagrams F : I → Posσ and G : J → Posσ. We form their colimits X ≝ ∪i object of I F(i) and Y ≝ ∪j object of J G(j) in Posσ, and we notice that Xσ and Yσ are the colimits of the same diagrams in Top, by condition 3. In short (and ignoring cocone maps, which are uniquely determined as inclusions anyway), Xσ = colim F and Yσ = colim G, where colim denotes colimits in Top. If each F(i) and each G(j) is in a given gentle class C, and if colim (F × G) = colim F × colim G (where colim denotes colimit in Top, once again, and where × is product in Top), then Xσ × Yσ = colim F × colim G = colim (F × G) = colim (F ×p G). By Lemma C, F ×p G is a directed rigid diagram with colimit X ×p Y, and therefore its colimit in Top, colim (F ×p G), is (X ×p Y)σ. We sum this up as follows.
Theorem D. For every gentle class of posets C, for every class D of directed rigid diagrams F : I → Posσ such that F(i) ∈ D for every i in I and such that colim (F × G) = colim F × colim G for all F : I → Posσ and G : J → Posσ in D (i.e., such that topological products distribute over colimits), the class of posets obtained as colimits in Posσ of diagrams in D is gentle.
Topological products rarely distribute over colimits, as we have seen last month. One of the largest possible situations is given in Theorem I, which we have recalled earlier in this post. Just like in Top, we say that an ω-rigid diagram in Posσ is a directed rigid diagram F : I → Posσ with I=N. Explicitly, an ω-rigid diagram in Posσ is a countable monotone sequence K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … of sub-d-posets Kn (n ∈ N—namely, Kn=F(n)) of a common poset X such that:
- ∪n ∈ N Kn = X;
- the Scott topology of X is determined by the collection of spaces Kn, each with its Scott topology.
Notice that the inclusion map in : Kn → Kn+1 is automatically Scott-continuous for every n ∈ N: for every directed family D with a supremum x in Kn, x is also the supremum of D in X, hence also its supremum in its subset Kn+1. Hence such diagrams are (directed) rigid diagrams in Posσ. Equating posets with the topological spaces one obtains by giving them the Scott topology, every ω-rigid diagram in Posσ is an ω-rigid diagram in Top (the topologies τn on each Kn being Scott topologies).
The colimits (in Posσ, or in Top) of ω-rigid diagrams of locally compact posets in Posσ are what Lawson and Xu call lcω-posets. Let me call ccω-poset any colimit of ω-rigid diagrams of core-compact posets in Posσ.
The following corollary follows from Theorem D, together with the fact that core-compact posets form a gentle class: for all posets P and Q, if Pσ and Qσ are core-compact (in fact if just one of them is), then (P × Q)σ = Pσ × Qσ. I have recalled this fact at the beginning of this post; see the Proposition after item 1(a) in the post of March 20th, 2022. This (slightly) generalizes Theorem 4.10 of [2].
Corollary E. The ccω-posets, namely the colimits of ω-rigid diagrams F : N → Posσ such that F(n) is core-compact for every n ∈ N, form a gentle class: for all ccω-posets P and Q, (P × Q)σ = Pσ × Qσ.
- Hualin Miao, Xiaoyong Xi, Qingguo Li, and Dongsheng Zhao. Not every countable complete distributive lattice is sober, Mathematical Structures in Computer Science33(9):809–831, October 2023. arXiv version arXiv:2205.00250v1 [math.GN], 30 Apr 2022.
- Jimmie Lawson and Xiaoquan Xu. Spaces determined by countably many locally compact subspaces. Topology and its Applications, 354, 108973, 2024.

— Jean Goubault-Larrecq (September 21st, 2024)
