My initial plan this month was to explain the main construction of a recent paper by Jimmie Lawson and Xiaoquan Xu [1]. Well, not just explaining, but also extending slightly, and providing counterexamples showing that you cannot extend that much, and in the end, the post became too big. Hence I will split the post in two. The result is still pretty long. I did not post anything last month… what did you expect? 🙂
It turns out that the Lawson-Xu construction deeply relies on a result that says that products distribute over certain kinds of colimits in the category Top of topological spaces; at least that is one way of presenting it. That is the only thing I will deal with this month, and I will explain the connection to the Lawson-Xu result next month.
Colimits
I have explained what colimits are in Section 4.12.3 of the book. This is defined as follows. A diagram in a category C is a functor F from a small category I (i.e., a category with only a set, not a proper class, of objects) to C.
A cocone over that diagram is an object X of C, together with morphisms in : F(n) → X for every object n of I (the cocone maps), such that in o F(m → n) = im for every morphism m → n in I.
A colimit is a universal cocone, namely a cocone X, (in)n object of I of F such that for every cocone Y, (jn)n object of I of F, there is a unique morphism f : X → Y in C such that jn = f o in for every object n of I.
Colimits in Top are computed as quotients of coproducts (Example 4.12.12 in the book). Explicitly, this means the following. Let F : I → Top be a diagram in Top. Up to isomorphism, its colimit is the quotient ∑i object of I F(i)/≡, where the coproduct ∑i object of I F(i) is the collection of pairs (i, x) where i is an object of I and x is a point of F(i), with the topology defined by basic open sets {i} × U (U open in X), and ≡ is the smallest equivalence relation on ∑i object of I F(i) such that (i, x)≡(k, F(φ)(x)) for every morphism φ : i → k in I and for every x ∈ F(i). The topology on ∑i object of I F(i)/≡ is the quotient topology. Writing q for the quotient map, and mi for the inclusion x ↦ (i, x) of F(i) into the coproduct ∑i object of I F(i), the cone maps from F(i) to ∑i object of I F(i)/≡ are q o mi.
We will need to understand how ≡ is built. Let us write ⇒ for the binary relation such that (i, x) ⇒ (k, F(φ)(x)) for every morphism φ : i → k in I and for every x ∈ F(i). Then (i, x)≡(k, z) if and only if there is a (finite) zigzag (i, x) ⇒ ⇐ ⇒ … ⇐ ⇒ (k, z) (possibly of length 0). Indeed, ⇒ is reflexive, and this is a classical way of defining the smallest equivalence relation containing the reflexive relation ⇒.
The construction of colimits in the category Set of sets is exactly the same, except that we don’t need to care about topologies.
Distributing products over colimits
The question I want to address today is the following. Let F : I → Top and G : J → Top be diagrams in Top. Then F × G : I × J → Top, which maps every object (i, j) to F(i) × G(j) and every morphism φ×ψ : (i, j)→ (k, l) of I × J (namely, φ is a morphism from i to k in I and ψ is a morphism from j to l in J) to F(φ) × G(ψ), is a diagram; we wish to know when the product X × Y of the colimits of F and G is the colimit Z of F × G (up to isomorphisms of cocones, namely up to homeomorphism of X × Y onto Z that commutes with the cocone maps).
That seems very natural, and you should be able to convince yourself that there is a bijection between the product of the colimits colim F and colim G and the colimit colim (F × G), which maps every pair ([(i, x)], [(j, y)]) (where x ∈ F(i), y ∈ G(j), and the square bracket notation […] denotes equivalence classes with respect to the equivalence relations used to define the relevant colimits) to the equivalence class [((i, j), (x, y))]. That bijection commutes with all the cocone maps, too, but is it a homeomorphism?
If so, then that bijection will provide us with an isomorphism of cocones between colim F × colim G and colim (F × G) in Top, namely that that product distributes over those colimits.
As I will demonstrate, this happens very rarely; and Lawson and Xu have found one of the most general cases that products distribute over colimits in Top.
First failures: products do not distribute over coequalizers (quotients)
The first cases we will explore are when colimits are obtained as quotients.
Example A. We can realize any topological quotient X/≡ as a coequalizer, namely as a specific colimit (see comment after Example 4.12.11 in the book). Explicitly, let q : X → X/≡ be the quotient map. We form ker(q,q) ≝ {(x, y) ∈ X × X | q(x)=q(y)}, with the subspace topology. There are two projection maps p1 and p2 from ker(q, q) to X, mapping (x, y) to x and to y respectively. Then X/≡, with cone maps q : X → X/≡ and q o p1 = q o p2 : ker(q,q) → X/≡, forms a coequalizer of p1 and p2.
Formally, this is a colimit of a diagram F on a category I with two objects and two parallel non-identity morphisms, mapped to p1 and p2 respectively. Hence that is a pretty simple form of colimit.
For G, we resort to an even simpler kind of colimit. We let J be the category with one object and one morphism (the identity), and we let G map the unique object to some arbitrary space Y (and the identity morphism to the identity map on Y). Then the colimit of G is simply Y, with identity as a cocone map.
If product distributes over the colimits of F and G, then (X/≡) × Y is a colimit of F × G, with cone maps q × id : X × Y → (X/≡) × Y and (q o p1) × id= (q o p2) × id: ker(q,q) × Y → (X/≡) × Y. In particular, q × id is a quotient map. But, with Y fixed, that is the case for every space X and every equivalence relation ≡ on X, if and only if Y is core-compact (Exercise 5.4.29 in the book).
Hence, by taking any non-core-compact space for Y, for example Q, there must be a space X and an equivalence relation ≡ on X such that the product of the colimits of F and G, as built above, is not a colimit of F × G. (End of Example A.) ☐
Second failures: colimits of core-compact spaces
But maybe products would distribute over colimits of core-compact spaces, or of locally compact spaces? That is wrong, too, as the following example shows. The example shows that products still fail to distribute over very specific colimits (namely, quotients) of stably compact spaces, even of spectral spaces, even of algebraic bc-domains in their Scott topology.
Example B. We consider the complete lattice Lfan, which we studied in the post of May 20th, 2024. The elements of Lfan are ⊥, ⊤ and all pairs (m, n) of natural numbers, ordered by x≤y if and only if x=⊥, or y=⊤, or x is a pair (m, n) and y is a pair (m’, n’) with m=m’ and n≤n’. See the picture below.
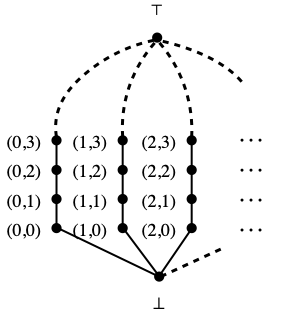
Proposition I of the aforementioned post states that Lfan is not core-compact in its Scott topology. But Lfan arises as a topological quotient, as we now see. Let Nω be the dcpo of natural numbers with an extra element ω above all natural numbers, with the Scott topology. Let Z be the (topological) coproduct of countably many copies of Nω. The elements of Z are the pairs (m, n) with m ∈ N and n ∈ Nω, and its open subsets are the sets Vf ≝ {(m, n) ∈ Z | m ∈ dom f and n≥f(m)}, where f ranges over the partial functions from N to N. Then we form the lifting Z⊥, obtained by adding a fresh element ⊥ to Z, and whose open subsets are the open subsets of Z plus Z⊥ itself.
We claim that the map q : Z⊥ → Lfan that sends ⊥ to ⊥, every pair (m, n) with n≠ω to itself, and every pair (m, ω) to ⊤, is a quotient map. By Lemma E of the same post as above, the (Scott-)open subsets of Lfan are exactly the sets Uf, where f ranges over the (total) functions from N to N, plus the empty set, plus the whole space Lfan. See the following picture.
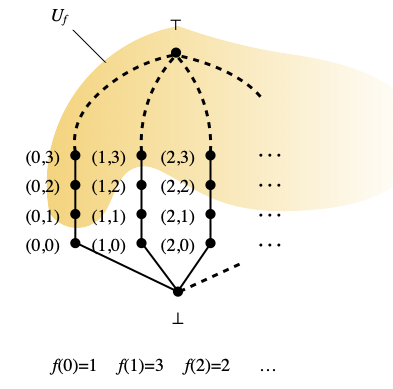
We have q–1(Uf) = Vf, so q is continuous. It is clear that q is surjective. Finally, let us imagine that q–1(U) is open in Z⊥; we will show that U is open in Lfan. If q–1(U) is the whole of Z⊥, then U is the whole space Lfan, which is open. Otherwise, q–1(U) = Vf for some partial map from N to N. If dom f is empty, then Vf is empty, so U is empty, hence open. Otherwise, Vf contains some point (m, ω), hence all points (m, ω), which have the same image under q. This entails that f is in fact a total function, and then r–1(Uf) = Vf, which implies that U=Uf, using the surjectivity of q.
Now let us consider any function h : N × N → N such that h(m,_) is unbounded for every natural number m, and such that h(_,m’) is unbounded for every natural number m’. For example, h(m,m’) ≝ m+m’ fits. Let W be the subset of Lfan × Lfan consisting of all pairs ((m,n), (m’,n’)) such that n, n’ ≥ h(m,m’), and all the points above them (namely, the points ((m,n), ⊤) such that n≥h(m,m’) for some m’ ∈ N, the points (⊤, (m’,n’)) such that n’≥h(m,m’) for some m’ ∈ N, and the point (⊤, ⊤)).
We claim that the inverse image (q × q)–1 (W) is open in Z⊥ × Z⊥. It will be useful to realize that (q × q)–1 (W) is upwards-closed: indeed, q is continuous hence monotonic, so q × q is monotonic, too, and W is upwards-closed. Any element of (q × q)–1 (W) must be in Z × Z, namely of the form ((m,n), (m’,n’)) with m, m’ ∈ N and n, n’ ∈ Nω. We will find an open rectangle containing ((m,n), (m’,n’)) and included in (q × q)–1 (W).
- If n, n’ ≠ ω, then ((m,n), (m’,n’)) is in Vf ×Vg, where f is only defined at m and f(m)≝n, and g is only defined at m’ and g(m’)≝n’. Vf ×Vg is simply the upward closure of ((m,n), (m’,n’)) in Z⊥ × Z⊥, and since (q × q)–1 (W) is upwards-closed, Vf ×Vg is included in (q × q)–1 (W).
- If n≠ω and n’=ω, then we observe that there must be a natural number n” such that ((m,n), (m’,n”)) ∈ (q × q)–1 (W): any number larger than or equal to h(m,m’) will fit. Then we have seen that there is an open rectangle containing ((m,n), (m’,n”)) and included in (q × q)–1 (W), and that open rectangle must also contain ((m,n), (m’,ω))=((m,n), (m’,n’)). We reason similarly with n=ω, or when n=n’=ω.
But W is not open in Lfan × Lfan: given any point (x, y) of W, we show that no open rectangle containing (x, y) can be included in W. Any open rectangle containing (x, y) must be of the form Uf ×Ug, or Uf × Lfan, or Lfan ×Ug, where f, g : N→ N are (total) functions. The sets Uf × Lfan, or Lfan ×Ug are not included in W, because W contains no point with a ⊥ at any position. The set Uf ×Ug cannot be included in W either, because Uf ×Ug contains all the points ((m, f(m)), (m’, g(m’)) with m, m’ ∈ N, and they are in W if and only if f(m)≥h(m, m’) and g(m’)≥h(m, m’) for all m, m’ ∈ N; but, since h is unbounded in each of its coordinates, there is no m ∈ N such that f(m)≥h(m, m’) for every m’ ∈ N (and there is no m’ ∈ N such that g(m’)≥h(m, m’) for every m ∈ N).
Therefore q × q is not a quotient map, although Z⊥ × Z⊥ is a product of core-compact spaces.
In fact Z⊥ is not just a core-compact space, but even an algebraic bc-domain in its Scott-topology (whose finite points are all the points (m, n) with n≠ω, plus ⊥), which implies that it is stably compact, and even spectral. (End of Example B.) ☐
Intermission: the categorical view
The reason why I focussed on core-compact spaces in the previous section is that the core-compact spaces are exactly the exponentiable objects in Top (see Section 5.4 in the book). There is a short categorical proof that products distribute over colimits in every Cartesian-closed category, namely in categories in which every object is exponentiable. (For example, in Set, and this is why there is a natural bijection between colim F × colim G and colim (F × G), and the only issue is whether this bijection is a homeomorphism.) A Cartesian-closed category is one where every object is exponentiable, but maybe we could adapt the proof and only assume that certain, not all, objects, are exponentiable?
Well, the spaces Z⊥ which we took the quotients (colimits) of in Example B are core-compact, so we know that this hope is doomed. Let us still try to understand what fails.
Here is the short categorical proof that products distribute over colimits in Cartesian-closed categories. As with most “short” proofs, it is short by virtue of hiding a lot of details. My point is to understand what fails if we only assume F and G to map objects to exponentiable objects instead of assuming that the whole category is Cartesian-closed.
We will write [X → Y] for the exponential object (the set of continuous maps from X to Y, with the core-open topology, see Theorem 5.4.4 in the book) when X is exponentiable (core-compact).
For every object Z of a category C, the contravariant homset functor HomC(_, Z) (namely, the functor from C to Set that maps every object X to HomC(X, Z), and every morphism f: X → Y to the function g ∈ HomC(Y, Z) to g o f ∈ HomC(X, Z) maps colimits to limits. This is not a difficult result, see Proposition 2.9.5 of [2], for example. Writing colimi F(i) instead of colim F, colimj G(j) instead of colim G, etc., for more readability, there is also a statement on double limits in Set that limi,j H(i, j) ≅ limj limi H(i, j) (for any diagram H with double indices). Then, for every object Z of C (Top, in our case):
| HomC(colimi,j (F(i) × G(j)), Z) | ≅ limi,j HomC(F(i) × G(j), Z) | |
| ≅ limi,j HomC(F(i), [G(j) → Z]) | G(j) is exponentiable | |
| ≅ limj limi HomC(F(i), [G(j) → Z]) | double limits | |
| ≅ limj HomC(colimi F(i), [G(j) → Z]) | ||
| ≅ limj HomC(colimi F(i) × G(j), Z) | G(j) is exponentiable | |
| ≅ limj HomC(G(j), [colimi F(i) → Z]) | (*) | |
| ≅ HomC(colimj G(j), [colimi F(i) → Z]) | ||
| ≅ HomC(colimj F(i) × colimi G(j), Z) | (*) |
The two rows marked (*) are only justified if colimi F(i) is exponentiable. If that is true, then the isomorphism HomC(colimi,j (F(i) × G(j)), Z) ≅ HomC(colimj F(i) × colimi G(j), Z) we obtain this way, for every object Z, is enough to show that colimi,j (F(i) × G(j)) ≅ colimj F(i) × colimi G(j) (up to lots of omitted details). In Example B, colimi G(j) is Lfan, but precisely, Lfan is not exponentiable.
There is another categorical line of attack to the problem of products and colimits. Given any productive class C of topological spaces, the category TopC of C-generated spaces is Cartesian-closed (see Theorem 5.6.12 and Exercise 5.6.19 in the book). By Proposition 5.6.16 in the book, and if C is non-empty, then the C-generated spaces are the quotients of coproducts of objects of C. Also, colimits in TopC are computed exactly as in Top (Fact 5.6.14 in the book). The issue there is that products are computed differently; see Theorem 5.6.12 in the book.
Third failures: rigid colimits
Before the intermission, we have seen that quotients behave badly with products in Top; so let us try and get rid of quotients entirely. It is not difficult to see that products distribute over coproducts (indexed by any set I), namely over disjoint unions. But we would like to consider non-disjoint unions, too.
Hence we will look at rigid colimits. The term “rigid” is non-standard, and I will use it to denote colimits of rigid diagrams, namely diagrams F : I → Top where every space F(i) is a topological space (Ki, τi), each Ki is a subset of a common set X, independent of i, and F(φ) is the inclusion map (Ki, τi) → (Kj, τj) for every morphism φ : i → j in I. (In particular, F maps any two parallel arrows to the same morphism, so there is really no point in considering a general small category for I: a preordered set, considered as a category, suffices.) The colimits considered by Lawson and Xu are rigid. They also require I to be countable, and really to be the poset N of natural numbers, and they require each space F(i) to be locally compact; we will not make such restrictions, at least for now, but we will see that most of them are in fact needed.
In the definition of rigid colimits, and without loss of generality, we may assume that X is the union of the sets Ki. Then (X, τ) is a colimit of F in Top, where τ is the topology determined by the spaces (Ki, τi), in the sense that a subset U of X is open in τ if and only if U ∩ Ki is open in τi for every object i of I. We will call it the canonical (rigid) colimit of F, and we will write it as colim F. This is really the colimit, as we now check.
Lemma C. Let F : I → Top be a rigid diagram, X ≝ ∪i object of I F(i), and τ be the topology on X determined by the spaces F(i). Then (X, τ), with the inclusion maps mi from F(i) into X, is a colimit of F.
Proof. We know how to build a colimit of F, and we will simply show that it is isomorphic to the canonical colimit. The usual way of building the colimit of F is as ∑i object of I F(i)/≡, where ∑i object of I F(i) has the coproduct topology and ≡ is the smallest equivalence relation on ∑i object of I F(i) such that (i, x)≡(k, F(φ)(x)) for every morphism φ : i → k in I and for every x ∈ F(i); in other words, such that (i, x)≡(k, x) for every morphism φ : i → k in I. Let us write q for the quotient map ∑i object of I F(i) → ∑i object of I F(i)/≡. The cocone maps ji : F(i) → ∑i object of I F(i)/≡ send every point x of F(i) to the equivalence class q (i, x) of (i, x).
By definition of ≡, if (i, x)≡(k, y) then x=y. Indeed, remember that (i, x)≡(k, y) if and only if there is a zigzag (i, x) ⇒ ⇐ ⇒ … ⇐ ⇒ (k, z), where ⇒ is the binary relation defined by (i, x) ⇒ (k, F(φ)(x)) (i.e., (i, x) ⇒ (k, x)) for every morphism φ : i → k in I and for every x ∈ F(i). The claim follows by an induction on the number of arrows in the zigzag.
It follows that there is a well-defined map f : ∑i object of I F(i)/≡ → X that sends the equivalence class of (i, x) to x. Then f is a bijection, whose inverse maps every point x of X to the equivalence class of (i, x), where i is any object of I such that x ∈ F(i); that exists because X = ∪i object of I F(i).
For every open subset U in the topology τ, we verify that f–1(U) is open in ∑i object of I F(i)/≡. It suffices to show that q–1(f–1(U)) is open in ∑i object of I F(i). But q–1(f–1(U)) is the collection of pairs (i, x) such that x ∈ F(i) and f(q(i, x))=x is in U, namely the union of the sets F(i) ∩ U (more precisely, {i} × (F(i) ∩ U)—we silently equate F(i) with a subset of ∑i object of I F(i)) over all objects i of I. By definition of τ as the topology determined by the spaces F(i), each of those sets F(i) ∩ U is open in F(i), so their union is open in ∑i object of I F(i). This shows that f is continuous.
In order to show that f is a homeomorphism, we need to show that the direct image of any open subset of ∑i object of I F(i)/≡ is open. An open subset V of ∑i object of I F(i)/≡ is a subset such that q–1(V) is open in ∑i object of I F(i), namely such that {x ∈ F(i) | (i, x) ∈ q–1(V)} is open in F(i) for every object i of I. Its direct image U is the collection of points obtained as the image under f of the equivalence classes of pairs (i, x) in {x ∈ F(i) | (i, x) ∈ q–1(V)}, namely {f (q (i, x)) | i object of I, x ∈ F(i), (i, x) ∈ q–1(V)} = ∪i object of I{x ∈ F(i) | (i, x) ∈ q–1(V)}. For every object i of I, F(i) ∩ U is then equal to {x ∈ F(i) | (i, x) ∈ q–1(V)}, which is open in F(i). Since τ is determined by the spaces F(i), U itself is open in (X, τ). Therefore f–1 is continuous, and f is a homeomorphism.
It remains to show that f is compatible with the cocone maps, namely that f o ji = mi for every object i of I. Explicitly, f o ji maps every point x of F(i) to f (q (i, x)) = x, and that is equal to mi (x). ☐
Do products distribute over rigid colimits in Top? Well, no, not in general. We will produce a counterexample based on a very specific form of rigid diagrams. Beware that this is a pretty complicated counterexample.
Let an identity diagram be any rigid diagram F : I → Top where each F(i) is actually the same set X, with a topology τi that depends on i, and where the maps F(φ) : (X, τi) → (X, τj), for each morphism φ : i → j in I, are identity maps. The requirement that F(φ) be continuous is equivalent to the fact that τi be finer than τj, for each φ : i → j in I. Using Lemma C, the canonical colimit of F is X, with the topology ∩i object of I τi. Indeed, a set that is open in the topology determined by every (X, τi) is a set (whose intersection with X, namely itself) is open in τi for every object i of I.
Example D. We let F : I → Top be the (identity) diagram where I contains of just one object * and one identity morphism, and F(*) ≝ Lfan. We consider it with its Scott topology, and we remember from Lemma E of the post of May 20th, 2024 (or from Example B) that its (Scott-)open subsets are itself, the empty set, and the sets Uf, where f ranges over the total functions from N to N. The colimit of F is Lfan (with the obvious cocone map).
The description of G : J → Top is more complicated. Since G is going to be a rigid colimit, let me say right away that the common set of which every G(j) will be a subset will be O(Lfan), the collection of Scott-open subsets of Lfan.
Let us write Nω for the set of natural numbers N, with an extra element ω above all natural numbers. (No, this will not be the indexing category J! I need quite some preparation, and J will be way more complicated… please bear with me.) We order Nω in the usual way: 0 ≤ 1 ≤ … ≤ n ≤ … ≤ ω.
For every function g from N to Nω, let dom g be the set of numbers m ∈ N such that g(m)≠ω. This is the domain of g, following a convention that we used in the the post of June 20th, 2024 on the study of Lfan. We let FF be the set of functions f from N to Nω whose domain is finite, ordered pointwise.
For any function g from N to Nω, whether its domain is finite or not, let Vg be the collection of Scott-open subsets of Lfan of the form Uf with f≤g, plus Lfan itself. By Proposition D of the post of June 20th, 2024, the empty set, {Lfan}, the whole space O(Lfan), and the sets Vg, where g ranges over FF, are the Scott-open subsets of O(Lfan). (Proposition D states that all but the first kind form a base of the Scott topology on O(Lfan). But the equality ∪i ∈ I Vgi = Vg, where g≝supi ∈ I gi, for every non-empty index set I, and a bit of a case analysis shows our claim.)
We will design G so that its colimit is exactly O(Lfan) with its Scott topology. By Exercise 5.2.7 of the book, and since Lfan is not core-compact (Proposition I of the post of May 20th, 2024), the set (∈) ≝ {(x, U) | x ∈ U, U ∈ O(Lfan)} is not open in the product topology on Lfan × O(Lfan) (namely in colim F × colim G), and we will design G so that (∈) is open in colim (F × G).
What is more complex about the diagram G : J → Top is (mostly) the structure of the indexing poset J: this will be the poset of all (total) functions from N to N, ordered pointwise. Note that this is not countable. For each j ∈ J, let τj be the coarsest topology on O(Lfan) that contains the Scott topology (namely, the empty set, the whole space, and all the sets Vg with g ∈ FF) and all the sets Vf with f≥j, f : N → N. (For simplicity, we will consider any function f : N → N as a function from N to Nω whose domain is the whole of N.) We define G(j) as O(Lfan), with the topology τj. If j≤k in J, then τj is finer than τk, so this defines an identity diagram.
- There is an explicit description of the elements of τj: those are the empty set, {Lfan}, the whole space O(Lfan), and all the sets Vg where g ranges over the set FFj of functions from N to Nω that are above j except at finitely many points, namely such that domj g ≝ {m ∈ N | g(m) < j(m)} is finite.
Indeed, in one direction, if domj g is finite, then let g’ map every m ∈ domj g to g(m) and all other points to ω, then g’ is in FF and g is the pointwise minimum of g’ and j, so Vg = Vg’ ∩ Vj, showing that Vg is in τj.
In the other direction, we note that the sets Vg with g ∈ FFj (plus the empty set, {Lfan}, and the whole space O(Lfan)) form a topology that contains the sets Vg with g ∈ FF, the sets Vf with f≥j and dom f=N, and {Lfan}. Using the equalities Vg ∩ Vg’ = Vmin(g,g’) (with domj (min (g, g’)) = domj g ∪ domj g’) and ∪i ∈ I Vgi = Vg where g≝supi ∈ I gi, (with domj g = ∩i ∈ I domj gi) for every non-empty index set I, plus the fact that the empty intersection is the whole space O(Lfan), and the empty union is the empty set, we see that the sets Vg with g ∈ FFj, plus the empty set, {Lfan}, and O(Lfan), indeed form a topology τ. (Yes, that involves some case analysis, which I will not do explicitly. Please note that Lfan is inside every set Vg; if you don’t see why, go back to the place where we defined Vg.) That topology τ contains every set Vg with g ∈ FF, since then dom g, which is finite, contains domj g, so the latter is finite. It also contains every set Vf with f≥j, dom f=N, because domj f is empty in that case. That τ contains {Lfan} is by definition of τ. - As a consequence, ∩j ∈ J τj coincides with the Scott topology on O(Lfan). Every set Vg with g ∈ FF is in every τj, as well as {Lfan}, as we have just seen, so every Scott-open subset of O(Lfan) is in ∩j ∈ J τj. Conversely, let us consider any element W of ∩j ∈ J τj. If W is empty or {Lfan} or the whole of O(Lfan), then W is certainly Scott-open in O(Lfan). Otherwise, since W is in τj (for any j in J), it is of the form Vg, and domj g is finite (for every j in J). We claim that dom g is finite. Otherwise, let j map every element m of dom g to g(m)+1 (a natural number) and all other elements to some arbitrary natural number. Then domj g contains at least all the points of dom g, and that is impossible if dom g is infinite. Therefore W = Vg where g is in FF, so W is Scott-open in O(Lfan).
- Finally, we claim that (∈) ≝ {(x, U) | x ∈ U, U ∈ O(Lfan)} is open in colim (F × G), namely that it is open in the product of the Scott topology on Lfan and of the topology τj on O(Lfan), for every j in J. We fix an arbitrary j in J (a function from N to N), and a point (x, U) of (∈). We will find an open rectangle containing (x, U) and included in (∈).
We get rid of a few trivial cases first: if U=Lfan, then the open rectangle Lfan × {Lfan} fits; this includes the case where x=⊥, since in that case U must be equal to Lfan. Hence we may assume that x≠⊥, and that U is neither empty nor Lfan. In particular, U is equal to Uf for some (total) function f from N to N. If x=⊤, we let g ≝ max(f, j), the pointwise maximum of f and j; otherwise, x is a pair (m, n), and we define g as mapping m to f(m) and all other natural numbers to their image under max(f, j). In both cases, x is in Ug, which is Scott-open in Lfan. Also, Vg is in τj, namely there are only finitely many natural numbers m’ such that g(m’)<j(m’): in fact, there is only one, which must be m, and only in the case where x is of the form (m, n), since for all others, g(m’) = max(f (m’), j (m’)) ≥ j(m’). We note that U=Uf is in Vg, since f≤g. (For every m’ except possibly when m’=m in the case that x=(m, n), f(m’) ≤ max (f (m’), j (m’)) = g(m’), otherwise f(m’)=f(m)=g(m).) Hence Ug × Vg is an open rectangle (in the product of the Scott topology on Lfan with τj) that contains (x, U).
It remains to show that Ug × Vg is included in (∈). The pairs ((m’, n’), Uf’) that lie in Ug × Vg are such that n’≥g(m’) and f’ ≤ g, so n’≥f’(m’), namely (m’, n’) ∈ Uf’; and the pairs (⊤, Uf’) are all in (∈), whatever f’ is.
We have found an open subset (∈) of colim (F × G) that is not open in colim F × colim G, so products do not distribute over colimits in this case. (End of Example D—at last!) ☐
What allows Example D to go through is: on the left side, we have a non-core compact space, and that is a (pretty trivial) colimit of non-core compact spaces, and on the right side, we have a rather simple, but uncountable, colimit of spaces (which are all core-compact; I will leave that as an exercise—hoping that I am not mistaken).
Lawson and Xu’s situation where products distribute over colimits in Top
Although they do not formulate it this way, Lawson and Xu consider what I will call ω-rigid diagrams, namely rigid diagrams F : N → Top over the poset N, seen as category (i.e., I≝N), equivalently a countable monotone sequence K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … of subsets Kn (n ∈ N) of a common set X, with:
- ∪n ∈ N Kn = X,
- each Kn coming with a topology τn (the pair (Kn, τn) is the value of F(n)),
- with the property that the inclusion map in : (Kn, τn) → (Kn+1, τn+1) is continuous for every n ∈ N—equivalently, that for every open subset U of (Kn+1, τn+1), U ∩ Kn is open in (Kn, τn).
This takes care of the issue with rigid diagrams over an uncountable index sets, such as the diagram G of Example D.
Lawson and Xu also require each (Kn, τn) to be locally compact. I will argue that you only need each (Kn, τn) to be core-compact, and that is slightly more general. But it will be easier to understand the locally compact case first.
Theorem E [1, Theorem 3.3]. Let F, G : N → Top be two ω-rigid diagrams, where each space F(n) and each space G(n) is locally compact. Then colim (F × G) = colim F × colim G.
In other words, let K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … be a monotone sequence of subsets Kn (n ∈ N) of a common set X, with ∪n ∈ N Kn = X, let τn be a topology on Kn that makes it locally compact, and let us assume that the inclusion map in : (Kn, τn) → (Kn+1, τn+1) is continuous for every n ∈ N, namely that for every open subset U of (Kn+1, τn+1), U ∩ Kn is open in (Kn, τn).
Let L0 ⊆ L1 ⊆ … ⊆ Ln ⊆ … be a monotone sequence of subsets Ln (n ∈ N) of a common set Y, with ∪n ∈ N Ln = Y, let τ’n be a topology on Ln that makes it locally compact, and let us assume that the inclusion map jn : (Ln, τ’n) → (Ln+1, τ’n+1) is continuous for every n ∈ N, namely that for every open subset V of (Ln+1, τ’n+1), V ∩ Ln is open in (Ln, τ’n).
Then the theorem claims that the topology determined by the spaces (Km, τm) × (Ln, τ’n), where m, n ∈ N, coincides with the product topology on (X, τ) × (Y, τ’), where τ is the topology determined by the spaces (Km, τm) and τ’ is the topology determined by the spaces (Ln, τ’n). Lawson and Xu call colimits of ω-rigid diagrams of locally compact spaces lcω-spaces.
Proof. Let τ” be the topology determined by the spaces (Km, τm) × (Ln, τ’n), m, n ∈ N.
For every open rectangle U × V, where U ∈ τ and V ∈ τ’, we claim that U × V is in τ”. For all m, n ∈ N, we need to show that (U × V) ∩ (Km × Ln) is open in (Km, τm) × (Ln, τ’n). This is clear since (U × V) ∩ (Km × Ln) = (U ∩ Km) × (V ∩ Ln), and U ∩ Km ∈ τm (by definition of τ), V ∩ Ln ∈ τ’n (by definition of τ’). It follows that every open subset in the product topology of τ and τ’, which is a union of such open rectangles U × V, is in τ”.
The harder part consists in showing that every set W in τ” is open in the product topology of τ and τ’. Let (x, y) be any point in W. We wish to find an open rectangle (for the product topology) that contains (x, y) and is contained in W. Since ∪n ∈ N Kn = X and ∪n ∈ N Ln = Y, there is a natural number n such that x is in Kn and y is in Ln. By definition of τ”, W ∩ (Kn × Ln) is open in (Kn, τn) × (Ln, τ’n), so there is an open set Un ∈ τn and there is an open set Vn ∈ τ’n such that (x, y) ∈ Un × Vn ⊆ W ∩ (Kn × Ln).
Since (Kn, τn) and (Ln, τ’n) are locally compact, there is a compact saturated neighborhood Qn of x in (Kn, τn) that is included in Un. We write U’n for the interior of Qn in (Kn, τn). Similarly, there is a compact saturated neighborhood Rn of y in (Ln, τ’n) that is included in Vn. We write V’n for the interior of Rn in (Ln, τ’n).
The situation for now can be described as in the picture below. I have shown Un × Vn, U’n × V’n, and the red rectangle is a depiction of Qn × Rn.
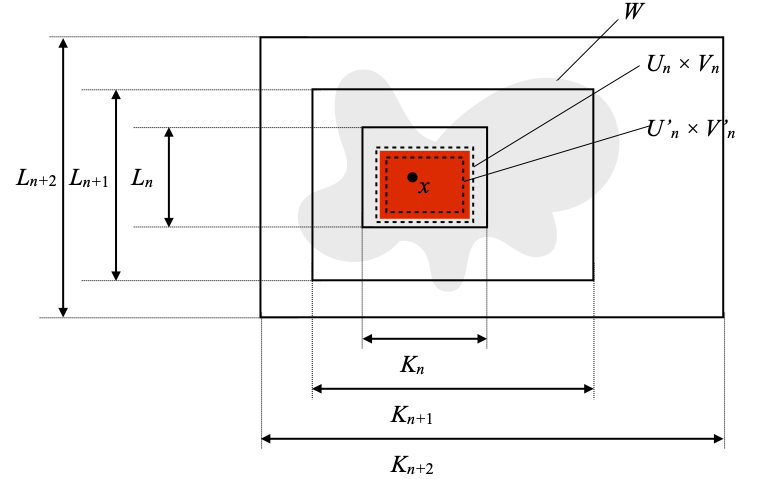
The nice thing about compact subsets is that their direct image by continuous maps is compact, in contract to the fact that the inverse images of open subsets are open. This allows us to push forward our constructions to the spaces at index n+1. Explicitly, the image (in × jn) [Qn × Rn] is compact in (Kn+1, τn+1) × (Ln+1, τ’n+1). As a set of points, that image is just Qn × Rn, but it is important to note that that in going to (Kn+1, τn+1) × (Ln+1, τ’n+1), we have changed topologies.
Since Qn ⊆ Un, Rn ⊆ Vn, and Un × Vn ⊆ W ∩ (Kn × Ln), we also have that (in × jn) [Qn × Rn] (= Qn × Rn, as a set of points) is included in W ∩ (Kn+1 × Ln+1). Now (in × jn) [Qn × Rn] is a product of compact subsets in Kn+1 × Ln+1, and W ∩ (Kn+1 × Ln+1) is an open neighborhood of it, in (Kn+1, τn+1) × (Ln+1, τ’n+1). We can therefore use Wallace’s theorem and find an open neighborhood Un+1 of Qn in (Kn+1, τn+1) and an open neighborhood Vn+1 of Rn in (Ln+1, τ’n+1) such that Un+1 × Vn+1 ⊆ W ∩ (Kn+1 × Ln+1).
By the interpolation property in locally compact spaces (Proposition 4.8.14 in the book), we can find a compact (saturated) subset Qn+1 of (Kn+1, τn+1) such that Qn ⊆ U’n+1 ⊆ Qn+1 ⊆ Un+1, where U’n+1 is the interior of Qn+1 in (Kn+1, τn+1). Similarly, we can find a compact (saturated) subset Rn+1 of (Ln+1, τ’n+1) such that Rn ⊆ V’n+1 ⊆ Rn+1 ⊆ Vn+1, where V’n+1 is the interior of Rn+1 in (Ln+1, τn+1). (I am a bit insistent on which spaces you take compact subsets or interiors in, because that is important.)
The situation is now as follows. I have removed Un × Vn, in order to reduce visual clutter, and since those are not the important open rectangles. We have pushed forward Qn × Rn through in × jn into the larger space Kn+1 × Ln+1, and that still appears graphically as the same red region, except that it should now be understood as a region in Kn+1 × Ln+1. We then obtain Un+1 × Vn+1, which I have not shown, then U’n+1 × V’n+1, and finally Qn+1 × Rn+1, pictured as the orange region.
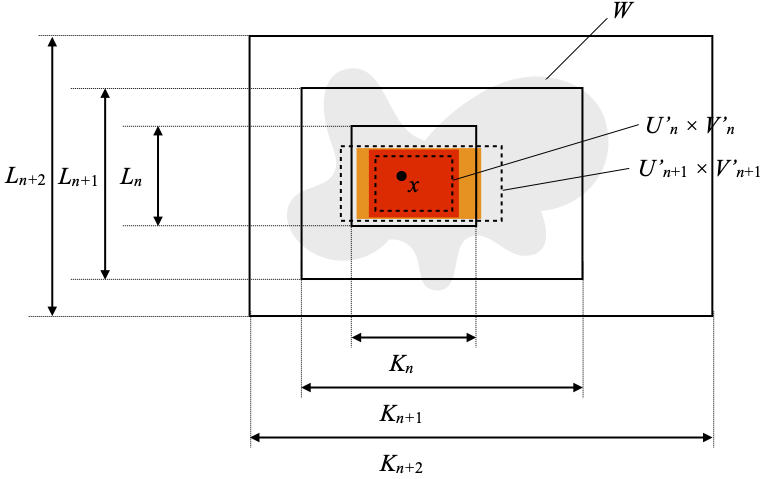
We continue in the same way at the following stages n+2, n+3, etc. Let me do it explicitly at stage n+2.
Since Qn+1 ⊆ Un+1, Rn+1 ⊆ Vn+1, and Un+1 × Vn+1 ⊆ W ∩ (Kn+1 × Ln+1), we also have that (in+1 × jn+1) [Qn+1 × Rn+1] (= Qn+1 × Rn+1, as a set of points) is included in W ∩ (Kn+2 × Ln+2). Now (in+1 × jn+1) [Qn+1 × Rn+1] is a product of compact subsets in Kn+2 × Ln+2, and W ∩ (Kn+2 × Ln+2) is an open neighborhood of it, in (Kn+2, τn+2) × (Ln+2, τ’n+2). We can therefore use Wallace’s theorem and find an open neighborhood Un+2 of Qn+1 in (Kn+2, τn+2) and an open neighborhood Vn+2 of Rn+1 in (Ln+2, τ’n+2) such that Un+2 × Vn+2 ⊆ W ∩ (Kn+2 × Ln+2).
By the interpolation property in locally compact spaces (Proposition 4.8.14 in the book), we can find a compact (saturated) subset Qn+2 of (Kn+2, τn+2) such that Qn+1 ⊆ U’n+2 ⊆ Qn+2 ⊆ Un+2, where U’n+2 is the interior of Qn+2 in (Kn+2, τn+2). Similarly, we can find a compact (saturated) subset Rn+2 of (Ln+2, τ’n+2) such that Rn+1 ⊆ V’n+2 ⊆ Rn+2 ⊆ Vn+2, where V’n+2 is the interior of Rn+2 in (Ln+2, τn+2).
And so on, and so forth, at stages n+3, n+4, etc. Note that x ∈ U’n ⊆ Qn ⊆ U’n+1 ⊆ Qn+1 ⊆ U’n+2 ⊆ Qn+2 ⊆ … and y ∈ V’n ⊆ Rn ⊆ V’n+1 ⊆ Rn+1 ⊆ V’n+2 ⊆ Rn+2 ⊆ … Also, U’n+k ⊆ Qn+k ⊆ Un+k and V’n+k ⊆ Rn+k ⊆ Vn+k for every k ∈ N. Finally, Un+k × Vn+k ⊆ W ∩ (Kn+k × Ln+k) for every k ∈ N.
Let U ≝ ∪k ∈ N U’n+k and V ≝ ∪k ∈ N V’n+k. We have the following properties:
- x ∈ U and y ∈ V: because (x, y) ∈ U’n × V’n;
- U’n ⊆ U’n+1 ⊆ … ⊆ U’n+k ⊆ … (because U’n ⊆ Qn ⊆ U’n+1 ⊆ Qn+1 ⊆ U’n+2 ⊆ Qn+2 ⊆ …) and V’n ⊆ V’n+1 ⊆ … ⊆ V’n+k ⊆ … (because V’n ⊆ Rn ⊆ V’n+1 ⊆ Rn+1 ⊆ V’n+2 ⊆ Rn+2 ⊆ …);
- U × V ⊆ W: every pair in U × V is in U’n+k × V’n+k for k large enough, hence in Un+k × Vn+k (since U’n+k ⊆ Qn+k ⊆ Un+k and V’n+k ⊆ Rn+k ⊆ Vn+k), hence in W, since Un+k × Vn+k ⊆ W ∩ (Kn+k × Ln+k);
- U is in τ. It suffices to show that U ∩ Km is open in (Km, τm) for every m ∈ N. Now U ∩ Km = ∪k ∈ N (U’n+k ∩ Km). But the sequence of sets U’n+k is monotone (U’n ⊆ U’n+1 ⊆ … ⊆ U’n+k ⊆ …), so U ∩ Km is also equal to ∪k ∈ N, n+k≥m (U’n+k ∩ Km). For every k such that n+k≥m, U’n+k ∩ Km = im–1(im+1–1(… in+k–1–1(U’n+k))) is open in (Km, τm), since the maps im, im+1, …, in–1 are continuous and U’n+k ∈ τn+k. Therefore U ∩ Km = ∪k ∈ N, n+k≥m (U’n+k ∩ Km) is a union of sets in τm, hence is itself in τm.
- V is in τ’: this relies on a similar argument.
And that’s it. We have found an open rectangle U × V containing (x, y) and included in W, where U ∈ τ and V ∈ τ’. Since (x, y) is arbitrary in W, W is open in the product topology of τ and τ’. Since W is an arbitrary element of τ”, τ” is included in the product of the topologies τ and τ’. We had shown the reverse inclusion at the beginning of the proof, so τ” coincides with the product topology of τ and τ’. ☐
From colimits of locally compact spaces to colimits of core-compact spaces
As I said, we can improve slightly on Lawson and Xu’s Theorem E, by requiring core-compactness instead of local compactness. The proof is essentially the same, replacing compact (saturated) subsets by Scott-open filters of open subsets, through the Hofmann-Mislove theorem (see below). The price is that the proof will be less readable. But I’ll make it almost a copy-and-pasted version of the previous proof, so that you can compare.
Before we start, let me recall that Examples A—D should convince you that we should not be able to relax the assumptions of Theorem E much more.
Let us write OX for the lattice of open subsets of a space X, and FL for the collection of filters of a bounded lattice L. Let me remind you that a filter on L is a collection of elements of L that contains the top element ⊤ of L, that is upwards-closed, and that is closed under finite infima. I will also write ΦL for the subfamily of Scott-open filters on L. Hence FOX is the collection of all filters of open subsets of X, and ΦOX is the collection of Scott-open filters of open subsets of X.
The Hofmann-Mislove theorem (Theorem 8.3.2 in the book) states that there is a bijective correspondence between ΦOX and QX, the collection of compact saturated subsets of X, provided that X is sober. In one direction, the collection of open neighborhoods of any compact saturated subset Q of X is always a Scott-open filter of open subsets of X, even if X is not sober. In the other direction, if X is sober, then given any F ∈ ΦOX, the intersection of all the open sets in F is a compact saturated set Q, and F is exactly its set of open neighborhoods.
Given any continuous map f : X → Y, the direct image f[Q] of any compact subset Q of X is compact. Similarly, we write f[F] for the (direct) image of a filter F ∈ FOX, defined as {V ∈ OX | f–1(V) ∈ F}. This is a filter of open sets, which is Scott-open if F is.
Imitating the product of compact (saturated) sets, we define the following product operation on filters of open sets: given any two spaces X and Y, and any filters F ∈ FOX, G ∈ FOY, we write F ⊗ G for the smallest filter on O(X × Y) that contains all the open rectangles U × V with U ∈ F and V ∈ G. The following is then both a variant of Tychonoff’s theorem (in its binary form: the product of any two compact subsets is compact), and a variant of Wallace’s theorem.
Proposition F (à la Wallace-Tychonoff). For any two Scott-open filters F ∈ ΦOX, G ∈ ΦOY, F ⊗ G is in ΦO(X × Y).
Proof. Let SX be the sobrification of X, and similarly with SY. (See Section 8.2 in the book for the theory of sober spaces and sobrifications.) SX is the set of all irreducible closed subsets of X, namely the non-empty closed subsets C of X such that, whenever C is included in the union of two closed sets, then C is included in at least one of them. The topology of SX consists exactly of the sets ♢U ≝ {C ∈ SX | C intersects U}, where U ranges over OX, and then ♢ : U ↦ ♢U is an order-isomorphism between OX and OSX. There is a continuous map η : X → SX defined by η(x) ≝ ↓x for every x ∈ X. (This is even a topological embedding if X is T0.) We will also write η for the similarly defined map from Y to SY. Finally, the sobrification (here SX and SY) of any space is sober.
Let η[F] be the image of of F under η, namely the Scott-open filter of open subsets ♢U of SX such that U is in F. We build η[G] similarly. Since SX and SY are sober, we may use the Hofmann-Mislove theorem: there are compact saturated subsets Q of SX and R of SY such that η[F] = {♢U ∈ OSX | Q ⊆ ♢U} and η[G] = {♢V ∈ OSY | R ⊆ ♢V}. Hence, for every open subset U of X, U ∈ F if and only if Q ⊆ ♢U, and for every open subset V of Y, V ∈ G if and only if R ⊆ ♢V.
By Theorem 8.4.8 in the book, there is a homeomorphism Π : SX × SY → S(X × Y) defined by Π(C, C’) ≝ C × C’. We have Π–1(♢(U × V)) = ♢U × ♢V for every open subset U of X and for every open subset V of Y.
It is clear that F ⊗ G is a filter of open sets. Let W be an open subset of X × Y that is in F ⊗ G, and let us assume that W is the union of a directed family (Wi)i ∈ I of open subsets of X × Y. We wish to show that some Wi is in F ⊗ G. By definition, W contains an open rectangle U × V with U ∈ F and V ∈ G. Then ♢W contains ♢(U × V), hence Π–1(♢W) contains ♢U × ♢V. Since U ∈ F, Q ⊆ ♢U, and since V ∈ G, R ⊆ ♢V. Hence Q × R ⊆ ♢U × ♢V ⊆ Π–1(♢W). Since both ♢ and Π–1 commute with arbitrary unions, and since Q × R is compact (by the binary Tychonoff theorem), Q × R ⊆ Π–1(♢Wi) for some i ∈ I. By Wallace’s theorem, we can find open neighborhoods ♢U’ of Q in SX and ♢V’ of R in SY (equivalently, satisfying U’ ∈ F and V’ ∈ G) such that ♢U’ × ♢V’ ⊆ Π–1(♢Wi). Since Π is a bijection and Π–1(♢(U’ × V’)) = ♢U’ × ♢V’, we obtain that U’ × V’ ⊆ Wi. Therefore Wi is in F ⊗ G. ☐
Proposition G. Given any two continuous maps f : X → Z and g : Y → T, for all Scott-open filters F ∈ ΦOX and G ∈ ΦOX’, (f × g) [F ⊗ G] = f[F] ⊗ g[G].
Proof. The elements of f[F] ⊗ g[G] are the open subsets W’ of Z × T that contain an open rectangle U’ × V’ such that f–1(U’) ∈ F and g–1(V’) ∈ G. Each of them is such that (f × g)–1(W’) contains f–1(U’) × g–1(V’), hence is in F ⊗ G. Therefore W’ is in (f × g) [F ⊗ G]. This shows that f[F] ⊗ g[G] is included in (f × g) [F ⊗ G].
In the reverse direction, we use the sobrification trick, as in the proof of Proposition F. We use the same notations: there is a compact saturated subset Q of SX such that the open subsets U of X that are in F are exactly those such that Q ⊆ ♢U, and there is a compact saturated subset R of SY such that the open subsets V of Y that are in G are exactly those such that R ⊆ ♢V. We will also use the fact that S is a functor (Lemma 8.2.42 in the book): there is a continuous map Sf : SX → SY, defined as mapping every irreducible closed subset C of X to cl(f[C]) (where f[C] is the direct image of C under f), (Sf)–1(♢U) = ♢f–1(U), and (Sf) o η = η o f; similarly with g.
Let W’ be any open subset of Z × T that is in (f × g) [F ⊗ G]: (f × g)–1(W’) contains an open rectangle U × V with U ∈ F and V ∈ G. In particular, Q × R ⊆ ♢U × ♢V. Using the homeomorphism Π : SZ × ST → S(Z × T), it follows that Π[Q × R] = {C × D | C ∈ Q, D ∈ R} is included in Π[♢U × ♢V] = ♢(U × V), hence in ♢(f × g)–1(W’). In other words, for every C ∈ Q and for every D ∈ R, C × D intersects (f × g)–1(W’); hence there is a point x in C and a point y in D such that (f(x), g(y)) ∈ W’; so S(f)(C) × S(g)(D) intersects W’, or equivalently, is in ♢W’. Using the inverse of Π, the pair (S(f)(C), S(g)(D)) is in Π–1(♢W’). Since this holds for every C ∈ Q and for every D ∈ R, S(f)[Q] × S(g)[Q’] ⊆ Π–1(♢W’).
We use Wallace’s theorem: there is an open subset U’ of Z and an open subset V’ of T such that Sf[Q] × Sg[R] ⊆ ♢U’ × ♢V’ ⊆ Π–1(♢W’). From Sf[Q] ⊆ ♢U’, we obtain that Q ⊆ (Sf)–1(♢U’) = ♢f–1(U’), hence that f–1(U’) is in F. Similarly, g–1(V’) is in G. It remains to see that W’ contains U’ × V’. For every pair (x, x’) in U’ × V’, (↓x, ↓x’) is in ♢U’ × ♢V’, hence in Π–1(♢W’); therefore ↓x × ↓x’ intersects W’; but ↓x × ↓x’ = ↓(x, x’), and since W’ is upwards-closed, (x, x’) is in W’. To sum up, W’ contains U’ × V’, f–1(U’) is in F, g–1(V’) is in G, so W’ is in f[F] ⊗ g[G]. ☐
We also need an analogue of the interpolation theorem for locally compact spaces, which would adapt to filters and core-compact spaces.
Lemma H. Let X be a core-compact space. For every Scott-open filter F ∈ ΦOX, for every U ∈ F, there is an element U’ ∈ F and a Scott-open filter F‘ ∈ ΦOX such that:
- U ∈ F’;
- U’ is included in every element of F’.
(Think of F and F’ as the collection of open neighborhoods of compact saturated sets Q and Q’ respectively. Q and Q’ will only exist in the sobrification of X, but if you overlook this for a moment, then we start from Q ⊆ U, and Lemma H gives us U’ and Q’ satisfying U’ ∈ F and conditions 1 and 2, equivalently Q ⊆ U’ ⊆ Q’ ⊆ U.)
Proof. Since X is core-compact, its sobrification SX is locally compact. Indeed, SX is core-compact, since core-compactness means that the lattice of open sets is continuous, and a space and its sobrification have order-isomorphic lattices of open subsets (through ♢ : U ↦ ♢U); and any sober, core-compact space is locally compact (see Theorem 8.3.10 in the book).
Writing η for the map z ↦ ↓z as in the proof of Proposition F, there is a compact saturated neighborhood Q of η(x) in SX that is included in ♢U. We write ♢U’ for the interior of Q in SX. Then F’ ≝ {U ∈ OX | Q ⊆ ♢U} is a Scott-open filter of open subsets of X, since F’ is isomorphic to the Scott-open filter of open neighborhoods of Q through ♢; U is in F’, and U’ is included in every element of F. ☐
And here is the promised improvement of Lawson and Xu’s theorem E.
Theorem I. Let F, G : N → Top be two ω-rigid diagrams, where each space F(n) and each space G(n) is core-compact. Then colim (F × G) = colim F × colim G.
As with Theorem E, the setup is the following. We are given a monotone sequence K0 ⊆ K1 ⊆ … ⊆ Kn ⊆ … of subsets Kn (n ∈ N) of a common set X, with ∪n ∈ N Kn = X, each with a topology τn that makes Kn core-compact, and the inclusion map in : (Kn, τn) → (Kn+1, τn+1) is continuous for every n ∈ N; namely, for every open subset U of (Kn+1, τn+1), U ∩ Kn is open in (Kn, τn). We also have a monotone sequence L0 ⊆ L1 ⊆ … ⊆ Ln ⊆ … of subsets Ln (n ∈ N) of a common set Y, with ∪n ∈ N Ln = Y, a topology τ’n on Ln that makes it core-compact, and the inclusion map jn : (Ln, τ’n) → (Ln+1, τ’n+1) is continuous for every n ∈ N; namely, for every open subset V of (Ln+1, τ’n+1), V ∩ Ln is open in (Ln, τ’n).
Then the theorem claims that the topology determined by the spaces (Km, τm) × (Ln, τ’n), where m, n ∈ N, coincides with the product topology on (X, τ) × (Y, τ’), where τ is the topology determined by the spaces (Km, τm) and τ’ is the topology determined by the spaces (Ln, τ’n).
Proof. Let τ” be the topology determined by the spaces (Km, τm) × (Ln, τ’n), m, n ∈ N.
For every open rectangle U × V, where U ∈ τ and V ∈ τ’, we claim that U × V is in τ”. For all m, n ∈ N, we need to show that (U × V) ∩ (Km × Ln) is open in (Km, τm) × (Ln, τ’n). This is clear since (U × V) ∩ (Km × Ln) = (U ∩ Km) × (V ∩ Ln), and U ∩ Km ∈ τm (by definition of τ), V ∩ Ln ∈ τ’n (by definition of τ’). It follows that every open subset in the product topology of τ and τ’, which is a union of such open rectangles U × V, is in τ”.
The harder part consists in showing that every set W in τ” is open in the product topology of τ and τ’. Let (x, y) be any point in W. We wish to find an open rectangle (for the product topology) that contains (x, y) and is contained in W. Since ∪n ∈ N Kn = X and ∪n ∈ N Ln = Y, there is a natural number n such that x is in Kn and y is in Ln. By definition of τ”, W ∩ (Kn × Ln) is open in (Kn, τn) × (Ln, τ’n), so there is an open set Un ∈ τn and there is an open set Vn ∈ τ’n such that (x, y) ∈ Un × Vn ⊆ W ∩ (Kn × Ln).
Since (Kn, τn) and (Ln, τ’n) are core-compact, we can use the interpolation Lemma H, with the (Scott-open) filter of open neighborhoods of x in (Kn, τn) for F, and we obtain an element U’n (the U’ of the lemma) of F, namely an open neighborhood U’n of x in (Kn, τn), and a Scott-open filter Fn of open subsets of (Kn, τn) (the F’ of Lemma H) such that: 1. Un is in Fn, and 2. U’n is included in every element of Fn.
Similarly, there is a Scott-open filter Gn of open subsets of (Ln, τ’n) that contains Vn, and an open neighborhood V’n of y in (Ln, τ’n) that is included in every element of Gn.
The situation for now can be described as in the picture below. I have shown Un × Vn, U’n × V’n, and the red rectangle is a brief depiction of Fn ⊗ Gn: Fn ⊗ Gn is given by a product of two compact saturated subsets in the sobrification of Kn × Ln, and the red rectangle denotes that product of compact subsets. In other words, the elements of Fn ⊗ Gn are the open subsets of Kn × Ln that contain the red rectangle.

By Propositions F and G, (in × jn) [Fn ⊗ Gn] = in[Fn] ⊗ jn[Gn] is a Scott-open filter of open subsets of (Kn+1, τn+1) × (Ln+1, τ’n+1). Also, W ∩ (Kn+1 × Ln+1) is in (in × jn) [Fn ⊗ Gn], since (in × jn)–1(W ∩ (Kn+1 × Ln+1)) = W ∩ (Kn × Ln) contains Un × Vn, and Un ∈ Fn and Vn ∈ Gn. Therefore W ∩ (Kn+1 × Ln+1) is in in[Fn] ⊗ jn[Gn], meaning that there are open sets Un+1 ∈ τn+1 and Vn+1 ∈ τ’n+1 such that Un+1 × Vn+1 ⊆ W ∩ (Kn+1 × Ln+1), Un+1 ∈ in[Fn] and Vn+1 ∈ jn[Gn].
Since (Kn+1, τn+1) and (Ln+1, τ’n+1) are core-compact, we can use Lemma H. There is a Scott-open filter Fn+1 of open subsets of (Kn+1, τn+1) such that Un+1 ∈ Fn+1 and there is an element U’n+1 of in[Fn] that is included in every element of Fn+1. Similarly, there is a Scott-open filter Gn+1 of open subsets of (Ln+1, τ’n+1) that contains Vn+1, and an element V’n+1 of jn[Gn] that is included in every element of Gn+1.
Since U’n+1 ∈ in[Fn], we have U’n+1 ∩ Kn ∈ Fn, and similarly, V’n+1 ∩ Ln ∈ Gn. Since U’n is included in every element of Fn, in particular, U’n ⊆ U’n+1 ∩ Kn, and similarly V’n ⊆ V’n+1 ∩ Ln.
The situation is now as follows. I have removed Un × Vn, in order to reduce visual clutter, and since those are not the important open rectangles. We have pushed forward Fn ⊗ Gn into the larger space Kn+1 × Ln+1, by building in[Fn] ⊗ jn[Gn], and that still appears graphically as the same red region, except that it should now be understood as a region in Kn+1 × Ln+1. We then obtain Un+1 × Vn+1, which I have not shown, then U’n+1 × V’n+1, and finally Fn+1 ⊗ Gn+1, pictured as the orange region.

By Propositions F and G, (in+1 × jn+1) [Fn+1 ⊗ Gn+1] = in+1[Fn+1] ⊗ jn+1[Gn+1] is a Scott-open filter of open subsets of (Kn+2, τn+2) × (Ln+2, τ’n+2). Also, W ∩ (Kn+2 × Ln+2) is in (in+1 × jn+1) [Fn+1 ⊗ Gn+1], since (in+1 × jn+1)–1(W∩ (Kn+2 × Ln+2)) = W ∩ (Kn+1 × Ln+1) contains Un+1 × Vn+1, and Un+1 ∈ Fn+1 and Vn+1 ∈ Gn+1. Therefore W ∩ (Kn+2 × Ln+2) is in in+1[Fn+1] ⊗ jn+1[Gn+1], meaning that there are open sets Un+2 ∈ τn+2 and Vn+2 ∈ τ’n+2 such that Un+2 × Vn+2 ⊆ W ∩ (Kn+2 × Ln+2), Un+2 ∈ in+1[Fn+1] and Vn+2 ∈ jn+1[Gn+1].
We continue in the same way as in the previous paragraph, building Scott-open filters Fn+k and Gn+k for every k ∈ N, and open sets Un+k ∈ Fn+k and Vn+k ∈ Gn+k such that Un+k × Vn+k ⊆ W ∩ (Kn+k × Ln+k), as well as open sets U’n+k ∈ τn+k and V’n+k ∈ τ’n+k such that U’n+k is included in every element of Fn+k, and V’n+k is included in every element of Gn+k, and therefore U’n+k ⊆ U’n+k+1 ∩ Kn+k and V’n+k ⊆ V’n+k+1 ∩ Ln+k, Un+k+1 ∈ in+k[Fn+k] and Vn+k+1 ∈ jn+k[Gn+k].
Let U ≝ ∪k ∈ N U’n+k and V ≝ ∪k ∈ N V’n+k. We have the following properties:
- x ∈ U and y ∈ V: because (x, y) ∈ U’n × V’n;
- U’n ⊆ U’n+1 ⊆ … ⊆ U’n+k ⊆ … (because U’n+k ⊆ U’n+k+1 ∩ Kn+k for every k ∈ N) and V’n ⊆ V’n+1 ⊆ … ⊆ V’n+k ⊆ … (because V’n+k ⊆ V’n+k+1 ∩ Ln+k for every k ∈ N);
- U × V ⊆ W: every pair in U × V is in U’n+k × V’n+k for k large enough, hence in Un+k × Vn+k (remember that U’n+k is included in every element of Fn+k, in particular in Un+k, and similarly V’n+k is included in Vn+k), hence in W, since Un+k × Vn+k ⊆ W ∩ (Kn+k × Ln+k);
- U is in τ. It suffices to show that U ∩ Km is open in (Km, τm) for every m ∈ N. Now U ∩ Km = ∪k ∈ N (U’n+k ∩ Km). But the sequence of sets U’n+k is monotone (U’n ⊆ U’n+1 ⊆ … ⊆ U’n+k ⊆ …), so U ∩ Km is also equal to ∪k ∈ N, n+k≥m (U’n+k ∩ Km). For every k such that n+k≥m, U’n+k ∩ Km = im–1(im+1–1(… in+k–1–1(U’n+k))) is open in (Km, τm), since the maps im, im+1, …, in–1 are continuous and U’n+k ∈ τn+k. Therefore U ∩ Km = ∪k ∈ N, n+k≥m (U’n+k ∩ Km) is a union of sets in τm, hence is itself in τm.
- V is in τ’: this relies on a similar argument.
And that’s it. We have found an open rectangle U × V containing (x, y) and included in W, where U ∈ τ and V ∈ τ’. Since (x, y) is arbitrary in W, W is open in the product topology of τ and τ’. Since W is an arbitrary element of τ”, τ” is included in the product of the topologies τ and τ’. We had shown the reverse inclusion at the beginning of the proof, so τ” coincides with the product topology of τ and τ’. ☐
- Jimmie Lawson and Xiaoquan Xu. Spaces determined by countably many locally compact subspaces. Topology and its Applications, 354, 108973, 2024.
- Francis Borceux. Handbook of categorical algebra, vol.1.

— Jean Goubault-Larrecq (August 20th, 2024)
