Characterizing non-ω-well-filtered spaces by forbidden subspaces

In 2018, Matthew de Brecht showed that a co-analytic subset of a quasi-Polish space is either quasi-Polish or else contains a countable Π⁰₂ subset homeomorphic to one of the following four spaces:

• S₀, a space I have already talked about in the January 2023 post, and which is a countably branching tree with countable branches extending from top to bottom;
• S₁, which is simply N with the cofinite topology;
• S₂, which is simply the space Q of rational numbers;
• S_D, which is N with the Alexandroff topology of its ordering.

The names that de Brecht chose are meant to match their separation properties: S₀ is T₀, but nothing more, S₁ is T₁, S₂ is T₂, and S_D is T_D. Don’t worry about “co-analytic” or “Π⁰₂” for now. The point is essentially to characterize quasi-Polishness by excluding just 4 specific subspaces.

I have long planned to explain how this works, but this is pretty technical and long. However, there is something simpler I can explain. In [1, Theorem 4.3], de Brecht proved that a second-countable T₀ space is sober if and only if it does not contain a Π⁰₂ subspace homeomorphic to S₁ or of S_D. The proof involves looking at perfect subspaces, T_D subspaces, and so on. This result was improved upon by Qingguo Li, Mengjie Jin, Hualin Miao, and Shong Chen [2, Section 3], who showed that first-countability was enough, instead of second-countability. Then Hualin Miao, Xiaodong Jia, Ao Shen and Qingguo Li showed that one can characterize those T₀ spaces that are not ω-well-filtered as those that do not contain either S₁ or S_D as Skula-closed subspaces [3]. All that is based on de Brecht’s results and techniques, but seems easier to explain… unless you realize that the proof use some of de Brecht’s technical lemmas.

While the proofs I will give start out by following the same path as in [2], I will then fork and use more elementary (you won’t need to learn any auxiliary theorems, I will state everything that you need) and hopefully simpler arguments, although we will need to talk about Skula-closed subspaces and then ω-Rudin sets at some point, and this will start being complex again.

ω-well-filtered spaces

A space X is well-filtered if and only if given any filtered family (Q_i)_{i ∈ I} of compact saturated subsets whose intersection is included in some open subset U, some Q_i is already included in U. Every sober space is well-filtered (Proposition 8.3.5 in the book).

A refinement of this is ω-well-filtered spaces, see the October 2019 post: X is ω-well-filtered if and only if given any descending sequence Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … of compact saturated subsets whose intersection is included in some open subset U, some Q_n is already included in U.

In the list of spaces I have given at the beginning of this post:

• S₀ is sober (see the January 2023 post), hence it is well-filtered, and in particular an ω-well-filtered space.
• The space S₂ is Hausdorff (or T₂), and every Hausdorff space is sober (Proposition 8.2.12 in the book), hence well-filtered, hence ω-well-filtered space.
• The space S₁, which is just N with the cofinite topology, is not ω-well-filtered.
  Here is why. In the cofinite topology, the proper closed subsets are the finite subsets, so every descending sequence of closed sets stabilizes; by taking complements, ascending sequences of open sets stabilize, so S₁ is a Noetherian space (Proposition 9.7.6 in the book). In a Noetherian space, every subspace is compact.
  In S₁, which is T₁, therefore, every subset is even compact saturated. We let Q_n ≝ {n, n+1, …} for each n ∈ N, and those are therefore vacuously compact saturated. We let U be empty: ∩_{n ∈ N} Q_n is empty, hence included in U, but no Q_n is included in U.
  Therefore S₁ is not ω-well-filtered.
• The space S_D, which is just N with the Alexandroff topology of its usual ordering ≤, namely whose open subsets are the empty set and the sets ↑n = {n, n+1, …}, is not ω-well-filtered.
  Indeed, Q_n ≝ ↑n is just open, but also compact saturated, and as above, taking U to be empty leads to a case where ∩_{n ∈ N} Q_n ⊆ U but no Q_n is included in U.

What must happen in a non-ω-well-filtered space

In the following, we consider a non-ω-well-filtered T₀ space X, and we will see what emerges—in short, we will find homeomorphic copies of S₁ or of S_D sitting as subspaces of X. Later on, we will see that they must be Skula-closed, too.

By definition of ω-well-filteredness, there is a descending sequence Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … of compact saturated subsets of X and there is an open subset U of X such that ∩_{n ∈ N} Q_n ⊆ U but: (*) no Q_n is included in U.

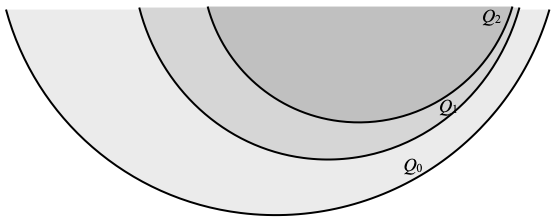
We fix the sequence Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … but will make U vary. The collection F of open sets U satisfying property (*) is a non-empty dcpo under inclusion. Indeed, it is non-empty by assumption. In order to show that F is a dcpo, we consider an arbitrary directed family (U_i)_{i ∈ I} of open subsets of X that satisfy property (*). If some Q_n were included in ∪_{i ∈ I} U_i, then it would be included in some U_i, since Q_n is compact (see Proposition 4.4.7 in the book), and that is impossible since U_i satisfies property (*). Hence ∪_{i ∈ I} U_i is in F, and F is a dcpo.
In particular, F is an inductive poset. By Zorn’s Lemma (Theorem 2.4.2 in the book), it has a maximal element U₀ above any chosen element U. By assumption, we can choose that element U so that not only property (*) is satisfied, but also ∩_{n ∈ N} Q_n ⊆ U. Hence also ∩_{n ∈ N} Q_n ⊆ U₀.

Let C₀ be the complement of U₀ in X. C₀ is a closed set. By definition, C₀ is a minimal closed set that intersects every Q_n (rephrasing property (*)), while ∩_{n ∈ N} Q_n does not intersect C₀. Since C₀ intersects every Q_n, we can pick an element x_n that is both in C₀ and in Q_n for each n ∈ N. Hence here is what our working assumption—that X is not ω-well-filtered space—boils down to.

Setting. X is a non-ω-well-filtered T₀ space, Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … is a decreasing sequence of compact saturated subsets of X, C₀ is a minimal closed set that intersects every Q_n, while ∩_{n ∈ N} Q_n does not intersect C₀, and x_n ∈ C₀ ⋂ Q_n for every n ∈ N. We also let H ≝ {x_n | n ∈ N}.

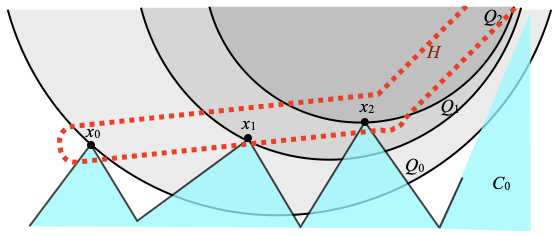
We equip C₀ and H with the subspace topology induced from the inclusion in X. The following Lemmas A and B are part of the proof of Lemma 3.2 in [3].

Lemma A. In the Setting, C₀ is equal to the closure cl (H) and H is infinite.

Proof. The closure cl (H) of H is closed, included in C₀, and intersects every Q_n (at x_n). By minimality of C₀, it must be equal to C₀.

Let us assume that H is finite. Since ∩_{n ∈ N} Q_n does not intersect C₀, hence does not intersect H either, every point y of H is outside Q_ny for some n_y ∈ N. Taking n larger than every index n_y, which is possible since H is finite, H is disjoint from Q_n; and this is impossible, since x_n is in both. Therefore H is infinite. ☐

Lemma B. In the Setting, every proper closed subset of C₀ intersets H at only finitely many points.

Proof. Let C be a closed subset of C₀ such that C ∩ H is infinite. We will show that C must be equal to the whole of C₀, contradicting the fact that it is a proper subset of C₀. Since C ∩ H is infinite, there are infinitely many indices n ∈ N such that x_n is in C. Then C intersects Q_n, and because Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n, C must intersect Q₀, Q₁, …, Q_n; and this for infinitely many values of n, hence for n arbitrarily large. It follows that C intersects every Q_n. By minimality of C₀, we must have C = C₀. ☐

As a subspace of X, H has a specialization preordering, which happens to be the restriction of the specialization ordering ≤ on X (Proposition 4.9.5 in the book). We continue to write it as ≤.

Lemma C. In the Setting, if there is a point of H that is not below any maximal point of H, then H has a subspace H’ that is homeomorphic to S_D and such that cl (H’) = C₀.

Proof. Let x_n0 be a point of H that is not below any maximal point of H. There must be another point x_n1 of H such that x_n0 < x_n1, otherwise x_n0 itself would be maximal. Also, x_n1 is not below any maximal point of H: if x_n1 were below some maximal point y, then x_n0 would be, too. Proceeding with x_n1 as we did with x_n0, there is another point x_n2 of H such that x_n1 < x_n2 and x_n2 is below no maximal point of H, and so on.

Let H’ be {x_n0, x_n1, …, x_nk, …} and C’ be its closure in X. Then C’ is included in C₀, is closed in C₀, and its intersection with H contains H’, which is infinite. Using Lemma B, C’ cannot be a proper subset of C₀, so C’ = C₀. In other words, cl (H’) = C₀.

The important point is that there is a unique topology on H’ that has ≤ as its specialization ordering. This is proved as follows. For every open subset V of H’ in the Alexandroff topology of ≤, i.e., for every upwards-closed subset V of H’, V is either empty or has a unique least element y, because H’ is well-founded. If V is empty, then it is open in any topology. Otherwise, V = ↑y. If y is the least element x_n0 of H’, then V is the whole of H’, which is also open in any topology. Otherwise, y = x_nk+1 for some k ∈ N, and then V is the complement of ↓x_nk; therefore V is open in the upper topology, which is the topology generated by the complements of downward closures of points. It follows that the Alexandroff topology is coarser than the upper topology. It is also finer, trivially, so the two topologies coincide. We conclude by Exercise 4.2.14 in the book, which states that on a preordered set, there is a unique topology that has the given preordering as its specialization preordering if and only if the Alexandroff and upper topologies coincide.

This entails that the topology of H’ is the Alexandroff topology of ≤ (also its upper topology, and also its Scott topology, etc., but that does not matter at this point).

The map f : k ↦ x_nk is a strictly monotonic bijection of N onto H’, by construction. (By strictly monotonic, we mean that k<k’ implies f(k)<f(k’).) Hence its inverse is also strictly monotonic. We remember that S_D is simply N, with the Alexandroff topology of its ordering ≤. A function between posets is monotonic if and only if it is continuous with respect to the corresponding Alexandroff topologies (Exercise 4.3.10 in the book), so f is a homeomorphism. ☐

Lemma D. In the Setting, and if every point of H is below some maximal point, then H has a subspace H’ that is homeomorphic to S₁ and such that cl (H’) = C₀.

Proof. Let Max H be the subset of maximal points of H. The assumption that every point of H is below some maximal point is equivalent to the fact that H is equal to the downward closure of Max H in H, namely to ↓Max H ⋂ H.

For every point y of Max H, ↓y is included in C₀, and is closed. It cannot be that ↓y = C₀: otherwise y would be equal to every x_n, hence would be in every Q_n, and it would also be in C₀, contradicting the fact that ∩_{n ∈ N} Q_n and C₀ are disjoint (see Setting). Hence ↓y is a proper closed subset of C₀, and therefore contains only finitely many points of H by Lemma B.

If Max H were finite, then H = ↓Max H ⋂ H would be equal to the union of the finite sets ↓y ⋂ H over the finitely many elements y of Max H, hence would be finite. This directly contradicts Lemma A: so Max H is infinite. It is also countable, because it is included in the countable set H, so there is a bijection f : N → Max H.

Every closed subset of Max H is of the form C ∩ Max H for some closed subset C of X. Replacing C by C ∩ C₀, we may assume that C is included in C₀, and is then a closed subset of C₀, seen as a subspace. By Lemma C, either C = C₀ or C contains only finitely many points in H. In other words, every closed subset of Max H is either the whole of Max H or is finite, or equivalently, every closed subset of Max H is closed in the cofinite topology on Max H.

Conversely, let us consider an arbitrary subset C’ of Max H that is closed in the cofinite topology. We claim that C’ is closed in the subspace topology induced by the inclusion in C₀ (or X).

• If C’ = Max H, then C’ is closed in Max H in the subspace topology.
• Otherwise, C’ is finite. Let C ≝ ↓C’. Being the downward closure of a finite set, C is closed in X (see Exercise 4.2.8 in the book).
  We claim that C’ = C ∩ Max H. That C’ ⊆ C ∩ Max H is clear. In the reverse direction, every point x of C ∩ Max H is below some point y of C’ ⊆ Max H; but since x and y are both maximal in H and x≤y, we must have x=y. (This is where we use the fact that X is T₀.) Then x is in C’, because y is.
  The equality C’ = C ∩ Max H shows that C’ is closed in Max H with the subspace topology.

We let H’ ≝ Max H. We have just proved that the subspace topology on H’ is the cofinite topology. Hence f is a homeomorphism from N with its own cofinite topology—namely, S₁—onto H’. ☐

Putting together Lemmas C and D, in the Setting, there is a homeomorphic copy H’ of S₁ or of S_D that sits as a subspace of the non-ω-well-filtered space X. Additionally, cl(H’) is equal to the minimal closed set C₀ intersecting every Q_n but not ∩_{n ∈ N} Q_n, which we chose initially.

This is not yet a characterization of ω-well-filtered spaces, and we need to go through Skula-closed subsets, as Miao, Jia, Shen and Li do [3].

Skula-closed subsets

I have already talked about the Skula topology several times, and notably in the August 2019 post, where we showed that for a subspace X of a sober space Z, it is equivalent for X to be sober, or to be Skula-closed. This is also mentioned in Exercise 9.7.16 of the book.

Here is a quick reminder of the definition. The Skula topology (also called the strong topology) on a topological space X is the topology generated by the open subsets and the closed subsets of X. It is equivalent to define it as the topology generated by the open subsets and the downwards-closed subsets of X. A Skula-closed subset of X is one that is closed in the Skula topology; Skula-open is defined similarly.

Lemma E. In the Setting, any countably infinite subset A of C₀ such that cl (A) = C₀ is Skula-closed in X. In particular, H is Skula-closed in X, and the subspaces H’ found in Lemma C or in Lemma D are Skula-closed in X.

Proof. Both H and H’ (whether built in Lemma C or in Lemma D) are countably infinite subsets of C₀ and their closure is equal to C₀, by Lemma A, C or D respectively. Hence it suffices to prove the first part of the lemma.

The argument is similar to one used in the proof of Lemma 3.2 of [3], except the authors write B for our H’, and H_n for what is essentially our forthcoming A_n. We write A as {y₀, y₁, …, y_n, …}, where the points y_n are pairwise distinct. For every n ∈ N, we let A_n ≝ {y₀, y₁, …, y_n} ∪ Q_n.

Since every downwards-closed subset of X is Skula-open, by taking complements we obtain that every upwards-closed subset of X is Skula-closed. In particular, Q_n is Skula-closed. Every one-point set {x} is Skula-closed, because it arises as the intersection of the closed set ↓x with the upwards-closed (hence Skula-closed) set ↑x, using the fact that X is T₀. For every n ∈ N, A_n is a finite union of Skula-closed sets, and is therefore Skula-closed.

We claim that A = (∩_{n ∈ N} A_n) ⋂ C₀.

• Every point of A is equal to y_m for some m ∈ N. We verify that y_m ∈ (∩_{n ∈ N} A_n) ⋂ C₀. By definition of y_m, y_m is in A, hence in C₀, and it remains to verify that y_m ∈ A_n for every n ∈ N. If m≤n, then y_m ∈ {y₀, y₁, …, y_n} ⊆ A_n. Otherwise, y_m is in Q_m, which is included in Q_n, hence in A_n.
  Therefore A ⊆ (∩_{n ∈ N} A_n) ⋂ C₀.
• In the reverse direction, let y be a point of (∩_{n ∈ N} A_n) ⋂ C₀. We reason by contradiction and we assume that y is not in A. This means that y is not equal to any point y₀, y₁, …, y_n, … For every n ∈ N, y is in A_n = {y₀, y₁, …, y_n} ∪ Q_n, and therefore must be in Q_n. Hence y is in ∩_{n ∈ N} Q_n. But ∩_{n ∈ N} Q_n does not intersect C₀, while y lies in C₀: contradiction.
  Therefore (∩_{n ∈ N} A_n) ⋂ C₀ ⊆ A.

The formula A = (∩_{n ∈ N} A_n) ⋂ C₀ displays A as an intersection of Skula-closed subsets of X, so A is Skula-closed. ☐

Putting together what we now know from Lemmas C, D and E, if X is not ω-well-filtered and T₀, then there is a homeomorphic copy H’ of S₁ or of S_D that sits as a Skula-closed subspace of X.

When X is first-countable, we can refine Lemma E as follows. A UCO subset (“union of closed and open”) of a topological space is a union of a closed subset and of an open subset. UCO subsets were mentioned in the March 2019 post on countably presented locales, or in the August 2019 post on sober subspaces and the Skula topology, or in the September 2025 post on compactly Choquet-complete spaces. A Π⁰₂ subset is a countable intersection of UCO subsets. Every Π⁰₂ subset is Skula-closed; in fact the Skula-closed subsets are the intersections of UCO subsets, not necessarily just countably many of them. The following is Theorem 3.4 of [3].

Lemma E’. In the Setting, and if X is also first-countable, then any countably infinite subset A of C₀ such that cl (A) = C₀ is Π⁰₂ in X. In particular, H is Π⁰₂ in X, and the subspaces H’ found in Lemma C or in Lemma D are Π⁰₂ in X.

Proof. We claim that:

• Every open subset of X, every closed subset of X is UCO, hence Π⁰₂.
• Every one-element set {x} is Π⁰₂. Since X is first-countable, x has a countable base of open neighborhoods (U_n)_{n ∈ N}, hence {x} = ↓x ⋂ ↑x = ↓x ⋂ ∩_{n ∈ N} U_n, which is Π⁰₂.
• Every finite union of Π⁰₂ subsets is Π⁰₂. It suffices to observe that finite unions of UCO subsets are UCO subsets, and to distribute countable intersections over finite unions.
• Every compact saturated subset Q is Π⁰₂. Let (U^x_n)_{n ∈ N} be a countable base of open neighborhoods of each point x of Q. Following Exercise 4.7.14 in the book, we will assume that they form a descending sequence U^x₀ ⊇ U^x₁ ⊇ … ⊇ U^x_n ⊇ …; the fact that they form a base of open neighborhoods means that every open neighborhood of x contains some U^x_n.
  For every n ∈ N, the sets U^x_n where x varies over Q form an open cover of Q. We extract a finite subcover (U^x_n)_{x ∈ An} (where each set A_n is a finite subset of Q), and we write V_n for ∪_{x ∈ An} U^x_n.
  Then Q ⊆ V_n, and we claim that Q = ∩_{n ∈ N} V_n; this will show the claim. In fact , this will even show that Q is G_δ, in other words, a countable intersection of open sets.
  Since Q is saturated, it is equal to the intersection of its open neighborhoods, so it suffices to show that every open neighborhood V of Q contains some V_n. We fix V, and for every point x of Q, we find an open neighborhood U^x_nx in the base (U^x_n)_{n ∈ N} of open neighborhoods of x that is included in V—this is by definition of a base of open neighborhoods. Since Q is compact, a finite number of such open neighborhoods U^x_nx cover Q. We take n larger than or equal to all the finitely many numbers n_x thus obtained, and then V_n ⊆ V.

We now proceed just like in the proof of Lemma E, replacing “Skula-closed” by “Π⁰₂” everywhere: A_n ≝ {y₀, y₁, …, y_n} ∪ Q_n is now Π⁰₂ for every n ∈ N, so A = (∩_{n ∈ N} A_n) ⋂ C₀ is Π⁰₂, too. ☐

We turn to the converse: showing that an ω-well-filtered space cannot contain any Skula-closed subspace homeomorphic to S₁ or to S_D.. This requires a detour through some properties of ω-well-filtered spaces and ω-Rudin sets.

Skula-closed subspaces of ω-well-filtered spaces

The characteristic feature of the set C₀ we have built and studied in previous sections is that it is a minimal closed set that intersects every element Q_n from a descending sequence of compact saturated subsets. Such sets are very much related to the following notion, due to Xiaoquan Xu, Chong Shen, Xiaoyong Xi and Dongsheng Zhao [4, Definition 5.1].

Definition. A closed subset C of a topological space X is ω-Rudin if and only if there is a descending sequence Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … of compact saturated subsets of X such that C is a minimal closed set that intersects every Q_n.

In general, an ω-Rudin subset is a subset whose closure is ω-Rudin, but we will not need that generality. The notion originally stems from the topological Rudin lemma, which we have seen in the February 2021 post.

The following is Corollary 6.11, item (2) in [4]. We note that every set of the form ↓x is closed (since it is the closure of x) and ω-Rudin: take Q_n ≝ ↑x for every n ∈ N, then Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … is a descending sequence of compact saturated subsets of X that all intersect ↓x, and every closed set C that intersects every Q_n must contain x, hence be a superset of ↓x, which shows the minimality of ↓x.

Proposition F. Let X be a topological space. Then X is ω-well-filtered if and only if every ω-Rudin closed subset of X is of the form ↓x for some point x of X.

Proof. We show that the negations of the given properties are equivalent, namely that X is not ω-well-filtered if and only if there is an ω-Rudin closed subset of X that is not of the form ↓x for any point x of X.

If X is not ω-well-filtered, then we reuse the Setting. By Lemmas C and D, there is a subspace H’ of X that is homeomorphic to S₁ or to S_D and such that cl (H’) = C₀, a minimal closed set that intersects every Q_n, and such that C₀ is disjoint from ∩_{n ∈ N} Q_n. In particular, C₀ is closed and ω-Rudin, but not of the form ↓x for any point x of X.

Conversely, let us assume that we can find an ω-Rudin closed subset C of X that is not of the form ↓x for any point x of X. By definition of an ω-Rudin set, there is a descending sequence Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … of compact saturated subsets of X such that C is a minimal closed set that intersects every Q_n. Let U be the complement of C in X. Then no Q_n is included in U.

If ∩_{n ∈ N} Q_n and C had a non-empty intersection, then we could pick a point x in that intersection, and then ↓x would be a closed subset of X that intersects every Q_n. This is impossible since ↓x is a proper subset of C, and since C is minimal. Therefore ∩_{n ∈ N} Q_n and C are disjoint. In other words, ∩_{n ∈ N} Q_n is included in U. Since no Q_n is included in U, X is not ω-well-filtered. ☐

Proposition G. Every Skula-closed subspace of an ω-well-filtered space is ω-well-filtered.

Proof. The argument is buried inside the proof of [3, Theorem 3.3]. Let X be a Skula-closed subspace of an ω-well-filtered space Y. In order to show that X is ω-well-filtered, we rely on Proposition F: we consider an arbitrary ω-Rudin closed subset C of X, and we wish to prove that C = ↓x for some point x of X. By definition, there is a descending sequence K₀ ⊇ K₁ ⊇ … ⊇ K_n ⊇ … of compact saturated subsets of X such that C is a minimal closed subset of X that intersects every K_n.

Let us write cl_Y for closure in Y, ↑_Y for upward closure in Y and ↓_Y for downward closure in Y. (We keep ↓ for downward closure in X.)

Let C’ ≝ cl_Y (C). We claim that C’ is ω-Rudin in Y.

• First, we note that C’ ⋂ X = C. The inclusion C ⊆ C’ ⋂ X is clear. Conversely, since C is closed in X, we can write C as C” ⋂ X for some closed subset C” of Y. Then C ⊆ C”, and since C” is closed in Y, cl_Y (C) ⊆ C”, in other words C’ ⊆ C”. Then C’ ⋂ X ⊆ C” ⋂ X = C.
• It is easy to see that a compact subset of X is also compact in Y, so every K_n is compact in X. We let Q_n ≝ ↑_YK_n for every n ∈ N, so Q_n is compact saturated in Y. Also, Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … is a descending sequence of compact saturated subsets of Y, and Q_n ⋂ X = K_n for every n ∈ N: the latter is because K_n is saturated in X, and the specialization preordering of X is the restriction of that of Y.
• Since C’ contains C and Q_n contains K_n for every n ∈ N, and since C intersects every K_n, C’ intersects every Q_n.
• Now let us imagine a closed subset C” of Y, included in C’ and which still intersects every Q_n. Then C” ⋂ X is closed in X, intersects every K_n, and is included in C’ ⋂ X, which is equal to C, as we have seen above. By the minimality property of C, C” ⋂ X = C. In particular, C” contains C, and since C” is closed in Y, it must also contain cl_Y (C), namely C’. But C” is included in C’, so C” = C’.
  This shows that C’ is a minimal closed subset of Y that intersects every Q_n. Hence C’ is ω-Rudin in Y, as promised.

Because Y is ω-well-filtered, by Proposition F there is a point y of Y such that C’ = ↓_Yy. Every Skula-open neighborhood O of y contains an intersection U ⋂ C” of an open subset U of Y and of a closed subset C” of Y, which both contain y, by definition of the Skula topology. This intersection contains the smaller intersection U ⋂ ↓_Yy, which is also Skula-open. We finally use the fact that X is Skula-closed in Y: if y were not in X, then we could take the complement of X in Y for the Skula-open set O, showing that there would be an open neighborhood U of y in Y such that U ⋂ ↓_Yy is included in O, namely disjoint from X. But C’ = ↓_Yy, so that would entail that U ⋂ C’ ⋂ X = ∅, equivalently that U ⋂ C = ∅; meanwhile, U intersects C’ = ↓_Yy (at y), and C’ = cl_Y (C), so U must intersect C: contradiction.

Therefore y is in X. We have C = C’ ⋂ X = ↓_Yy ⋂ X, and since y is in X, the latter is just ↓y. ☐

The main theorem

We finally arrive at the main theorem I wanted to come to [3, Theorem 3.3].

Theorem H (Miao-Jia-Shen-Li). A T₀ topological space X is ω-well-filtered if and only if it does not contain any Skula-closed subspace homeomorphic to S₁ or to S_D.
A first-countable T₀ topological space X is ω-well-filtered if and only if it does not contain any Π⁰₂ subspace homeomorphic to S₁ or to S_D.

Proof. If X is ω-well-filtered, then every Skula-closed subspace Y (in particular every Π⁰₂ subspace) of X is itself ω-well-filtered. At the beginning of this post, we have seen that S₁ and S_D are not ω-well-filtered. Hence X does not contain any Skula-closed subspace homeomorphic to S₁ or to S_D.

Conversely, if X is not ω-well-filtered and T₀ (resp. and first-countable) , we have seen in Lemmas C, D and E (resp. and E’) that there is a homeomorphic copy H’ of S₁ or of S_D that sits as a Skula-closed (resp. Π⁰₂) subspace of X. ☐

I have the hope that this could be a first step in eventually explaining de Brecht’s results on quasi-Polish spaces in [1]. We will see! In the meantime, I would like to conclude with an application to first-countable sober spaces.

First-countable sober spaces, first-countable ω-well-filtered spaces

In the first-countable case, we obtain a bit more, and we can characterize sobriety, not just ω-well-filteredness. This is due to Xiaoquan Xu, Chong Shen, Xiaoyong Xi, and Dongsheng Zhao [4, Theorem 4.1].

Let me remind you, from Section 8.2.1 in the book, that an irreducible closed subset of a space X is a closed subset C that is non-empty and such that if C is included in a union of two closed sets, then it must be included in one of them already. Equivalently, C is non-empty and given any two open sets U and V that C intersects, U ⋂ V also intersects C. Yet another equivalent definition is: C is irreducible if and only if for every finite family of open subsets of X that intersect C, their intersection also intersects C.

Every subset of the form ↓x is irreducible closed. A quasi-sober space is a space in which every irreducible closed is of the form ↓x for some point x, and a sober space is a T₀ quasi-sober space.

We rely on the following [4, Theorem 4.1].

Lemma I. In a first-countable ω-well-filtered topological space X, every irreducible closed subset C is directed in the specialization preordering.

Proof. Let (U^x_n)_{n ∈ N} be a countable base of open neighborhoods of each point x of C. Following Exercise 4.7.14 in the book, we will assume that they form a descending sequence U^x₀ ⊇ U^x₁ ⊇ … ⊇ U^x_n ⊇ …; the fact that they form a base of open neighborhoods means that every open neighborhood of x contains some U^x_n. (Yes, I have already said all this earlier in this post.)

C is non-empty, and it remains to show that given any two points x and y of C, there is a point z above x and y in C, in other words that ↑x ⋂ ↑y ⋂ C is non-empty.

Since x and y are in C, C intersects Ux0 and Uy0, and because C is irreducible, C must then intersect Ux0 ⋂ Uy0. Let z0 be a point in the intersection Ux0 ⋂ Uy0 ⋂ C. We now have three points in C, x, y and z0. Then C intersects Ux1, Uy1 and Uz01, so C intersects their intersection: let z1 be a point in the intersection Ux1 ⋂ Uy1 ⋂ Uz01 ⋂ C. We now have four points in C, x, y, z0 and z1. Then C intersects Ux2, Uy2, Uz02 and Uz12, so C intersects their intersection, and we then pick a point z2 be a point in the intersection Ux2 ⋂ Uy2 ⋂ Uz02 ⋂ Uz12 ⋂ C. We proceed this way forever, and we obtain points zk in Uxk ⋂ Uyk ⋂ Uz0k ⋂ … ⋂ Uzk–1k ⋂ C for every k ∈ N.

For every n ∈ N, let Kn ≝ {zn, zn+1, …}. We claim that Kn is compact. Let (Vi)i ∈ I be an open cover of Kn. Then zn is in Vi for some i ∈ I. By definition of (Uznm)m ∈ N as a base of open neighborhoods of zn, there is an index m ∈ N such that Uznm ⊆ Vi. For every k≥m, zk is in Uxk ⋂ Uyk ⋂ Uz0k ⋂ … ⋂ Uzk–1k ⋂ C, hence in Uznk. Since (Uznm)m ∈ N forms a descending sequence and k≥m, Uznk is included in Uznm, hence in Vi: therefore zk ∈ Vi for every k≥m. The remaining finitely many elements z0, z1, …, zk–1 are covered by finitely many sets Vj, j ∈ I, yielding a finite subcover of Kn.

Since K_n is compact, Q_n ≝ ↑K_n is compact saturated. It is clear that Q₀ ⊇ Q₁ ⊇ … ⊇ Q_n ⊇ … Let U be the complement of C. If ∩_{n ∈ N} Q_n were included in U, then some Q_n would be included in U, since we have assumed X ω-well-filtered; but this is impossible, since z_n ∈ K_n ⊆ Q_n and z_n is in C, hence not in U. Therefore ∩_{n ∈ N} Q_n is not included in U; equivalently, ∩_{n ∈ N} Q_n intersects C.

We pick a point z in the intersection ∩n ∈ N Qn ⋂ C. For every n ∈ N, z is in Qn, and is therefore above some point zk with k≥n. We recall that zk is in Uxk ⋂ Uyk ⋂ Uz0k ⋂ … ⋂ Uzk–1k ⋂ C, in particular in Uxk ⋂ Uyk. Since (Uxk)k ∈ N forms a descending sequence and k≥n, zk is also in Uxn, and since Uxn is upwards-closed and zk≤z, z is in Uxn. Similarly, z is in Uyn. This holds for every n ∈ N, so z ∈ ∩n ∈ N Uxn = ↑x and z ∈ ∩n ∈ N Uyn = ↑y. Since z is also in C, we have found the desired point of C above x and y. ☐

Every sober space is a monotone convergence space, namely a space that is a dcpo in its specialization ordering, and whose topology is coarser than the Scott topology of the specialization ordering (Proposition 8.2.34 in the book). This admits the following generalization to well-filtered spaces.

Lemma I. Every well-filtered T₀ space X is a monotone convergence space.

Proof. Let (x_i)_{i ∈ I} be a directed family in X. For each i ∈ I, let Q_i ≝ ↑x_i. Then (Q_i)_{i ∈ I} is a filtered family of compact saturated subsets. Let Q be its intersection. Let also C ≝ cl ({x_i | i ∈ I}) and U be the complement of C. If Q ⊆ U, then the fact that X is well-filtered implies that some Q_i is included in U; but that would imply x_i ∈ U, which is impossible. Therefore Q is not included in U, hence intersects C. Let x be a point in the intersection. Since x ∈ Q = ∩_{i ∈ I} Q_i = ∩_{i ∈ I} ↑x_i, x is an upper bound of (x_i)_{i ∈ I}. Given any other upper bound y, every open neighborhood U of x intersects C, hence {x_i | i ∈ I}, so U contains some x_i; because U is upwards-closed and x_i≤y, y is in U. We have just shown that every open neighborhood of x contains y, so x≤y. Since y is an arbitrary upper bound of (x_i)_{i ∈ I}, x is the least upper bound of (x_i)_{i ∈ I}.

It remains to show that every open subset U of X is Scott-open with respect to the specialization ordering ≤. U is upwards-closed, and given any directed family (x_i)_{i ∈ I}, with its supremum x in U, we claim that some x_i is in U. The point x is built as in the previous paragraph, and we have seen that any open neighborhood U of x intersects C, hence {x_i | i ∈ I}, so U contains some x_i; this concludes the proof. ☐

We conclude with the following, which is Corollary 3.13 of [2] or Theorem 4.2 of [4].

Theorem J. For a first-countable T₀ topological space X, the following are equivalent:

1. X is sober;
2. X is well-filtered;
3. X is an ω-well-filtered monotone convergence space;
4. X is a monotone convergence space and does not contain any Π⁰₂ subspace homeomorphic to S₁ or to S_D.

Proof. We already know that 1 ⇒ 2. 2 entails that X is ω-well-filtered, and a dcpo by Lemma I, so 2 ⇒ 3. 3 is equivalent to 4 by Theorem I.

Finally, we show that 3 ⇒ 1. Let X be ω-well-filtered, first-countable, T₀, and a monotone convergence space. By Lemma I, every irreducible closed subset C of X is directed. Since X is a monotone convergence space, C has a least upper bound x, and C is Scott-closed, so x ∈ C. In particular, ↓x ⊆ C. Since x is an upper bound of C, C ⊆ ↓x. Therefore C = ↓x and hence X is sober. ☐

1. Matthew de Brecht.  A generalization of a theorem of Hurewicz for quasi-Polish spaces. Logical Methods in Computer Science, 14(1:13)2018, pages 1–18, 2018; arXiv report 1711.09326.
2. Qingguo Li, Mengjie Jin, Hualin Miao, and Siheng Chen. On some results related to sober spaces. Acta Mathematica Scientia 43, pages 1477-1490, 2023.
3. Hualin Miao, Xiaodong Jia, Ao Shen, and Qingguo Li. ω-well-filtered spaces revisited. Houston Journal of Mathematics 50(2), pages 477-495, 2024.
4. Xiaoquan Xu, Chong Shen, Xiaoyong Xi, and Dongsheng Zhao, First countability, ω-well-filtered spaces and reflections, Topology and its Applications 279, 107255, 2020.

— Jean Goubault-Larrecq (February 20th, 2026)