Last time, we had started to study the maximal limit spaces, which are those spaces in which every net (equivalently, every proper filter) has either no limit at all, or a unique largest limit. The possibly pointed maximal limit spaces are the spaces in which every net has a unique largest limit. (A space is possibly pointed if and only if every net has a limit, if and only if it is empty or pointed. A pointed space is one with a least element in its specialization preordering.)
We will see that those kinds of spaces are preserved by various familiar constructions. The case of continuous function spaces will be by far the most sophisticated, and was dealt with by Hoover [1], along with liftings and the Smyth powerdomain.
For continuous functions, we will need a theorem (Theorem I) from the last post, and that relies on a notion called weak Hausdorffness; explicitly, one of the things that this theorem says is that a maximal limit space is the same thing as a weakly Hausdorff, coherent, sober space that is binary bounded-sup-complete in the sense that any two elements with an upper bound have a supremum with respect to the specialization ordering. A space X is weakly Hausdorff in the sense of Klaus Keimel and Jimmie Lawson [2] if and only if for any two points x and y in X, for every open neighborhood W of ↑x ∩ ↑y, there is an open neighborhood U of x and there is an open neighborhood V of y such that U ∩ V ⊆ W. We will also look at the preservation of weak Hausdorffness under familiar constructions.
Liftings
The lifting X⊥ of a topological space X is obtained by adding a fresh point ⊥, and by declaring that the open subsets of X⊥ are those of X, plus X⊥ itself. The specialization preordering of X⊥ coincides with that of X on pairs of elements of X, and puts ⊥ below all points.
Proposition A. X is a maximal limit space if and only if X⊥ is a (pointed) maximal limit space. X is weakly Hausdorff, resp. coherent, resp. sober, resp. binary bounded-sup-complete if and only if X⊥ is.
Proof. Let (xi)i ∈ I, ⊑ be any net in X⊥. This net has a limit, because ⊥ is a limit of every net. (The only open neighborhood of ⊥ is X⊥, and it certainly contains xi for i large enough.) Apart from ⊥, the limits of (xi)i ∈ I, ⊑ in X⊥ are exactly the points x in X such that every open neighborhood U of x in X⊥ contains xi for i large enough. Let J ≝ {i ∈ I | xi≠⊥}.
If J does not contain i for i large enough, namely if for every i in I there is a j⊒i such that xi=⊥, then by taking U≝X, we see that no point x of X can be a limit of (xi)i ∈ I, ⊑ in X⊥; in that case, the set of limits of (xi)i ∈ I, ⊑ in X⊥ is {⊥}, and that certainly has a unique largest element.
We now assume that J contains every large enough index in I: there is an index i0 in I such that for every i⊒i0, xi≠⊥. Then the limits of (xi)i ∈ I, ⊑ in X⊥ are (in addition to ⊥) exactly the points x in X such that every open neighborhood U of x in X (no longer X⊥) contains xi for i large enough (and larger than or equal to i0). Equivalently, the limits of (xi)i ∈ I, ⊑ in X⊥ are ⊥, plus all the limits of the subnet (xi)i ∈ J, ⊑ in X. The first part of the proposition then follows immediately.
If X is weakly Hausdorff, let x and y be any two points in X⊥ such that ↑x ∩ ↑y ⊆ W for some open subset of X⊥. We are looking for an open neighborhood U of x and an open neighborhood V of y in X⊥ such that U ∩ V ⊆ W. If x=⊥, then ↑x ∩ ↑y ⊆ W simplifies to y ∈ W, and we may take U≝X⊥, V≝W; similarly if y=⊥. If W is the whole of X⊥, we may take U≝V≝X⊥. If both x and y are in X and W is included in X, then we use the fact that X is weakly Hausdorff to find U and V. Hence X⊥ is weakly Hausdorff.
Conversely, if X⊥ is weakly Hausdorff, then given any two points x and y in X, and an open subset W of X that contains ↑x ∩ ↑y, there is an open neighborhood U of x and an open neighborhood V of y in X⊥ such that U ∩ V ⊆ W. Replacing U by its intersection with (the open set) X⊥ and similarly with Y establishes that X is weakly Hausdorff.
The part about coherence is proved as follows. By Exercise 4.4.26 in the book, the compact saturated subsets of X⊥ are those of X plus X⊥ itself. If X is coherent, then any two compact saturated subsets of the first form have compact saturated intersection, while intersecting one compact subset Q of X with X⊥ yields Q. Hence X⊥ is coherent. The converse is equally easy.
The part about sobriety is Exercise 8.2.9 in the book. The part about binary bounded-sup-complete is elementary. ☐
The second part of Proposition A gives us a second argument why a lifting of a maximal limit space is a maximal limit space: it is weakly Hausdorff, coherent, sober and binary bounded-sup-complete.
Products
The following is also pretty easy to see.
Proposition B. Any product of maximal limit spaces is a maximal limit space. (Same thing with possibly pointed spaces, hence with possibly pointed maximal limit spaces.)
Proof. Let X be the product of an arbitrary family of spaces Xi, i ∈ I. Given any net ((xji)i ∈ I)j ∈ J, ⊑ with a limit in X, the limits of that net are exactly the tuples (xi)i ∈ I where for each i ∈ I, xi is a limit of the net (xji)j ∈ J, ⊑. If there is a unique largest limit xi of (xji)j ∈ J, ⊑ in Xi for each i ∈ I, then collecting them into a tuple as (xi)i ∈ I must yield the largest limit of ((xji)i ∈ I)j ∈ J, ⊑ in X.
For possibly pointed spaces, either one term in the product is empty and the product is empty, or all spaces are pointed, and then the product is clearly pointed. ☐
Conversely, and using a similar argument, if the product X of the spaces Xi, i ∈ I, is a maximal limit space and if each Xi is non-empty, then each Xi is a maximal limit space: given any net (yj)j ∈ J, ⊑ in Xi, we pick an element zi’ from each Xi’ with i’≠i, and we form the net ((xji)i ∈ I)j ∈ J, ⊑ in X by letting xji ≝ yj and xji’ ≝ zi’ for every i’≠i. If (yj)j ∈ J, ⊑ has a limit y in in Xi, then ((xji)i ∈ I)j ∈ J, ⊑ also has a limit in X, and then it has a unique largest limit, whose ith component must be the unique largest limit of (yj)j ∈ J, ⊑.
Corollary C. The space YX of all functions from a set X to a maximal limit space Y is maximal limit space in the topology of pointwise convergence (defined as the product topology on the product YX). Also, YX is possibly pointed if Y is.
Spaces of monotone functions
Let us now require that X be a preordered set, or a topological space, understood with its specialization preordering. We also equip Y with its specialization preordering. Inside YX, we find the subspace (X → Y)mon of monotonic maps. Then we have the following.
Lemma D. Let X and Y be topological spaces, and let us assume that Y is T0. The maximal limit f of a net (fi)i ∈ I, ⊑ of monotonic maps from X to Y, taken in YX (with the topology of pointwise convergence), if it exists, is monotonic.
Proof. Let us fix any two points x and y such that x≤y in X. We define a new function g from X to Y by g(y) ≝ f(x), and for every z≠y, g(z) ≝ f(z). (There is no requirement of continuity on those functions, so that definition is fine.) We claim that g is also a limit of (fi)i ∈ I, ⊑. We need to show that for every open neighborhood W of g, fi is in W for i large enough. By Exercise 4.7.29 in the book, it suffices to check this when W is taken from any given subbase of the topology. By definition of the topology of pointwise convergence (i.e., the product topology), a subbase is given by the sets [z ∈ V], defined as {h : X → Y | h(z) ∈ V}, where z ranges over the points of X and V ranges over the open subsets of Y. Now, if g is in [z ∈ V],
- either z≠y, and f(z) ∈ V, so fi(z) is in V for i large enough, since f is a limit of (fi)i ∈ I, ⊑ in YX, and this shows that fi is in [z ∈ V] for i large enough;
- or z=y, and f(x) ∈ V; in that case, fi(x) is in V for i large enough, since f is a limit of (fi)i ∈ I, ⊑ in YX; since fi is monotonic, x≤y and V is upwards-closed, fi(y) is also in V for i large enough; namely, fi is in [z ∈ V] for i large enough, as in the previous case.
Right, so g is a limit of (fi)i ∈ I, ⊑. But f is the largest one, so g≤f. In particular, g(y)≤f(y), and by definition this means f(x)≤f(y). This holds for any pair of points x and y such that x≤y, so f is indeed monotonic. ☐
Corollary E. For every topological space X, for every (resp., possibly pointed) maximal limit space Y, (X → Y)mon is a (resp., possibly pointed) maximal limit space, and maximal limits are computed as in the superspace YX, namely, pointwise.
Proof. First, if Y is possibly pointed, then so is (X → Y)mon: either Y is empty and the case is trivial, or Y has a least element ⊥ and the constant ⊥ map is monotonic, hence the least element of (X → Y)mon.
For every net (fi)i ∈ I, ⊑ that has a limit g in (X → Y)mon, g is also a limit of the same net in YX. This is because we have defined (X → Y)mon as a topological subspace of YX. Since Y is maximal limit space, (fi)i ∈ I, ⊑ has a unique largest limit f in YX, and f is in (X → Y)mon by Lemma D. (Oh, Lemma D applies, because every maximal limit space is T0. You can deduce from the fact that every maximal limit space is sober. You can also prove it by hand: any constant net (x)i ∈ I, ⊑ has a unique largest limit, and its set of limits is ↓x—I will let you conclude.) Then f is also a limit of (fi)i ∈ I, ⊑ in (X → Y)mon, since (X → Y)mon is a topological subspace of YX, and for every other limit f’ of (fi)i ∈ I, ⊑ in (X → Y)mon, f’ is a limit of (fi)i ∈ I, ⊑ in YX, so f’≤f. ☐
Retracts
In the situation where we have two spaces X and Y, a continuous map s : X → Y and a continuous map r : Y → X such that r o s = idX, we say that X is a retract of Y, with retraction r and section s. Quite a number of properties are closed under retracts, in the sense that if Y has such a property, then X has it, too: T0-ness (Lemma 4.10.32 in the book), sobriety (Exercise 8.2.43), being a monotone convergence space (Exercise 8.2.40), local compactness and compactness (Proposition 4.10.33), well-filteredness, coherence, stable local compactness and stable compactness (Proposition 9.2.3), Noetherianness (Proposition 9.7.18 (v)), etc.
Proposition F. Any retract X of a maximal limit space Y is a maximal limit space. Writing r for the retraction and s for the section, the unique largest limit of a convergent net (xi)i ∈ I, ⊑ in X is equal to r(y), where y is the unique largest limit of (s(xi))i ∈ I, ⊑ in Y.
Proof. We will use the fact that a continuous map is the same thing as a map that preserves limits (Proposition 4.7.18 in the book). Since (xi)i ∈ I, ⊑ converges in X, (s(xi))i ∈ I, ⊑ is a convergent net in Y. Since Y is a maximal limit space, that net has a unique largest limit y. Then r(y) is a limit of (r(s(xi)))i ∈ I, ⊑, that is, of (xi)i ∈ I, ⊑ since r o s = idX.
Let x be any limit of (xi)i ∈ I, ⊑ in X. Then s(x) is a limit of (s(xi))i ∈ I, ⊑ in Y. Since y is the largest, s(x) ≤ y. Now every continuous map is monotonic, so r(s(x)) ≤ r(y), or equivalently, x ≤ r(y). This shows that r(y) is a largest limit of (xi)i ∈ I, ⊑ in X. But Y is T0, so X is T0, too, and therefore it is its unique largest limit. ☐
Another proof is obtained by showing that retractions preserve weak Hausdorffness, coherence, sobriety and binary bounded-sup-completeness. For coherence and sobriety, I have already said so above.
Proposition G. Every retract of a weakly Hausdorff space is weakly Hausdorff. Every retract of a binary bounded-sup-complete space is binary bounded-sup-complete.
Proof. We reuse the notation r, s, X, Y (with Y weakly Hausdorff). Let x and x’ be two points in X, and W be an open subset of X that contains ↑x ∩ ↑x’. Then ↑s(x) ∩ ↑s(x’) is included in r–1(W): for every y ∈ ↑s(x) ∩ ↑s(x’), we have s(x) ≤ y, hence x=r(s(x)) ≤ r(y) and similarly x’ ≤ r(y); so r(y) is in ↑x ∩ ↑x’, hence in W. We use the fact that Y is weakly Hausdorff, and we find an open neighborhood U of s(x) in Y and an open neighborhood V of s(x’) in Y such that U ∩ V ⊆ r–1(W). Then s–1(U) is an open neighborhood of x in X, s–1(V) is an open neighborhood of x’ in X, and s–1(U) ∩ s–1(V) ⊆ W: for every point z in s–1(U) ∩ s–1(V), s(z) is both in U and in V, hence is in r–1(W), and therefore z = r(s(z)) is in W.
For binary bounded-sup-completeness, let x and x’ be two points with an upper bound z in X. Then s(x) and s(x’) have s(z) as upper bounds in Y, so if Y is binary bounded-sup-complete, then s(x) and s(x’) have a least upper bound y in Y. We now verify that r(y) is a least upper bound of x and x’ in X: we have x = r(s(x)) ≤ r(y), and similarly x’ ≤ r(y), so r(y) is an upper bound of x and x’ in X; if x” is any other upper bound of x and x’, then s(x”) is an upper bound of s(x) and s(x’) in Y, so y ≤ s(x”), and by applying r we obtain that r(y) ≤ r(s(x”)) = x”. ☐
Continuous function spaces
We write [X → Y] for the space of continuous maps from X to Y. We will write [X → Y]⊚ for [X → Y] with the core-open topology, whose subbasic open subsets are the sets [U ⋐–1 V] of continuous maps f : X → Y such that U ⋐ f–1(V) (Definition 5.4.1 in the book); ⋐ is the way-below relation on the collection OX of open subsets of X. This mostly makes sense when X is core-compact, namely when OX is a continuous complete lattice, in which case the core-open topology is the unique exponential topology (Theorem 5.4.4 in the book). Hoover considers the compact-open topology on [X → Y], in the case where X is locally compact, but in that case, the compact-open and core-open topologies coincide (Exercise 5.4.8 in the book).
We will need the following later on.
Fact H. For every core-compact space X, for every space Y, the specialization preordering of [X → Y]⊚ is the pointwise preordering: f≤g if and only if f(x)≤g(x) for every x ∈ X.
Proof. Clearly, if f is pointwise below g and in [U ⋐–1 V], then g is also in [U ⋐–1 V]: every point of U is included in f–1(V), and f–1(V) is included in g–1(V) because V is upwards-closed. If f is not pointwise below g, then there is a point x ∈ X such that f(x)≰g(x). By definition of the specialization preordering on Y, there is an open subset V of X that contains f(x) but not g(x). Then x is in f–1(V). Since X is core-compact, there is an open neighborhood U of x such that U ⋐ f–1(V). Then f is in [U ⋐–1 V]. But g is not, since x is in U but not in g–1(V). Therefore f is not below g in the specialization preordering of [X → Y]⊚. ☐
The question whether [X → Y]⊚ is a maximal limit space is a lot more complicated than with products and retracts. Hoover proved that it is, provided that X is locally compact and Y is a maximal limit space [1, Theorem 5.3 (iii)]. We will consider the case where X is core-compact, but that is only a very minor generalization.
This is one case where reasoning from the definition of possibly pointed maximal limit spaces, using nets, would lead us nowhere, most likely. (I tried, although not very hard.) We will need to use the characterization I have already alluded to, and which is Theorem I of the last post. One part of this theorem is that the maximal limit spaces are exactly the weakly Hausdorff, binary bounded-sup-complete, monotone convergence spaces. A monotone convergence space is a T0 space in which all directed suprema exist, and in which every open set is Scott-open (with respect to the specialization ordering), and we start with that property.
The level of generality at which the following lemma is stated exceeds what Hoover does, and was suggested by Xiaodong Jia.
Lemma I. Let X be a topological space, Y be a monotone convergence space. With any topology whose specialization ordering is the pointwise ordering ≤ and that is coarser than the Scott topology of ≤, [X → Y] is a monotone convergence space. Additionally, suprema of directed families (fi)i ∈ I of continuous functions are computed pointwise.
In particular, if X is core-compact, then [X → Y]⊚ is a monotone convergence space.
Proof. Let (fi)i ∈ I, ⊑ be any monotone net in [X → Y]. (Any monotone net induces a directed family (fi)i ∈ I, and conversely any directed family (fi)i ∈ I induces a monotone net (fi)i ∈ I, ⊑ provided that we define i ⊑ j if and only if fi≤fj.) We define f as its pointwise supremum, namely by f(x) ≝ supi ∈ I fi(x) for every x in X.
We will use the fact that for every open subset V of Y, f–1(V) is the directed union of the sets fi–1(V). That is directed because i ⊑ j implies fi≤fj, hence fi–1(V) ⊆ fi–1(V), since V is upwards-closed. Similarly, fi–1(V) ⊆ f–1(V) for every i in I, and it remains to show that f–1(V) is included in ∪i ∈ I fi–1(V). For every x ∈ f–1(V), f(x), which is equal to the directed supremum of the values fi(x), and is in V, which is open hence Scott-open by assumption. Therefore fi(x) ∈ V for some i ∈ I.
Let x ∈ X and V be an open neighborhood of f(x). Then x ∈ f–1(V) = ∪i ∈ I fi–1(V), so there is an index i ∈ I such that x ∈ fi–1(V). Let U ≝ fi–1(V). This is an open neighborhood of x in X, and U = fi–1(V) ⊆ f–1(V), as we have seen in the previous paragraph. Therefore f is continuous at x. Since x is arbitrary, f is continuous. It follows that f is the least upper bound of (fi)i ∈ I, ⊑ in [X → Y].
Together with the fact that the topology on [X → Y] is coarser than the Scott topology of the pointwise ordering, this shows that [X → Y] is a monotone convergence space.
We apply this to [X → Y]⊚. When X is core-compact, Fact H tells us that its specialization ordering is the pointwise ordering ≤. In order to apply the above and conclude, it remains to show that the topology of [X → Y]⊚ is coarser than the Scott topology. To this end, we only need to show that every subbasic open subset [U ⋐–1 V] (U open in X, V open in Y) is Scott-open. Let (fi)i ∈ I, ⊑ and f be as above, and let us assume that f is in [U ⋐–1 V]. Then U ⋐ f–1(V). Because X is core-compact, we can use interpolation on OX (Proposition 5.1.15 in the book): there is open set U’ such that U ⋐ U’ ⋐ f–1(V). Therefore U’ ⋐ f–1(V) = ∪i ∈ I fi–1(V). From the definition of the way-below relation ⋐, U’ ⊆ fi–1(V) for some i ∈ I, so U ⋐ fi–1(V). In other words, fi is in [U ⋐–1 V]. ☐
We now proceed with the weakly Hausdorff and binary bounded-sup-complete part. It seems like we have to deal with both at the same time.
Proposition J. If X is core-compact and Y is a binary bounded-sup-complete weakly Hausdorff space, then [X → Y]⊚ is binary bounded-sup-complete, and binary suprema of bounded pairs are computed pointwise; also, [X → Y]⊚ is weakly Hausdorff.
Proof. Let f, g be two elements of [X → Y]⊚ with a common upper bound. We form the pointwise supremum h of f and g, which exists because Y is binary bounded-sup-complete. We claim that h is continuous. Let x be an arbitrary point in X, and let W be an open neighborhood of h(x). Then ↑h(x) is included in W, and by definition of h as a supremum, ↑h(x) is equal to ↑f(x) ∩ ↑g(x). Since Y is weakly Hausdorff, there is an open neighborhood U of f(x) and there is an open neighborhood V of g(x) such that U ∩ V ⊆ W. Then f–1(U) ∩ g–1(V) is an open neighborhood of x. Since f≤h, we have f–1(U) ⊆ h–1(U), and similarly g–1(V) ⊆ h–1(V), so f–1(U) ∩ g–1(V) ⊆ h–1(U) ∩ h–1(V) = h–1(U ∩ V) ⊆ h–1(W). Therefore h–1(W) is an open neighborhood of x, too, and this shows that h is continuous. It is then clear that h is the least upper bound of f and g with respect to the pointwise ordering, hence in [X → Y]⊚.
We now show that [X → Y]⊚ is weakly Hausdorff. This is the more technical part. Since [X → Y]⊚ is binary bounded-sup-complete, the claim simplifies to: for any two elements f, g of [X → Y]⊚ with an upper bound, and letting h be their supremum, every open neighborhood W of h in [X → Y]⊚ must contain an intersection U ∩ V of an open neighborhood of f and an open neighborhood of g.
Since h ∈ W, h must be in a finite intersection ∩j=1n [Sj ⋐–1 Wj] of subbasic open sets, that intersection being included in W. (Each Sj is open in X and each Wj is open in Y.) We will show that each of the sets [Sj ⋐–1 Wj] contains an intersection Uj ∩ Vj of open subsets of [X → Y]⊚, where f ∈ Uj and g ∈ Vj, for each j, 1≤j≤n. It will follow that f ∈ ∩j=1n Uj, g ∈ ∩j=1n Vj, and the intersection of ∩j=1n Uj with ∩j=1n Vj is included in W. We henceforth fix an index j.
For the purpose of illustration, one may imagine that the situation is as follows. Here n=2, the space X is on the left, Y is on the right, and we have shown prototypical instances of S1, S2, and W1 and W2. When we continue this example, we will always imagine that the fixed index j is 1.
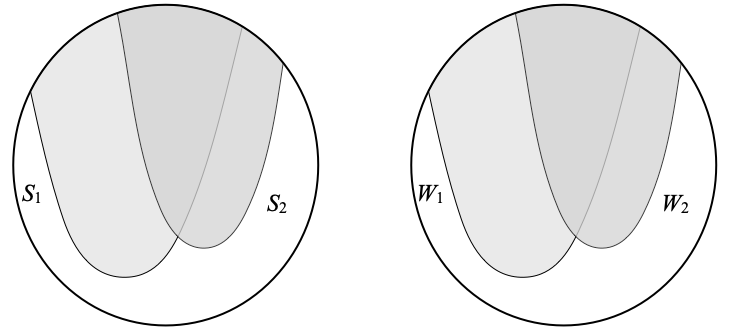
Continuing with the example, f maps every point x on the left to a point f(x) on the right, similarly with g, and h(x) is above both f(x) and g(x). If we start from a point x inside S1, then h is in [Sj ⋐–1 Wj], h(x) must be in W1:
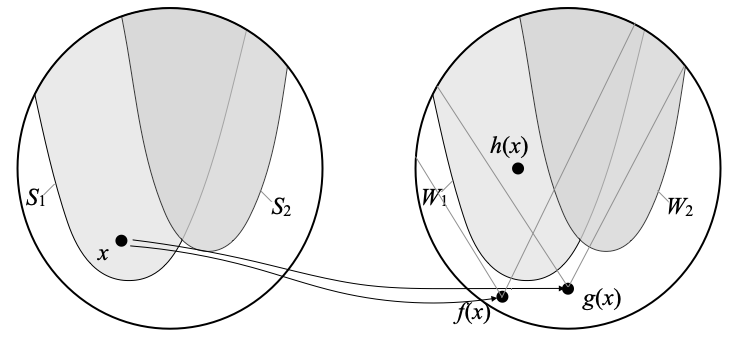
- Since h is in [Sj ⋐–1 Wj], Sj ⋐ h–1(Wj). Using interpolation in the continuous dcpo OX (since X is core-compact), there is an open set Tj such that Sj ⋐ Tj ⋐ h–1(Wj). We are now in the following situation:
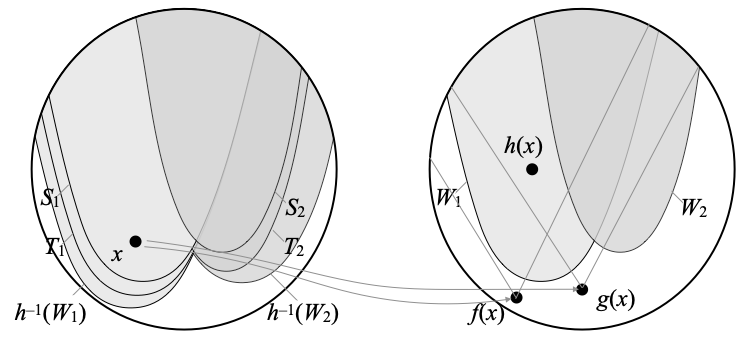
- For every x ∈ h–1(Wj), h(x) is in Wj, so ↑f(x) ∩ ↑g(x) is included in Wj. Since Y is weakly Hausdorff, there is an open neighborhood Uj,x of f(x) and there is an open neighborhood Vj,x of g(x) such that Uj,x ∩ Vj,x ⊆ Wj. In our example, with j=1, this can be depicted as follows:
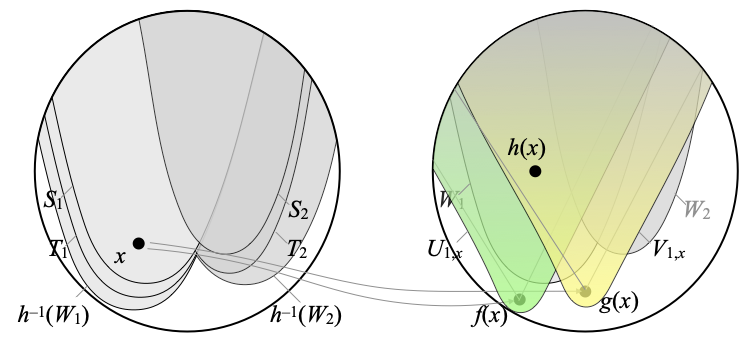
- Since f is continuous, f–1(Uj,x) is open. Similarly, g–1(Vj,x) is open, and both contain x. Using the fact that X is core-compact, there is an open neighborhood Sj,x of x such that Sj,x ⋐ f–1(Uj,x) ∩ g–1(Vj,x) (this is Proposition 5.2.6 in the book). In our example, with j=1, we obtain the following new set on the left:
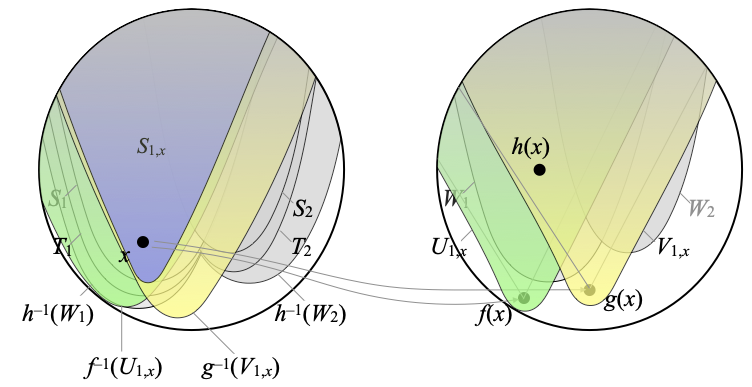
- The sets Sj,x are defined for every x ∈ h–1(Wj), and therefore form an open cover of h–1(Wj). Writing the union ∪x ∈ h–1(Wj) Sj,x as a directed union of finite unions (Trick 4.4.6 in the book), and using the fact that Tj ⋐ h–1(Wj), Tj is included in some finite union ∪x ∈ E Sj,x (where the indexing set E is a finite subset of h–1(Wj), hence).
- We define Uj as the finite intersection ∩x ∈ E [Sj,x ⋐–1 Uj,x], and Vj as ∩x ∈ E [Sj,x ⋐–1 Vj,x]. Since Sj,x ⋐ f–1(Uj,x) ∩ g–1(Vj,x) ⊆ f–1(Uj,x) for every x ∈ h–1(Wj), in particular for every x ∈ E, f is in Uj, and similarly g is in Vj.
- It remains to show that Uj ∩ Vj ⊆ [Sj ⋐–1 Wj]. For every element h’ of Uj ∩ Vj, we wish to show that Sj ⋐ h’–1(Wj). Since Sj ⋐ Tj, it suffices to show that Tj ⊆ h’–1(Wj). We consider any point z in Tj. Since Tj ⊆ ∪x ∈ E Sj,x, there is an element x of E such that z ∈ Sj,x. Since h’ ∈ Uj ∩ Vj, h’ is in particular in [Sj,x ⋐–1 Uj,x] and in [Sj,x ⋐–1 Vj,x], so h’(z) is both in Uj,x and in Vj,x. We recall that Uj,x ∩ Vj,x ⊆ Wj, so h’(z) is in Wj. We had chosen z arbitrary in Tj, so Tj ⊆ h’–1(Wj), as promised. ☐
We can now combine Lemma I and Proposition J, using Theorem I of the last post, and we obtain Hoover’s theorem.
Theorem K. For every core-compact space X, for every maximal limit space Y, [X → Y]⊚ is maximal limit space. It is possibly pointed if Y is.
Proof. Item 4 of Theorem I of the last post tells us that the maximal limit spaces are exactly the weakly Hausdorff, binary bounded-sup-complete, monotone convergence spaces. Hence both Lemma I and Proposition J apply. Lemma I tells us that [X → Y]⊚ is a monotone convergence space, Proposition J tells us that [X → Y]⊚ is binary bounded-sup-complete and weakly Hausdorff. Therefore it is a maximal limit space.
By Lemma D, item 4 of the last post, a space is possibly pointed if and only if it is empty or has a least element. If Y is empty, then either X is empty and then [X → Y]⊚ contains just one function, which is therefore least, or X is non-empty and then [X → Y]⊚ is empty. If Y is non-empty, then it has a least element ⊥, and then the constant function with value ⊥ is the least element of [X → Y]⊚. ☐
The Smyth hyperspace
The Smyth hyperspace QX of a space X is the space of all compact saturated subsets of X, with the upper Vietoris topology: its basic open subsets are of the form ☐U ≝ {Q ∈ Q(X) | Q ⊆ U}, where U ranges over the open subsets of X. QX is a T0 space, whose specialization ordering is reverse inclusion. There is a variant of this construction, where we only take the non-empty compact saturated subsets of X, and I will sometimes comment on that.
We need the following fact to A. Schalk [4, Lemma 7.20]. We will need to observe that ☐ commutes with binary intersections, and with directed unions, too: for any directed family (Ui)i ∈ I of open subsets of X, for every Q ∈ Q(X), Q is in ☐∪i ∈ I Ui if and only if Q is in some Ui (by compactness), if and only if Q is in ∪i ∈ I ☐Ui.
Lemma L. For every sober space X, QX is sober.
Proof. Let C be an irreducible closed subset of QX. Let F be the collection of open subsets U of X such that ☐Uintersects C. F contains X, is upwards-closed, and even Scott-open: for any directed family (Ui)i ∈ I of open subsets of X, if ☐∪i ∈ I Ui intersects F, namely if ∪i ∈ I ☐Ui intersects F, then some ☐Ui intersects F. Finally, F is a filter: since C is irreducible, if it intersects ☐U and ☐V, then it intersects ☐U ∩ ☐V = ☐(U ∩ V).
Therefore F is a Scott-open filter of open subsets of X. By the Hofmann-Mislove theorem (Theorem 8.3.2 in the book), F is exactly the collection of open neighborhoods of some compact saturated subset Q of X. (If we had defined QX as the space of all non-empty compact saturated subsets, we need to check that Q is non-empty: in that case, otherwise, F would contain the empty set, so ☐∅ would intersect C, but ☐∅ is empty.) For every element Q’ of C, by definition of F, every open neighborhood of Q’ is in F, hence contains Q; it follows that C is included in the upward closure ↑QXQ of Q in QX. In order to see that C is equal to ↑QXQ (which we finish our proof that QX is sober), it suffices to show that Q is in C. If Q were not in C, it would be in its complement, which is open, hence equal to a union ∪i ∈ I ☐Ui of basic open sets. Then Q is included in some Ui, and then ☐Ui is included in the complement of C, so by definition Ui is not in F. But Ui is in F, since Ui contains Q. Therefore we reach a contradiction, and we conclude. ☐
We now make an observation that is due to Keimel and Lawson [2, Lemma 6.6]. No proof of it is given there, except for an appeal to “a standard compactness argument”.
Lemma M. A space X is weakly Hausdorff if and only if for every pair of compact saturated subsets Q and Q’ of X, for every open neighborhood W of Q ∩ Q’, there is an open neighborhood U of Q and an open neighborhood V of Q’ such that U ∩ V is included in W.
Proof. The if direction is clear: just take Q to be the upward closure of a point, as well as Q’.
Conversely, we proceed in two steps. Let us assume X weakly Hausdorff, let Q be a compact saturated subset of X, y be a point of X, and let W be an open neighborhood of Q ∩ ↑y: we show that there is an open neighborhood U of Q, and an open neighborhood V of y such that U ∩ V ⊆ W. For every x in Q, by assumption there is an open neighborhood Ux of xand an open neighborhood Vx of y such that Ux ∩ Vx is included in W. Since Q is compact, it is covered by finitely many sets Ux, say for x varying in a finite set E. We let U ≝ ∪x ∈ E Ux, V ≝ ∩x ∈ E Vx, and then U ∩ V ⊆ ∪x ∈ E (Ux ∩ Vx) ⊆ W.
Next, let Q and Q’ be two compact saturated subsets of X and W be an open neighborhood of Q ∩ Q’. For every y in Q’, we have just shown that there is an open neighborhood Uy of Q and an open neighborhood Vy of y such that Uy ∩ Vy is included in W. Since Q’ is compact, it is covered by finitely many sets Vy, say for y varying in a finite set E. We let U ≝ ∩y ∈ E Uy, V ≝ ∪y ∈ E Vy, and then U ∩ V ⊆ ∪y ∈ E (Uy ∩ Vy) ⊆ W. ☐
We recall from this post on weakly Hausdorff spaces and locally strongly sober spaces that the locally strongly sober spaces are exactly the weakly Hausdorff, coherent, sober spaces. The maximal limit spaces are those locally strongly sober spaces that are bounded-sup-complete.
Theorem N. For every locally strongly sober space X, QX is a maximal limit space.
Proof. Let us start this by showing that QX is weakly Hausdorff. Let Q and Q’ be two elements of QX, and let W be an open neighborhood of ↑QXQ ∩ ↑QXQ’, where ↑QX denotes upward closure in QX. In other words, W contains every compact saturated set that is included in Q and in Q’, or equivalently W contains the compact saturated set Q ∩ Q’. We write W as ∪i ∈ I ☐Wi, where each Wi is open in X. Then Q ∩ Q’ ⊆ Wi for some i in I, and by Lemma M, there is an open neighborhood U of Q and an open neighborhood V of Q’ such that U ∩ V is included in Wi. Therefore Q is in ☐U, so that ↑QXQ ⊆ ☐U; similarly, ↑QXQ’ ⊆ ☐V; and ☐U ∩ ☐V = ☐(U ∩ V) ⊆ ☐Wi ⊆ W. This shows that QX is weakly Hausdorff. (If we considered the collection of non-empty saturated subsets of X for QX, we would have to modify this argument and consider the case where Q ∩ Q’ is empty. Then the same argument would hold with the empty set in place of Wi: U ∩ V would then be empty, and then ☐U ∩ ☐V = ☐(U ∩ V) = ∅ ⊆ W.)
Since X is sober, QX is sober by Lemma L. In particular, it is a monotone convergence space (see Proposition 8.2.34 in the book).
Since X is coherent, QX is bounded-sup-complete: given any two compact saturated subsets Q and Q’ of X, Q ∩ Q’ is their least upper bound. (If we considered the collection of non-empty saturated subsets of X for QX, we would have to modify this argument and say: if Q and Q’ have an upper bound, then Q ∩ Q’ is non-empty, and must therefore be their least upper bound.)
Finally, by Theorem I of the last post, the maximal limit spaces are exactly the weakly Hausdorff, binary bounded-sup-complete, monotone convergence spaces, so QX is a maximal limit space. ☐
The Hoare hyperspace
The Hoare hyperspace HX is the set of all closed subsets of X, with the lower Vietoris topology, whose subbasic open sets are ♢U ≝ {F ∈ HX | F ∩ U ≠ ∅}, where U ranges over the open subsets of X. (There is also a variant where we only consider the non-empty closed subsets of X.) The lower Vietoris topology is the same thing as the upper topology on HX, namely the coarsest topology such that the the downward closure ↓HX F of any element F is closed. Indeed, writing U for the complement of F, the complement of ↓HX F is ♢U. (In general, the upper topology on a poset is the coarsest one that makes every downward closure of a point closed. I write ↓HX for downward closure in HX.)
Schalk showed that HX is always sober. In fact, she showed the following more general statement [4, Proposition 1.7]: every poset P in which every non-empty family has a supremum is sober in its upper topology. We have already seen this in this post. HX is also a sup-semi-lattice, namely a poset in which any two elements have a least upper bound.
Theorem O. Every sup-semi-lattice P is a maximal limit space when equipped with its upper topology. In particular, HX is a maximal limit space for every topological space X.
Proof. We show that P is weakly Hausdorff first. Let x and y be two points of P, and let us assume that ↑x ∩ ↑y is included in some open subset W. By definition of the upper topology, the complement of W is an intersection ∩i ∈ I ↓Ei, where each Ei is a finite set. (And if ↓Ei={u1, …, un}, then ↓Ei is the union of ↓u1, …, ↓un.) We are looking for an open neighborhood U of x and an open neighborhood V of y such that U ∩ V ⊆ W.
For this, we consider the least upper bound z of x and y. Since z is in ↑x ∩ ↑y, it is in W, hence it is outside some ↓Ei. Let A be the collection of points u of Ei such that x ≰ u, and B be the collection of points u of Ei such that y ≰ u. Then Ei = A ∪ B: for every point u of Ei, z ≰ u since z is not in ↓Ei, and that implies that x ≰ u or y ≰ u, since otherwise x ≤ u and y ≤ u would entails z ≤ u. Let U be the complement of ↓A and V be the complement of ↓B. Then U∩ V is the complement of ↓A ∪ ↓B = ↓(A ∪ B) = ↓Ei, so U ∩ V ⊆ W. Also, x is in U: otherwise we would have x ≤ ufor some u ∈ A, which is impossible by definition of A; and similarly y is in V.
Right, so P is weakly Hausdorff. By Schalk’s theorem, it is sober, hence a monotone convergence space. Being a sup-semi-lattice, it is binary bounded-sup-complete, so by Theorem I of the last post (once again!), HX is a maximal limit space. (And this applies whether we consider the set of all closed subsets of X, or just the non-empty closed subsets, for HX.) ☐
- Douglas N. Hoover. Maximal Limit Spaces, Powerspaces, and Scott Domains. Proceedings of the 11th International Conference on Mathematical Foundations of Programming Semantics (MFPS), New Orleans, Louisiana, USA. Electronic Notes in Theoretical Computer Science 1:253–272, 1995.
- Klaus Keimel and Jimmie Lawson. Measure extension theorems for T0-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
- Jean Goubault-Larrecq. On weakly Hausdorff spaces and locally strongly sober spaces. Topology Proceedings, 62:117–131, Oct. 2023, available as arXiv report 2211.10400.
- Andrea Schalk. Algebras for Generalized Power Constructions. PhD thesis, Technische Hochschule Darmstadt, 1993. Available from http://www.cs.man.ac.uk/~schalk/publ/diss.ps.gz.

— Jean Goubault-Larrecq (April 20th, 2024)
